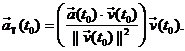|
F 3/1/13
|
HW due:
1. Read §10-4.
2. Work through the related rates tutorial.
As you work through the 3 illustrative examples (balloon problem, ladder problem,
and watch problem), make a sketch for each one. Go through the steps, showing
the work on your own HW paper, and make sure that you obtain the same answers
as those that are given.
3. Work through these 2
practice problems.
|
|
|
M 3/4/13
|
HW due: Sleep! Also, patch
up the missing holes in your previously assigned problems. Use of a
spreadsheet for the subway problem is strongly recommended.
|
|
|
T 3/5/13
|
HW due: Read §10-5 (the “drowning
swimmer” problems); write §10-5 #3, 4, 5, 6.
|
|
|
W 3/6/13
|
No school (snow day).
|
|
|
Th
3/7/13
|
Note:
Please be prepared to log up to 70 minutes, since you have 2 full days to work
and a lot of extra time. Two 35-minute sessions are better than a single
70-minute session, if you have a choice.
HW due:
1. Read §10-7 on vectors. There is nothing to read in §10-6.
2. If you have not already done so, finish §10-5 #6 (working with a friend if
necessary, but not copying verbatim).
3. Write §10-6 #1, 2, 3, 6, 7, 10.
4. Become familiar with the following notational conventions:
(a) We will generally write <a, b> instead of the bulkier, clunkier (but equivalent) form, namely 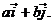 Feel free to use the
“angle bracket” notation in all of your questions and answers involving
vectors. Feel free to use the
“angle bracket” notation in all of your questions and answers involving
vectors.
(b) We will use the “double bar” notation for the norm of a vector. That
means that instead of writing 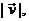 or |v|, we will write or |v|, we will write 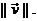
(c) Observe that the notations in (a) and (b) can be combined. For example,
we would say ||<3, 5>|| = 
5. Let 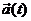 be the vector
function describing a particle’s acceleration, and let be the vector
function describing a particle’s acceleration, and let 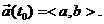 Similarly, let Similarly, let 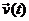 be the vector
function describing the same particle’s velocity, and let be the vector
function describing the same particle’s velocity, and let 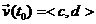 . .
(a) Prove that at time t = t0, the tangential
component of the acceleration vector is given by the formula
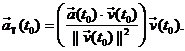
Note: The messy expression in the
large parentheses is a scalar, and
it is being used to multiply the velocity vector.
(b) After you have tried part (a), and regardless of whether or not you were
successful, take (a) as a given and prove the much easier formula
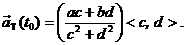
|
|
|
F 3/8/13
|
HW due: Write §10-7 #1, 9,
10, 11, 13, 14. There are several odd-numbered problems here so that you can
check your work.
Important: For maximum learning
benefit, try to solve the problems before checking answers in the back of the
book. Make a thorough try, including looking back through the section. Don’t
peek at the answers unless you and your study friend are both gridlocked with
no clue on how to proceed. Both here and on the AP exam, you are allowed to
use the formulas from the last problem in yesterday’s HW assignment without
reproving them. Another formula you can use without proof is
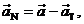
which is an immediate consequence of the fact that when we decompose 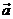 into components into components 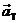 and and 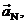 we insist that we insist that 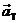 and and 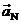 must add up to equal must add up to equal
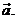
|
|
|
M 3/11/13
|
HW due:
1. Finish all previously assigned problems, especially §10-7 #14. Hint: Use the Law of Cosines.
2. Write §11-2 #3, 4. If you attend the NSO
competition at the Kennedy Center at 7:30 p.m. on Sunday, March 10, you
are exempt from having to do these last two problems. Good luck, Sam!!
|
|
|
T 3/12/13
|
HW due: Read §11-3; write
§11-2 #5, 6, 7.
|
|
|
W 3/13/13
|
HW due: Read §11-6; write
§11-3 #6, 7, 12, and the additional problem listed below. Note: We are skipping §§11-4 and 11-5.
Additional problem:
Use “cubical shells” to prove that the volume of a cube is e3, where e = edge length. Build this up from
the fact that the surface area of a cube is 6e2.
|
|
|
Th 3/14/13
|
HW due: Read §12-1; write
§12-1 #1-7 all.
|
|
|
F 3/15/13
|
HW due: Read §12-2; write
§12-2 #1, 2, 3, 8, 9.
|
|
|
M 3/18/13
|
HW due: Read §12-3; write
§12-3 #1-11 all.
|
|
|
T 3/19/13
|
HW due: Correct the February test to 100% accuracy. Additional
instructions are listed below.
1. This assignment is required of everyone, even students who did relatively
well. Nobody had a perfect score.
2. If you write on your existing test paper, use a different color of ink
(not red) so that the original and your corrections are clearly
distinguishable.
3. There are no restrictions on the help you seek. However, (1) you must list
the names of any people who helped you, and (2) the problem writeups are
still required to be legible and complete, in your own handwriting.
4. Corrections that are done especially well will qualify for additional
points. Mr. Hansen is dedicated to helping all students learn and succeed
(yes, this is actually true), and incentives that promote learning are, in
general, a good thing. Thank you to the student who made this suggestion.
Important additional note: Several
students forgot to turn in yesterday’s pop quiz so that it could be recorded.
If you wish to have your score recorded, please submit your quiz sheet.
|
|
|
W 3/20/13
|
HW due: Prove by any means
at your disposal (other than copying and pasting) that 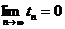 is a necessary but
not sufficient condition for the series consisting of terms ti to converge. is a necessary but
not sufficient condition for the series consisting of terms ti to converge.
|
|