|
F 2/1/13
|
HW due: Finish §8-6 #18,
which (cough, cough) few students had finished yesterday. Remember, you need
both a shells-based solution and a washers-based solution. Also write §8-6 #14,
15, and §8-7 #22. If you have time, please
do #14 and #15 with both a shells-based approach and a washers-based
approach. However, if time is short, you may omit one of the methods.
|
|
|
M 2/4/13
|
Special funutational
class. No additional HW is due today.
|
|
|
T 2/5/13
|
HW due:
1. Revisit the shells version of #15, which we did in class yesterday. Recall
that when the integral is set up as
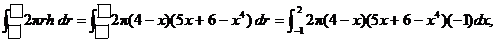
we obtain an answer that is off by a factor of –1. This occurs even though r = 4 – x clearly implies that dr = –dx. That is a true fact and is not the error. Where is the
error? We couldn’t find it yesterday, but that is only because we didn’t
spend enough time thinking clearly. Write a paragraph in which you elucidate
the situation and explain the mistake. Note:
Saying we made a sign error is not enough. Saying that we should use dx instead of
(–1)dx
is not enough. You need to find exactly where the mistake is and explain how
we could avoid it in the future. There is learning to be obtained here!
2. Write §8-5 #20abc.
|
|
|
W 2/6/13
|
HW due: Read §9-2; write
§8-7 #14, 16, §8-9 #11, 14, 15.
|
|
|
Th
2/7/13
|
HW due: Read §9-3; write
§9-2 #5 and #9 (using full work, explicitly showing u, du, v, and dv), §9-3 #3-21 mo3. For the §9-3
problems, you may use the “full work” technique of §9-2, the abbreviated work
of §9-3, or another method, as long as you show your work clearly.
Note: Work is required for all of
these problems, since you can produce the answers in an instant with wolframalpha.com.
It is strongly recommended that you use differentiation, not
wolframalpha.com, to check your answers.
|
|
|
F 2/8/13
|
HW due: Read §9-4; write
§9-3 #22-32 even, §9-4 #14, 16.
|
|
|
M 2/11/13
|
HW due:
1. Read §9-5.
2. Derive at least one of the reduction formulas in the green box on p. 449.
On your test, you will be given one of these and asked to derive it by using integration by parts. The
time-honored method of precal students (“Work both
ends to the middle and prove that they are equal”) is not acceptable for this
exercise. You must use integration by parts.
3. Memorize the identities in the green box on p. 452. These (and their
applications) may appear on a quiz and/or on the test.
4. Write §9-5 #2, 4. For each of these, use (a) a reduction formula and (b) a
helpful trig identity that allows the problem to be recast as a u-substitution.
5. Write §9-5 #8, 9, 12, 14, 29, 32.
|
|
|
T 2/12/13
|
HW due: Review problems,
minimum of 35 minutes’ worth. Log your time and bring written evidence of
what you worked on. Hashing through previously assigned problems is
permitted, but use a fresh sheet of paper with
Tuesday’s due date. Label the page number and problem number for each problem
that you work on.
In class: Review.
|
|
|
W 2/13/13
|
Test (100 pts.) on all material through §9-5. This will be a 40-minute test, since a Friday
schedule is in effect.
|
|
|
Th
2/14/13
|
HW due: Sleep.
|
|
|
F 2/15/13
|
No school (faculty
professional day).
|
|
|
M 2/18/13
|
No school (holiday).
|
|
|
T 2/19/13
|
HW due:
1. Read §9-6.
2. Read and work through as much of this
on-line tutorial on partial fraction decomposition as you can. The
on-line tutorial does a better job of teaching this subject than Mr. Hansen
does, so let’s take advantage of the technology!
3. Write §9-6 #1, 7, 17.
4. Use the “integral table” formula we proved in class last Thursday
(incorporating Sam D.’s timely chain-rule correction, of course!) to solve
§9-6 #15 in a jiffy. Or, you can do §9-6 #3 using one of the other formulas
we looked at.
|
|
|
W 2/20/13
|
HW due:
1. Read §9-8.
2. Complete (using trigonometric substitution) Tuesday’s in-class problem: 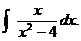
2. Write §9-7 #23abcd, 24abcdefgh.
|
|
|
Th
2/21/13
|
HW due:
1. Complete last night’s HW.
2. Read §9-9.
3. Write §9-8 #3, 6, 10. Show the integration by parts (sketchy work is
acceptable here).
|
|
|
F 2/22/13
|
HW due:
1. Complete the integration by parts in §9-8 #10 from last night’s HW.
2. Redo §9-8 #10 using washers (or shells, if you used washers the first
time).
3. Read §9-10.
4. Write §9-9 #3-21 mo3, 26, 27, 38a.
|
|
|
M 2/25/13
|
HW due:
1. Once again, if you have not completed §9-8 #10, do it! Be sure to check your work using the washer method (or
shells, if you used washers the first time).
2. Complete the other problems from Friday’s assignment.
3. Write §9-10 #3, 4, 9, 11, 12, 17, 19, 22.
|
|
|
T 2/26/13
|
HW due:
Write §9-11 #1-100 as follows. Don’t actually do the problems; simply make a
table as follows:

Use check marks in the table to indicate the method (or methods) that would
be appropriate for each problem. If one method is clearly preferable to all
the others in its row, circle the check mark.
The purpose of this exercise is to become proficient at recognizing the proper technique to use. Presumably you already
have some skill in applying the techniques, but it is also important to be
able to identify the right techniques.
Your table will have to run to at least 4 pages. You may abbreviate the
column headings on the continuation pages.
|
|
|
W 2/27/13
|
HW due:
1. Read §10-2. There is no new material here; it is all review. Remember that
reading notes are required, as always.
2. Write §10-2 #1, 2, 5, 6, 12, 13.
|
|
|
Th
2/28/13
|
HW due:
1. Read §10-3.
2. Write §10-3 #1-6 all, 13. The book’s solution to #13 is correct but not
very enlightening. Try to do your own proof for #13 without consulting the
back of the book.
|
|
