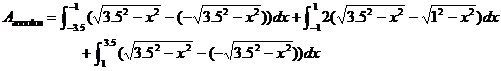|
W 1/2/13
|
Classes resume.
|
|
|
Th
1/3/13
|
HW due: Write §7-6 #13, 14,
15; read §8-2 and the green box on p. 368; write §8-2 #13, 14, 15.
|
|
|
F 1/4/13
|
HW due: Read §8-3; write
§8-3 #3, 2, 10, in that order.
|
|
|
M 1/7/13
|
HW due:
1. Read §8-4.
2. Read this handout that shows you exactly how to write up optimization
problems like those that were assigned: page
1 page 2 page 3.
3. Use the handout to correct and enhance §8-3 #3, 2, 10.
4. Write §8-3 #13, 19, 22. Work counts!
|
|
|
T 1/8/13
|
HW due:
1. Write §8-4 #6, 14.
2. Important: Use the remaining time
to clean up your previously assigned problems from §8-3. Make sure that your
solutions to #13, 19, and 22 are clean, and make sure that your solutions to
#2, 3, and 10 are positively immaculate. Copy the work from the handout into
your HW paper if you must. Solutions to #2 and #3 were provided previously,
and a complete solution to #10 is now
available as well.
|
|
|
W 1/9/13
|
HW due: Write §8-4 #16, 18;
then clean up all previously assigned problems from Chapter 8.
|
|
|
Th
1/10/13
|
HW due:
1. Show that the alternate approach (dy slicing) to §8-4 #6 gives the correct answer, 36, that
we obtained with dx
slicing.
2. Write §8-4 #15, 16, 17.
|
|
|
F 1/11/13
|
No additional HW is due, but
previously assigned problems from anytime in the second quarter may be
scanned. It is a safe bet that §8-3 #13, 19, and 22 will be among the
problems scanned.
|
|
|
Th
1/17/13
|
Midterm Exam (20% of semester grade), 8:00–10:00
a.m., SB-201/202.
Here are some additional resources to help you as you prepare for your exam:
·
Test #1,
9/26/2012 (blank copy)
·
Test #2,
11/29/2012 (blank copy)
·
Test #2,
11/29/2012 (solution key: page 1 page 2 page
3)
·
Test #3,
12/13/2012 (blank copy)
·
Test #3,
12/13/2012 (solution key: page 1 page 2 page
3)
Format of
the exam will be a mixture of
multiple-choice and free-response questions similar in difficulty and spirit
to AP-type questions. There is no point deduction for wrong guesses, other
than the points you fail to earn, which means that you should at least guess
at each problem. Do not leave anything blank. Scoring will be based on a
“curve” similar to the one used on the AP exam. Please bring spare batteries
to the exam.
|
|
|
W 1/23/13
|
Classes resume.
|
|
|
Th
1/24/13
|
HW due: Read §8-5; write
§8-5 #18, 26. It is strongly recommended that you do 1 or 2 odd-numbered
problems before attempting these.
|
|
|
F 1/25/13
|
HW due: Read §8-6; write
§8-5 #22. Make sure that your diagram is wlog. This
assignment should take you 10-15 minutes. Form V students, you are encouraged
to do the entire problem, but if you have no time because of the college
event, a neat wlog diagram showing the cone and the
equation of the slanted line segment that forms one edge of the cone will be
acceptable for full credit. Form IV and VI students are expected to do the
entire problem.
|
|
|
M 1/28/13
|
HW due: Read §8-7; write §8-7
#5, 8, 10, plus the problem below. Form V students must complete §8-5 #22 as
well. (Everyone else should have already done §8-5 #22.)
Problem: Prove that the volume of
any right pyramid equals 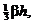 where where 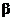 denotes the area of
the base. denotes the area of
the base.
|
|
|
T 1/29/13
|
HW due:
1. Read §8-9. This is a difficult section, so take your time and make good
notes. Also correct the typos in the textbook as follows:
p. 419 middle: write in the missing 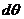
p. 420, green box: remove extra equal sign
2. Use the solution key (page 1 page
2 page 3) to grade your test, using
the following point system:
1a. work (3 points) + circled
answer (3) + units (2)
b. circled answer (3) + units (2)
2. work (4) + answer (4); many
alternate forms are possible in addition to those shown on the solution key
3. lenient grading: anything
believable (4) + believable derivative (2) + believable equation of line (2)
4. work (4) + correct value of a (4) + correct value of b (4)
5. proof (12) minus 4 for each
significant error, + Q.E.D./Halmos sign (1)
Note:
Failing to show why the limit
equals a product of an existing derivative value and zero is significant.
Several students had circular proofs, i.e.,
proofs in which continuity was implicitly assumed as a given.
Such proofs are generally scored as 2 points
out of 12, or 4 out of 12 if especially neat and clean otherwise.
6. use of 1/3 (3) + use of 0.05
(3) + use of weights 1,4,2,4,... (4) + plugged-in values of force (4) + units
(2)
7. explanation (5) that number of
intervals must be even and/or that number of mesh points must be odd
Note:
Half credit for failing to say what n
is or for getting the rule backwards; no credit if multiple mistakes.
8. answer (5); work is not
required, but deduct 5 for use of L’Hôpital’s rule,
even if answer is correct
9. considering ln
(3) + saying 0/0 L’Hôp. (2) + using L’Hôp. (5) + getting lim of ln of answer as –4 (5) + e–4 (5)
Note:
Final 5 points can be earned by giving answer (circled) as e to whatever power you had, even if
wrong.
Please use a different color of ink (blue or green recommended), and mark your
estimated score at the top of the first page. Your score will probably not
precisely match the score that was recorded for you in Q2, but you should be
able to come close.
|
|
|
W 1/30/13
|
HW due: Solve the problem
below. For each subpart, (a) through
(f), furnish a sketch and clear, convincing work. Be sure to sketch the
entire figure as well as a “wlog” element chosen
from within it.
1. Consider a “hockey puck with a hole in it.” The object is a little bit
like a torus (“bagel” or “doughnut”), except that the cross sections parallel
to the axis of rotation are rectangles, not circles. The diameter of the
“hockey puck with a hole in it” is 7 cm, and the diameter of the hole is 2
cm. The height of the object is 2.8 cm. If you can’t visualize the object,
think of an angel food ring cake like the one we ate yesterday, only much
smaller.
(a) Compute the total surface area, using any method you find appropriate.
Explain your reasoning clearly. (No credit for random bits of expressions
that are added together without clear indication of where they came from.)
(b) Compute the volume in the most straightforward possible way, as the
difference of two right circular cylinders.
(c) Compute the volume by plane slicing (planes perpendicular to the axis of rotation).
(d) Compute the volume by plane slicing (planes parallel to the axis of
rotation). This one is hard, and you can save it for the end if you wish.
(e) Compute the volume by radial slicing.
(f) Compute the volume by cylindrical shells.
|
|
|
Th
1/31/13
|
HW due: Write §8-6 #2, 4
(using both shells and washers), 13 (using both shells and washers), 18
(using both shells and washers). Note:
Even though you are to explain in #18 why cylindrical shells are not
appropriate, the better term to use would be “not optimal.” You can and
should use cylindrical shells to cross-check the answer you obtained with
washers.
Yesterday’s assignment will also be collected a second time. If you did not
already provide a sketch for each of the subparts, you should do that now.
Patching up yesterday’s assignment does not count toward your 35-minute time
log. You may use the work below to assist you in solving part (d).
Area of the annulus by slicing perpendicular to the x-axis (i.e., parallel to the imaginary z-axis that comes vertically out from the origin):
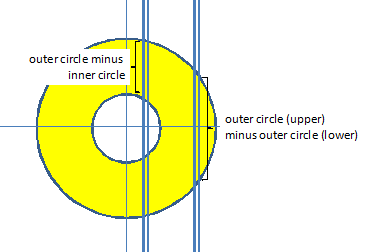
Note: Equation of outer circle is 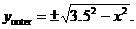 Equation of inner circle is Equation of inner circle is 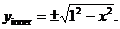
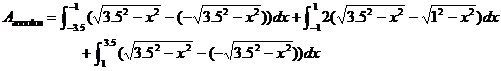
By quadrature, this area is approximately 35.342918
sq. units. Multiply by 2.8 to get 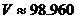 cu. units. cu. units.
You can also set up your integrals having integrands containing a factor of
2.8 (for the z height), which means
that instead of computing the area of the annulus, you compute the volume
directly. If you take that approach, you should think of the cross sections,
which have width given by a difference of radicals and height given by the z height value, namely 2.8.
Note: The height that is “thrown
into” the integrand must either be a constant or a function of the
independent variable, which is x in
this problem. If the height is not a function of x, you will need techniques more advanced than the techniques of HappyCal to compute the volume.
|
|