|
W 9/5/012
|
First day of class.
|
|
|
Th
9/6/012
|
HW due:
1. Read §1-1.
2. Send Mr. Hansen an e-mail message. Remember to put a double underscore ( __ ) at the start of your subject line.
|
|
|
F 9/7/012
|
HW due:
1. Numerous people must have sent messages without a double underscore ( __ )
in the subject line, because I did not receive 21. Please check your “Sent
Mail” folder, and re-send if necessary with the proper subject line.
2. Watch the video entitled “Greek Letters for the Calculus” and the video
entitled “Roman Letters for Variables.” Both videos are available by clicking
the “VIDEOS!” link at the top of Mr. Hansen’s
home page. Total running time is about half an hour. Be prepared for a
quiz.
|
|
|
M 9/10/012
|
HW due:
1. Using the same video link you used last week, watch the video on Hippasus. This video is pitched for students at a lower
level than HappyCal, but don’t skip through it.
Actually work through the proofs, and make sure you understand each step
along the way. Note-taking is encouraged.
2. A continuous function f is
defined, in part, by the following table of values:
|
|
|
|
|
|
|
|
|
x
|
f (x)
|
|
|
|
|
|
|
|
|
0
|
3
|
|
|
|
|
|
|
|
|
1
|
4
|
|
|
|
|
|
|
|
|
2
|
7
|
|
|
|
|
|
|
|
|
3.5
|
15
|
|
|
|
|
|
|
|
|
4.5
|
23
|
|
|
|
|
|
|
|
Estimate the derivative when x = 2.
In other words, we are asking for an estimate for the value of 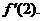
Use
(a) a graphical approach,
(b) a numerical approach (i.e., based on the table),
(c) an analytic approach (based on finding a suitable curve that fits the
data well), and
(d) a verbal approach (justify a believable value for the slope of the curve
at x = 2, based on some discussion
of the function’s behavior before and after 2).
Note several things:
·
There is no
guarantee that f is differentiable.
Thus it is possible that 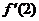 might not exist at
all. However, let us try to find reasonable estimates for what might not exist at
all. However, let us try to find reasonable estimates for what 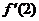 might be if the
function is differentiable at x = 2
and monotonic on [0, 4]. might be if the
function is differentiable at x = 2
and monotonic on [0, 4].
·
We’re asking
for estimates, not a precise value.
·
The different
methods may yield different estimates. That is OK.
·
Graph paper is
not required in part (a). Any reasonably neat sketch with relatively uniform
tick-mark spacing should give you enough accuracy to make a respectable
estimate.
3. Last week, nobody (!) was lured into the classic
student error of saying that if f (x) = ex, then 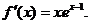 My explanation is
that you were taught extremely well by Mrs. Dunn. Explain why the proposed
(wrong) answer of xex
– 1 could not possibly be correct, without making use of the fact that
the true derivative function is ex,
not xex
– 1. Write a paragraph (with
correct spelling, punctuation, and grammar) to explain why the xex
– 1 function does not have the right characteristics that a true
derivative function would need to have. A sketch to accompany your paragraph
is optional. My explanation is
that you were taught extremely well by Mrs. Dunn. Explain why the proposed
(wrong) answer of xex
– 1 could not possibly be correct, without making use of the fact that
the true derivative function is ex,
not xex
– 1. Write a paragraph (with
correct spelling, punctuation, and grammar) to explain why the xex
– 1 function does not have the right characteristics that a true
derivative function would need to have. A sketch to accompany your paragraph
is optional.
Note: For #3, do not resort to a
formal argument. Yes, the calculus is a formal system, and we frequently
resort to formal arguments (i.e., arguments based on formalisms, without
regard to the underlying meaning). That’s not what you are supposed to do
this time. You’re going to have to think hard and write a thoughtful
paragraph. Arrgghh!
WRONG ANSWER (no credit): Our
textbook says that if f (x) = ex, then the derivative is ex. That is not the same function as xex
– 1. Therefore, xex
– 1 cannot possibly be correct. (Q.E.D.)
WRONG ANSWER (partial credit): The
function xex
– 1 is always negative. [This student is wrong, but at least he is
trying to think in a non-“cookbook” fashion.]
|
|
T 9/11/012
|
HW due: Read §1-2 and prove (using a truth table)
that 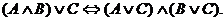
|
|
W 9/12/012
|
HW due: Read §1-3; write §1-2 #26, 27; write §1-3
#10, 12.
|
|
Th
9/13/012
|
HW due: Read §§1-4 and 1-5; write §1-4 #4 (using the
trapezoid rule), #12 (use formula 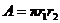 for the final part),
and the additional question below. for the final part),
and the additional question below.
A1. Negate the limit definition. In other words, write exactly what it means to say that the real number L is not the limit of a function f (x)
as x approaches c. Be sure to carry the negation (~
symbol) all the way “inside.”
|
|
F 9/14/012
|
HW due: Read §§2-2 and 2-3; write §2-2 #11, 13, and
the additional question below.
A2. Correct #A1 from yesterday’s assignment. Then use that result to prove,
rigorously, that 4.1 is not the
limit of the function y = f (x)
= 3x as x approaches 1.4.
Note: It is not acceptable in this
exercise to state that the correct limit is 4.2, and since 4.1 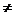 4.2, the limit
cannot be 4.1. Instead, show that there exists a positive 4.2, the limit
cannot be 4.1. Instead, show that there exists a positive 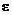 such that for any positive such that for any positive 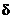 , a punctured , a punctured 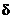 -neighborhood of 1.4 will . . . [finish the thought]. -neighborhood of 1.4 will . . . [finish the thought].
|
|
M 9/17/012
|
HW due: Read §§2-4 and 2-5; write §2-3 #22 (use MATH
8 to check your answer), §2-4 #67c (use a
= 2, and provide a rigorous proof of continuity), §2-5 #12, and the
additional problem below.
A3. Here are some of the negated limit definition attempts submitted by Form
VI students. Each of these contains one or more errors. Read through these
and prepare to describe, orally, what the student’s misconception seems to
have been in each case. Note: It
does not suffice to say, “Do it this way.” You have to imagine what it was
that the student was thinking, and then try to guide him to a better
understanding. Oral preparation is acceptable for these problems; written
notes are suggested but are not required.
Student 1:
There exists an epsilon greater than zero for all delta greater than zero such that |x – c| is between 0 and
delta, exclusive, and |f (x) – L| is greater than or equal to epsilon.
Student 2:
There exists an epsilon greater than zero for all deltas
greater than zero such that |x – c| is either less than zero or greater
than delta OR |f (x)| is less than epsilon.
Student 3:
There exists a positive epsilon for any positive delta such
that (0 < |x – c| < delta) 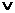 ~ (|f (x)
– L| < epsilon). ~ (|f (x)
– L| < epsilon).
Student 4:
There exists a positive epsilon for any positive delta such
that [0 < |x – c| < delta] and |f (x)
– L| is greater than or equal to
epsilon. [Side question: Do you think students 3 and 4 worked together?]
Student 5:
For any delta greater than zero, there exists an epsilon
greater than zero such that zero is less than |x – c|, which is less
than delta, and the absolute value of f
(x) minus the limit as x approaches c is greater than epsilon.
Student 6:
There exists an epsilon greater than 0 for any delta
greater than 0, such that there exists an x
with 0 < |x – c| < delta and |f (x)
– L| is greater than or equal to
epsilon.
Warning: In class, you will also be
asked which of these 6 comes closest to the true answer, and you may be
required to defend your choice.
Optional additional question to ponder:
This is a crucial question, though it seems not to have crossed the minds of
many students. The question is, “What is x?”
|
|
T 9/18/012
|
HW due: Now that you know exactly how to write a properly negated limit definition (you do,
don’t you?), revisit the previously assigned problems and make sure they are
done properly. If you wish to begin anew with a fresh sheet of paper, that is
fine. If there were any problems that you could not reach previously because
of time limitations, this is your chance to get caught up.
If you would like to send your negated definition for reassurance, just to
make sure that your version is correct, that is fine. E-mail will be accepted
until about 10:45 p.m. Monday.
|
|
W 9/19/012
|
HW due: Read §2-6; write §2-6 #9, 10, 12, 13, 14.
|
|
Th
9/20/012
|
HW due: Read §§3-2 and 3-3, plus the green box on p.
89; write §3-2 #8, 15, 16.
|
|
F 9/21/012
|
HW due:
1. Read §3-4.
2. Sketch a function f that has
some “unusual” features: discontinuities, an asymptote or two, one or more
straight segments, a few cusps, at least one sinusoidal region, and at least
one exponential region. On a separate set of axes aligned directly
underneath, make a careful sketch
of 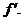 Remember that sinuosoids have sinusoidal derivatives, and exponentials
have exponential derivatives. Remember that sinuosoids have sinusoidal derivatives, and exponentials
have exponential derivatives.
3. Ask one or two trusted friends to proofread your question and answer in
#1. If you have an insufficient number of friends or cannot locate them in
time, bring your paper to class at about 7:55 a.m. to have Mr. Hansen look at
it.
4. Why is it improper, strictly speaking, to graph a function and its
derivative on the same set of axes?
5. Prove that the derivative of any second-degree polynomial is linear. For
full credit, your proof must end with “Q.E.D.” or the Halmos
sign.
6. Prepare §3-4 #1-14 all for oral presentation. (Written work is permitted
for these but not required.)
7. Write §3-4 #30.
|
|
M 9/24/012
|
HW due: Start working
on the following review problems. All you have to show for today is evidence
that you made a solid start. These problems are due in full on Tuesday.
1. Define symbols clearly (for example, write “Let P = event that Peter says ‘please’”) and then encode the following
sentence using suitable symbols only, no words:
If Peter says ‘please,’ then all of the fish in the tank will blow bubbles.
2. Write the converse, the inverse, and the contrapositive
of the sentence in #1.
3. Explain why “Some of the fish in the tank will blow bubbles” is neither
equivalent to the conclusion of #1 nor equivalent to the negation of the
conclusion of #1. Use symbols and quantifiers where appropriate.
4.(a) The word calculus
originally meant, in Latin, “pebble.” Pebbles can be used as placeholders to
perform certain types of calculation without thinking, for the moment, about
the underlying meaning of what one is doing by manipulating pebbles. What do
we mean nowadays when we say “a calculus”?
(b) Is it meaningful to speak of “a calculus of bond
pricing”? Why or why not? Write a sentence or two, nothing more.
(c) What do we mean by the word formal? [Hint: For this
and all other words used in class, you should be sure you understand exactly
what they mean.]
5.(a) Simplify the following messy expression to the
greatest degree possible. Then use a truth table to prove that your answer is
equivalent to what you started with.
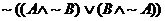
(b) Is the expression in (a) a tautology? Why or why
not?
(c) If the expression in (a) is true, can we conclude
that atom B is false? Why or why not?
(d) If the expression in (a) is true and atom A is
true, can we conclude that atom B is false? Why or why not?
6. Explain in approximately 2 to 3 sentences why we never permit wording such
as the following: “All of the lawyers in that firm are not respectful of
smokers.”
7. Who developed the calculus?
8. Negate the following: “For every problem in Myrna’s textbook, there exists
a solution to that problem such that the solution is both contained within
pages 1408-1531 and is correct.” Carry the “~” symbol as far as you can.
9. Prove, rigorously, that 18 is the limit of the function y = f (x) as x approaches 4.5, where y is defined to equal 4x if x > 4.5, and y = 18
otherwise. Use the customary epsilon-delta notation.
10.(a) In #9, what feature does f (x) have at x = 4.5?
(b) Sketch the graph of dy/dx in #9.
(c) Give two additional names (notations) for dy/dx in #9.
(d) If we had used q = v(t) instead of y as a function of x,
give three notations for the derivative.
(e) Use the rule of GNAV to give four different
interpretations for dy/dx in #9, at
the point where x = 4.5, and
explain in each case why failure occurs.
(f) Does dy/dx,
considered as a function in #9, have a limit from the left as x approaches 4.5? If yes, give
notation and answer, not merely a “bare answer.” If not, explain why not.
(g) Explain why dy/dx in #9 does
not have a two-sided limit as x
approaches 4.5. Use correct notation and the smallest number of words you can
get away with.
(h) Explain why dy/dx does not exist at x = 4.5.
(i) Can you use (f) and (g)
as lemmas to prove (h)? Why or why not?
11. Do the Chapter Test on pp. 35-36, except that for T5,
do part (e) only.
12. Do the Chapter Test on pp. 74-76, but only the following problems: T6,
T8, T9, T10, T11, T12.
13. On p. 126, write #T3 and #T5 only.
|
|
T 9/25/012
|
HW due:
Finish your review problems.
In class: review.
|
|
W 9/26/012
|
Test (100
pts.) on everything covered so far.
After you have finished your studying, you may wish to try these
sample questions. An answer
key is also available. Warning:
Do not look at the questions until after you have finished your studying.
These are not review questions, and they are not comprehensive. If you use
them to guide your study, you will miss a great deal of content.
Another warning: Do not look at the
answer key until after you have given your best effort to all the questions.
Otherwise, you’re merely deluding yourself. Anyone can say, “Yeah, yeah,”
after looking at the answer. It takes a brave person to put himself on the
line with an answer toward which he has given his best effort. DON’T GUESS UNLESS YOU ARE WILLING TO
GUESS RANDOMLY.
|
|
Th
9/27/012
|
No additional HW due. A rare night off! Get some
sleep . . . you are very sleepy . . .
|
|
F 9/28/012
|
HW due: Read §§3-5 and 3-6; write §3-5 #2, 8abcd,
§3-6 #3, 4. Prepare §3-6 #7 for oral presentation only.
Hint: In #3, store g(x)
into function Y1 as directed. Put your conjectured derivative
function into Y2 as directed. Then, enter nDeriv(Y1,X,X)
into function Y3. You can usually find nDeriv
under MATH 8, but if not, use 2nd CATALOG to find it.
|