|
W 2/1/012
|
Test (100
pts.) on all material covered since the midterm.
|
|
|
Th
2/2/012
|
HW due: Read pp. 475-480, 482-492. Part of your assignment
is to circle or highlight the italicized passage in the middle of p. 487. Note: The confidence level (e.g., 95%)
is not a probability associated
with any particular interval. Rather, it is the relative frequency with which
the method will, in the future,
generate an interval that brackets the true value of the parameter.
Therefore, any probability statement made with regard to confidence intervals
is dangerous. The “approved safe wording” for the AP exam is to say something
like this:
We are 95% confident that the true mean is between 38.09
and 43.17.
Do not say this:
There is a 95% probability that the true mean is between
38.09 and 43.17.
|
|
|
F 2/3/012
|
HW due: Write #9.2, 9.5, 9.6, 9.8.
For #9.5, 9.6, and 9.8, also check the
assumptions and write a 95%
confidence interval, in context, for the parameter of interest. You may
use “button-pushing” (STAT TESTS 8, STAT TESTS A) to obtain the intervals,
and you do not need to show work. However, your conclusion must be in
context. See #9.3, which is done for you below as an example.
9.3. Given: 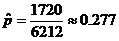
Check: SRS? Not stated. Assume “random” here means SRS. 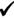
Is N 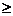 10n? Yes, since n is many millions, and 10n
= 10(6212) = 62,120. 10n? Yes, since n is many millions, and 10n
= 10(6212) = 62,120. 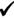
Is np 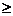 10? Yes, since np 10? Yes, since np 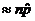 = 1720 >> 10. = 1720 >> 10. 
Is nq 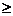 10? Yes, since nq 10? Yes, since nq 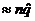 = 6212 – 1720 = 4492
>> 10 = 6212 – 1720 = 4492
>> 10 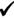
By calc., 95% C.I. is (0.266, 0.288).
Conclusion: We are 95% confident
that the true proportion of U.S. children that eat fast food on a typical day
is 0.277 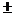 0.011. 0.011.
|
|
|
M 2/6/012
|
No class.
|
|
|
T 2/7/012
|
No additional written HW due. Use this as an opportunity
to get caught up on previously assigned problems, all of which should now be
complete.
|
|
|
W 2/8/012
|
HW due:
1. Read pp. 495-496.
2. Forget every word on pp. 495-496.
3. Then read from bottom of p. 496 (“Confidence Interval for 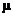 when when 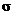 is Unknown”) through
p. 505. is Unknown”) through
p. 505.
4. Write #9.16. Note: Checking
assumptions and writing a conclusion in context are required. See 2/3
calendar entry for the format to use.
5. If you did not score a 4 (out of 4) on the homework due last Friday, 2/3,
then redo those problems until they are all excellent. They may be collected.
|
|
|
Th
2/9/012
|
HW due:
1. Watch the remainder of the Ken
Robinson video.
2. Prepare for a quiz on all recent material: confidence intervals (both z and t), checking assumptions, and writing conclusions in context.
Remember, we use z intervals (STAT
TESTS A) for proportions and t
intervals (STAT TESTS 8) for means. We do not use STAT TESTS 7 at all.
|
|
|
F 2/10/012
|
HW due: Write #9.30abcdefg, 9.31abcdef, 9.32, 9.34, 9.47.
A quiz on older material is also possible. (See topic list in yesterday’s
calendar entry.) A cheat sheet for the assumptions is available here. For now, look only at the
lines for STAT TESTS 8 (t interval
for mean) and STAT TESTS A (1-prop. z
interval).
|
|
|
M 2/13/012
|
HW due: Read pp. 508-513 and the summary on p. 517;
write #9.38, 9.68.
Note: Checking assumptions is required
for both problems. You are explicitly asked to do this in #9.38c, but you
also need to check assumptions for #9.68 in order to earn full credit.
|
|
|
T 2/14/012
|
HW due: Review questions #9.52, 9.57, and any other
3 of your choice on pp. 518-521. Odd-numbered problems may be more to your
liking, since the answers are in the book, but you may choose whichever ones
you wish after you have done #9.52 and 9.57.
Suggestion: Be sure to practice checking
your assumptions. It is a good idea to practice both “worlds”: the world of
proportions (z intervals, STAT
TESTS A) and the world of means (t
intervals, STAT TESTS 8). Both worlds will be on the test. A t* table similar to the one on the
inside of the back cover of your textbook will be provided. Note that the
line for “infinitely many degrees of freedom” corresponds to z*, since the z distribution can be considered to be the limit of the t distributions as 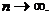
|
|
|
W 2/15/012
|
Test (100
pts.) on all recent material.
|
|
|
Th
2/16/012
|
HW due: Answer all questions on the family vacation exercise from
yesterday’s test. You may write directly on the handout. Please arrive a
bit early to class, if possible, in order to 3-hole punch your paper.
Note: The symbols may be a little
hard to read in part (e) of the problem. The problem is requesting sigma (i.e., the true population s.d., which requires that you remember all the way back
to last fall when we were working with random variables) and sigma sub xbar,
the s.d. of the sampling distribution of means when
n = 40.
|
|
|
F 2/17/012
|
No school.
|
|
|
M 2/2/012
|
No school.
|
|
|
T 2/21/012
|
HW due: Read pp. 525-558. Reading notes are
required, as always. Read all examples, but you may omit the exercises for
now. This is a total of 28 pages of actual reading. An open-notes quiz is
possible.
|
|
|
W 2/22/012
|
HW due: Watch the rest of the 60 Minutes video, from 8:42 to the
end (i.e., the final 5 minutes). Pay special attention to what the FDA
official, Dr. Thomas
Laughren, has to say about “basic statistics”
(9:43 to 10:03). Write answers to the following questions.
1. The abbreviation ES (for “effect size”) is frequently used in statistical
writing. Paraphrase Dr.
Kirsch’s findings using the abbreviation ES at some point in your
writing.
2. Instead of viewing only Dr. Laughren’s response
(9:43 to 10:03) to Leslie Stahl’s question, view the entire exchange in
context, starting at about 9:18. Critically analyze Dr. Laughren’s
response to the question regarding the two positives and whether they are
“deserving of bigger strength in the decision.” Remember that Dr. Laughren holds an M.D. degree and has surely taken not only
basic statistics but probably more advanced courses in biostatistics as well.
Does he properly interpret the meaning of P-value
for a lay audience, or does he fumble the question? You may find this Wikipedia article
to be helpful as you formulate your response. Also keep in mind that editing
of video can play subtle tricks. Thus we cannot hold Dr. Laughren
to an unreasonably high standard. If he essentially
states what “basic statistics” has to say about the probability of chance
occurrences, we have to give him credit.
For #1, a sentence or two will suffice. For #2, a thoughtful paragraph is
expected. Responses for both questions must be in your own words.
Also today, we will have our “pure extra credit” quiz rehashing some of the
same material from the most recent test. Make sure that you know how to
calculate the s.d. of a random variable by using
the STAT CALC 1 L1,L2 ENTER
trick.
|
|
|
Th
2/23/012
|
HW due: Write #10.47 (make a quick sketch for each
of the 7 parts), 10.49 (make a single sketch for all 3 parts).
|
|
|
F 2/24/012
|
HW due (web server down): Write #10.47 (make a quick
sketch for each of the 7 parts), 10.49 (make a single sketch for all 3
parts). Note: This is a rehash of the previous assignment. Make sure
it is done well, with all answers complete! And then, get some good sleep.
|
|
|
M 2/27/012
|
HW due Monday: Fill in the blanks on this mini-project (Word file in .DOC
format). If you do not have Word, or if your printout has obvious errors
in the Greek letters or mathematical notation, then use the .PDF version instead.
|
|
|
T 2/28/012
|
HW due: We are going to do another mini-study. This
one uses a 2-proportion z test
(STAT TESTS 6) instead of a 2-sample t
test. The research question is this: “When a fair coin is flipped 5 times, is
the probability of obtaining a head that is immediately preceded or followed
by 2 tails in a row different from the probability of obtaining exactly 2 or
3 heads (in any order)?”
Note: It is not immediately obvious
which probability is greater, or even whether the 2 probabilities differ. You
can compute them if you wish, but that is not the point of this exercise.
1. Define your parameters. Hint:
For this problem, the parameters are p1
and p2.
2. Write null and alternative hypotheses. A 2-tailed alternative is
recommended, but if you feel bold, you can try your luck with a 1-tailed
alternative.
3. Gather data from at least 30 series of 5 flips. That means that your
sample sizes, n1 and n2, are both 30. If you
find flipping a real coin to be excruciatingly boring, you may use a random
number generator instead: randInt(0,1) where 0=tail, 1=head. For event 1, you are looking
for patterns like 00010 or 00100 or 11001, all of which would be successes.
For event 2, successes would look like 10101 or 11000 or 01110.
4. Record all your raw data. Note:
For recording purposes, 0 and 1 are much faster to write than “H” and “T”
(and easier to tabulate, too).
5. Compute 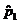 and and
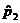 , the sample proportions of success. Write them down using
proper notation! , the sample proportions of success. Write them down using
proper notation!
6. Punch the buttons to perform a 2-proportion z test. Write your P-value
and a conclusion in context.
|
|
|
W 2/29/012
|
HW due:
1. Read the PHA(S)TPC handout.
Note that we have practiced all of these steps recently except for A, which
is the hardest.
2. Read the rows that are numbered 2, 4, 5, and 6 on the STAT TESTS handout. Start
memorizing those rows, a little bit each day. You have to know all the
assumptions cold.
3. Using neat block lettering, print the following letters exactly as shown
(or print this paragraph, and cut and mount the letters on a piece of paper):
JFKC IAF BIU SASA TGP AGR EIB MN BAC PR
4. On a second sheet of paper, hand-print or print the following letters in
the same size as before:
JFK CIA FBI USA SAT GPA GRE IBM NBA CPR
5. Recruit 4 or more test subjects. You can deal with them one at a time or
in small groups. Ask each subject to memorize as many nonsense words from the
first sheet as they can in 20 seconds. (Time them carefully.) Then, ask them
to write down as many of the nonsense words from memory as they can in 90
seconds. (Most people will not use the full 90 seconds.) After they have done
that, show them the second sheet. Tell them that it contains the same exact
letters as before, grouped in a different way. Give them 20 seconds as
before, followed by 90 seconds to write down as many words as they can
remember.
6. Scoring: For each test subject, record how many words were fully correct
from each trial (trial 1 and trial 2). There is no partial credit. For
example, if a subject writes “BUI” for trial 1, there is no credit.
Use a table similar to this to record your data:
7. Because the second trial was so much easier, plus the subjects had the
benefit of a learning effect, we would expect the mean score for trial 2 to
be greater than the mean score for trial 1. However, since the subject scores
are “paired” in a natural way, with each subject serving as his own control,
we call this a matched pairs study.
It is not a 2-sample t test; it is a 1-sample t test on the differences. Mark the
rightmost column “Difference (trial 1 – trial 2)” and compute the
differences. Note: These
differences will probably be negative numbers.
8. Define the parameter (singular) of interest.
9. Write null and alternative hypotheses.
10. Check assumptions: SRS, normal pop. of
differences, unknown s.d.
11. If you wish, sketch the sampling distribution of differences, assuming
that H0 is true.
12. Compute the t statistic and the
P-value of the test. You can do
this by punching buttons on your calculator.
13. Write a conclusion in context.
|
|
