|
T 1/3/012
|
Classes resume.
In class: Review.
|
|
|
W 1/4/012
|
Review Quiz #1: Focus on notation, terminology,
exploratory data analysis, and linear least-squares regression.
|
|
|
Th 1/5/012
|
Review Quiz #2: Focus on curve fitting, probability,
and positive predictive value (PPV). For a good example of a PPV problem,
look at #17-20 from the 12/12/2005 test.
(Note: You are not yet expected to
know the terms “null hypothesis,” “Type I error,” and “Type II error,” but
you are expected to know “false positive,” “false negative,” and how to
compute PPV.) Be sure to work the problems before you check the solution key.
|
|
|
F 1/6/012
|
Review Quiz #3: Focus on curve fitting and residual
plots.
|
|
|
Exam Prep
|
The following resources are provided to help you
prepare for Monday’s midterm exam:
·
College Board
website
AP
Stat home page: course description, 2 full-length sample exams, study
guides, and more
Sample
exam questions
·
Test
(11/15/2011) on Probability and Transformations (class mean = 70%)
Blank copy of in-class portion
Blank copy of take-home
portion
Solution key for in-class portion
Solution key for take-home
portion
·
Big Quiz
(12/21/2011) on Random Variables (class mean = 55.7/60, or 93%)
Blank copy
Solution key
·
Please send
e-mail to Mr. Hansen over the weekend (double underscore in subject line,
please) if you have any questions.
|
|
|
M 1/9/012
|
Midterm
Exam, 8:00 a.m., MH-315. If MH-315
proves to be too small, we may move to another nearby room, but we will start
in MH-315.
Format will be a reduced-scale AP exam, as follows:
Part I. Multiple Choice. There
will be 22 questions in 50 minutes. Work is not graded in this part of the
exam. There is no penalty for wrong guesses, since the penalty was phased out
in 2011.
Part II. Free Response. There will
be one multi-part question of standard length (13 minutes) and one
“project-type” question that requires in-depth thinking and writing (25
minutes).
Examples of all these types of questions can be found on the College Board
website (see link at bottom of STAtistics Zone webpage) or in your Barron’s
review book. You are responsible for all information covered in the textbook
through Chapter 7, except for a few passages that we skipped here and there,
such as §7.8. If you have any doubt about the reading assignments, please
check the “archives” link at the top of the schedule.
We should be finished with the exam by about 9:30 a.m. In my experience, most
students have ample time during Part I and run out of time in Part II.
However, there is no extended time. All scores will be based on a modified
“AP curve” in which an A (AP score of 5) generally requires a score in the
mid-70s. As always, Mr. Hansen will use judgment to ensure that the curved
scores make sense in context.
What to Bring to the Exam
Pencil is REQUIRED
for Part I. You may use either pencil or pen for Part II.
A graphing calculator is required throughout. Bring
spare batteries, since if your calculator dies partway through, you will be
out of luck.
Scratch paper is not allowed.
A standard AP formula sheet will be provided for
you. Examples are available both in your Barron’s book and in the Course
Description PDF file (available on the College Board website).
One question you often see on the AP exam is one
that asks you to “interpret the slope of the linear regression in the context
of the problem.” For example, you may have a LSRL that uses speed (mph) as
the explanatory variable and fuel economy (mpg) as the response variable, and
maybe the slope is –0.28. Here is the wording you would be expected to
provide for full credit:
For each additional mile per hour of
speed, the linear model predicts a fuel economy reduction of 0.28 miles per
gallon.
Note that all of the following are incorrect:
“Miles per gallon are predicted to be –0.28 times the speed in mph.” (No,
that’s not what the LSRL says.)
“Each additional unit of x is
associated with a reduction of 0.28 in y.”
(Not in context of problem. Fail!)
“Miles per gallon decreases by 0.28 for each additional mile per hour.” (No,
that’s only what the model predicts.)
“Speed is predicted to decrease by 0.28 mph for each additional mile per
gallon.” (No, that’s backwards.)
“Miles per gallon are predicted to change by 0.28 for each additional mph in
speed.” (Vague, sign omitted.)
|
|
|
W 1/18/012
|
Classes resume.
In class: Discussion of midterm exam.
Evening: Attend The Prep School Negro
at Trapier Theater.
|
|
|
Th 1/19/012
|
No additional HW due. This is in order to provide
time for you to attend Wednesday night’s screening.
|
|
|
F 1/20/012
|
HW due: Fill out your “I/E/P” (Incorrect/Partially
Correct/Essentially Correct) ratings, using the scoring rubrics found here
(Question 1) and here
(Question 6). If you wish to see the original text of the questions,
check here
and here.
|
|
|
M 1/23/012
|
HW due: Read pp. 445-449 twice. This is not super-exciting reading, but it concerns the
most important abstract concept of the year, the concept of a sampling
distribution. There may be an open-notes quiz today to check for reading
comprehension.
|
|
|
T 1/24/012
|
HW due: Read the following paragraph and take some reading
notes. Then read pp. 451-459 and do the exercise at the bottom.
Reading Assignment to Supplement pp.
451-459:
AP Statistics is concerned with 4 principal topic areas, namely
– exploratory
data analysis
– design of
experiments and surveys
– probability
(including simulations and random variables)
– inferential
statistics
We did the first 3 in the first semester. The last topic will take us the
rest of the year. Inferential statistics deals with many questions, but the
most important goal is this: We use
statistics in order to estimate parameters.
The two most important abstract concepts in the second half of the course are
sampling distributions and statistical significance. You need to
write your own definition, in your own words, of “sampling distribution,” but
basically it should be something like this: the set of all possible values
that a statistic can have when samples of a fixed size are chosen from some
population of interest. As for statistical significance, that is a
determination that a difference is too large to be plausibly explained by
chance alone, or to put it another way, that a statistic is too far out in the tail of the purported
sampling distribution to be plausibly explained by chance alone.
Statistical significance means that, as far as we can tell, the observed
difference in means (t
distribution) or proportions (z
distribution for 1 or 2, 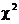 distribution for 3
or more) is most likely not a
fluke. If we have statistical significance, we are saying that the observed
difference is meaningful in some sense. distribution for 3
or more) is most likely not a
fluke. If we have statistical significance, we are saying that the observed
difference is meaningful in some sense.
Warning: Statistical significance
cannot be found hiding in a pool of data. We are not on a “witch hunt” for
statistical significance, poking around patiently until we find some
statistical significance somewhere. If we did that, we would be committing
the “Texas sharpshooter fallacy,” a.k.a. the “data mining fallacy.” The
reason is that any sufficiently large set of data will contain, by chance
alone, some interesting patterns. We have to assert in advance that a pattern exists, then gather data to prove that
the pattern exists to a degree that could
not plausibly be explained by chance alone.
If you are familiar with Babe Ruth and the legend of the “called shot,” you
understand exactly what the distinction is. If Babe Ruth had said, at the
beginning of the season, “I will hit some home runs,” there would be no
story. Boring! No significance! Since he was a power hitter (also a power
striker-outer, but that is another story), it was a safe bet that he would
hit some home runs. However, for him to point to a certain place in the
outfield, as he did (according to the legend), and then hit a home run to
that precise location, moments later, was certainly impressive.
In the same way, we would have some persuasive proof if we assert that a
certain pattern exists, then gather data to show that the pattern exists to a
degree that cannot be plausibly explained
by chance alone. However, finding a few statistics that are
“statistically significant” in a large data set is not surprising at all.
Exercise:
The green box at the top of p. 457 says that the CLT can be safely applied if
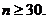 However, some
distributions have such extreme skewness and/or “fat tails” that even n = 40 or 50 would not suffice for
approximate normality of However, some
distributions have such extreme skewness and/or “fat tails” that even n = 40 or 50 would not suffice for
approximate normality of 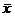 . At the end of the following paragraph, your textbook
says, “In practice, however, few population distributions are likely to be
this badly behaved.” Comment briefly, taking the crash of 2008 into account. . At the end of the following paragraph, your textbook
says, “In practice, however, few population distributions are likely to be
this badly behaved.” Comment briefly, taking the crash of 2008 into account.
|
|
|
W 1/25/012
|
Quiz on recent class discussions. It is a safe bet, for
example, that you will have to state the CLT.
HW due: Mark notational changes to the tan box on p. 465 as described below;
read pp. 461-466; write #8.20.
Note: When reading pp. 461-466,
remember that the notation used by our textbook (and many other college-level
textbooks) is to let p = sample
proportion (statistic), 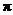 = population
proportion = probability (parameter). This is consistent with the general
rule that Roman letters are used for statistics, while Greek letters are used
for parameters. However, the AP exam uses a different notational convention,
which is that = population
proportion = probability (parameter). This is consistent with the general
rule that Roman letters are used for statistics, while Greek letters are used
for parameters. However, the AP exam uses a different notational convention,
which is that 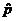 = sample proportion
(statistic), p = population
proportion = probability (parameter). Therefore, you need to translate all
occurrences of p in your textbook
into = sample proportion
(statistic), p = population
proportion = probability (parameter). Therefore, you need to translate all
occurrences of p in your textbook
into 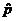 when reading, and
translate all occurrences of when reading, and
translate all occurrences of 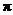 into p. You can make the translation in
your head, or you can mark the changes in your textbook. For tomorrow, you
are required only to make the changes to the tan box on p. 465. Please make
the changes in pencil, in case you wish to sell your used textbook at the end
of the year. into p. You can make the translation in
your head, or you can mark the changes in your textbook. For tomorrow, you
are required only to make the changes to the tan box on p. 465. Please make
the changes in pencil, in case you wish to sell your used textbook at the end
of the year.
|
|
|
Th 1/26/012
|
HW due: Read summary on pp. 469-470; write #8.22,
8.30, 8.37, and the question below.
Question: Why do we care about
sampling distributions? What value could they possibly have?
|
|
|
F 1/27/012
|
HW due: Make sure yesterday’s written work is
complete (matching against worked examples if necessary). Then, read pp.
475-480, 482-484 (middle). In the green box on p. 484, rewrite 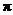 as p and the formula as as p and the formula as 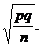
|
|
|
M 1/30/012
|
No additional HW due. Please get plenty of sleep,
recharge your batteries, and do something kind for a stranger.
|
|
|
T 1/31/012
|
HW due: Write review problems on p. 470 (#8.32,
8.33, 8.34, 8.36), plus full corrections of #8.30 and 8.37 from the solutions
listed below.
8.30.
Assume that sample is an SRS of likely voters [must be stated].
Check: Is N 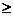 10n? Yes, assuming there are at least
10(500) = 5000 voters in the district. 10n? Yes, assuming there are at least
10(500) = 5000 voters in the district. 
Check: Is np  10? Yes, since
500(0.48) = 240 >> 10. 10? Yes, since
500(0.48) = 240 >> 10. 
Check: Is nq 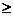 10? Yes, since
500(0.52) = 260 >> 10. 10? Yes, since
500(0.52) = 260 >> 10. 
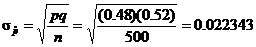
Thus we can use the N(0.48,
0.022343) distribution to approximate the sampling distribution of 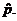
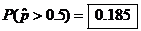 by calc. by calc.
8.37
Assume that the 50 shoppers constitute an SRS of all possible shoppers.
Check: Is population distribution normal? (Doesn’t matter, since n = 50 > 30.)
Check: Is population distribution free of extreme skewness or outliers? (Must
assume!) 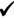
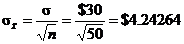
By the CLT, the sampling distribution of 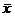 is closely
approximated by N(100, 4.24264). is closely
approximated by N(100, 4.24264).
Total amount spent exceeds $5300 when the mean for all 50 exceeds $5300/50 =
$106.
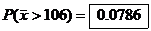 by calc. by calc.
|
|