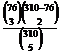|
M 12/12/011
|
HW due: Write definitions of random variable, discrete, continuous, binomial, geometric, and independent trials. Then write #7.62
on p. 397 and the following review problems on pp. 431-434: #7.103, 7.104,
7.105, 7.108, 7.116. Note: In #7.108, you must give a quantitative reason for part
(b), showing work. If you cannot finish all the review problems for today,
then do as many as you can, and finish the rest by Tuesday.
In class: Review for test.
|
|
|
M 12/19/011
|
HW due: No additional written work is due, but read
the paragraphs below.
1. Please use this time to get caught up on any previously assigned problems
that you may have missed on the first pass.
2. Begin studying for your Big Quiz, which will cover all material through
the end of Chapter 7.
3. Transformations to achieve normality are not an AP topic. Therefore, we
will discuss only one of the most useful transformations to achieve
normality, namely the logarithm, which is involved in lognormal
distributions. Lognormal distributions are simply distributions whose
logarithms follow a normal distribution. Many real-world phenomena—income,
wealth, and the size of cities, to name a few—can be modeled by lognormal
distributions.
4. To check to see whether a distribution complies with a “lognormal” shape,
we will (1) store the data in L1, (2) store the log of the data in
L2 (keystrokes are log(L1) STO L2 ENTER),
and (3) create a normal quantile plot for the data
in L2. If the pattern is close to a straight line, then we have
good evidence that the original data in L1 were lognormal.
|
|
|
T 12/20/011
|
HW due: Answer review problems 1-7 listed below.
1. Identify each of the following random variables as discrete or continuous.
You do not need to write the questions for #1, but you do need to write the word “discrete” or “continuous” each time in
order to practice your spelling.
(a) age (to the nearest year) of a randomly selected citizen of the District
of Columbia
(b) diameter of a peg turned on a lathe by a peg-making machine
(c) snowfall (in inches) at a randomly selected location on earth on a
randomly selected day
(d) number of students present at table 36 in the refectory on a randomly
selected school day
(e) number of free throws a basketball player must take in order to sink 2 in
a row
(f) weight (to the nearest 0.5 lb.) of a randomly chosen student when weighed
on a digital scale
(g) weight of a randomly chosen student
(h) SAT math score of a randomly chosen student
(i) mean SAT math score for the U.S. in a randomly
chosen year, past or future
2. Mr. Wilson selects 5 Upper School students at random to form a focus
group. Let X denote the number of
Form VI students who happen to be chosen to be part of the focus group. There
are 310 Upper School students, 76 of whom are in Form VI.
(a) Explain why X
is not a binomial random variable.
(b) Explain why it is nevertheless acceptable to
treat X as a binomial random
variable. Hint: Compare the
probability of selecting a senior for the 5th slot if no other seniors have
been previously chosen, compared to the probability of selecting a senior for
the 5th slot if all 4 previous slots have been filled by seniors.
(c) List the sample space of possible outcomes for X, along with their associated probabilities.
(d) The set of all possible outcomes for a random variable, along with their
associated probabilities (or probability densities, in the case of a
continuous r.v.) is called a
____________________________ (hint:
starts with the letter D) and is usually depicted by means of a
__________________ __________________ __________________ (hint: letters R, F, H) or a
__________________ curve. We use the former depiction for __________________
random variables, the latter depiction for __________________ random
variables.
(e) Compute the probability that fewer than 3 seniors are chosen.
(f) Compute the probability that exactly 1 or 2 seniors are chosen.
(g) Compute the probability that at least 1 senior is chosen.
(h, i, j) Repeat parts (e), (f), and (g) using exact probabilities, not the binomial
approximations. For example, the exact probability of choosing exactly 3
seniors is
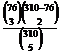 = 0.0830, which is
quite close to the binomial probability of = 0.0830, which is
quite close to the binomial probability of 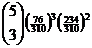 = 0.0840. = 0.0840.
3. There are about 600,000 people in Washington, DC, of whom approximately 2%
are HIV-positive. If you shake the hands of randomly chosen DC residents, one
by one, let Y denote the number of
hands you need to shake in order to encounter an HIV-positive individual.
(a) Explain why Y
is not a geometric random variable.
(b) Is it acceptable to treat Y as
if it were geometric? Why or why not?
(c) Compute the mean of Y.
(d) Use your calculator to estimate the standard deviation of Y. Store values of p and q as P and Q, respectively. Then use the first 200 entries of the
distribution and run 1-Var Stats on your lists. To create lists L1
and L2, you can use the keystrokes 2nd LIST OPS seq(X,X,1,200,1) STO L1 ENTER, followed by 2nd
LIST OPS seq(PQ^(X-1),X,1,200,1) STO L2
ENTER.
(e) The exact variance of Y is
given by the formula q/p2. Compute this value, and
then compute the s.d. from that. How close did you
come in part (d)?
(f) Compute the probability that the first HIV-positive person whose hand you
shake is person 40 or later.
(g) Compute the probability that the first HIV-positive person whose hand you
shake is strictly after person 13
but strictly before person 77.
4. Mr. Hansen’s latest SAT alternative test (the HAT, or Hansen Aptitude
Test) has a mean of 550 and a s.d. of 90. Scores
are approximately normally distributed. Compute
(a) the 70th percentile of the HAT
(b) the proportion of test takers who score between 580 and 640
(c) the HAT score that corresponds to an SAT score of 700
(d) the cutoff HAT scores that capture the central 85% of the distribution.
5.(a) In #4, why is it necessary to specify that the
HAT has an approximately normal distribution?
(b) Give the standard abbreviation for the HAT distribution.
6.(a) Show that the following data set is approximately normally distributed:
{92, 95, 59, 64, 72, 75, 77, 79, 81, 83,
88, 91, 79, 82.5, 83, 94}
(b) Is there any skewness evident in part (a)? If
so, what type?
7.(a) Show that the following data set is not
normally distributed:
{24, 25, 4, 5.5, 6, 8, 8.5, 10, 11, 12,
14, 16, 14, 11, 12, 18}
(b) Show that the data set in part (a) is approximately lognormal.
(c) Would it surprise you to learn that the data in part (a) come from a list
of city populations (in thousands)? Why or why not?
In class: Review
|
|