|
M 10/3/011
|
HW due:
1. Read pp. 117-124, 127-133, 135-136.
2. Write #3.56 on p. 138.
3. Commit your group’s data-gathering instrument (either a survey or a uniform
script to be used when polling your subjects) to writing, and submit this at
the start of class. Group 1 has a different requirement, since they will be
using texts from volunteers. Group 1 should submit a list of subjects
recruited so far.
|
|
|
T 10/4/011
|
HW due:
1. No additional group project HW. Because of yesterday’s fire drill, we did
not have time to go over the survey instruments yet. Although you can run a
pilot test if you wish, do not do any formal data gathering yet.
2. Read pp. 147-156, 159-166. Especially read the starred footnote at the
bottom of p. 156. We will use the notation of “some statistics books”
throughout the year: p (not 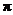 ) for the population proportion, and ) for the population proportion, and 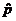 (pronounced “p-hat”)
for the sample proportion. The reason we do this is that we would prefer to be
compatible with the notation used on the AP exam. Simply be aware that when
your textbook uses the symbol for pi, you should instantly translate that
into p for population proportion. (pronounced “p-hat”)
for the sample proportion. The reason we do this is that we would prefer to be
compatible with the notation used on the AP exam. Simply be aware that when
your textbook uses the symbol for pi, you should instantly translate that
into p for population proportion.
3. Write #4.4, 4.24.
|
|
|
W 10/5/011
|
HW due:
1. Project leaders will receive an e-mail with suggested revisions to the
survey instrument. You may then begin gathering data if you wish. Deadlines
will be discussed in class. Because we have a 4-day weekend coming up, the
due date will not occur next week.
2. Read pp. 169-174, 176-183.
3. Write #4.30 on p. 175.
|
|
|
Th
10/6/011
|
HW due:
1. Begin gathering data for your group project.
2. Prepare a raw data spreadsheet and bring a printout of your spreadsheet to
class. At a minimum, even if you have
not successfully contacted any test subjects yet, you must have an Excel
spreadsheet laid out with field names in row 1 and column headings in columns
A, B, C, D, etc. Cell A1 should say “Subject ID,” and cell B1 should say
“Subject Name.” Other columns would have variable names for the other data
items that you are gathering. For example, cell C1 might say “ZIP Code,” and
cell D1 might say “Party Affiliation.” In cell A2 you would type the number
1, in cell A3 you would type the number 2, and so on for each of your test
subjects. Bring a printout of your Excel spreadsheet to class, in whatever
state it may currently be in.
3. Read pp. 186-189, 191-192.
4. Write #4.60 and #4.69 on pp. 194-195.
|
|
|
F 10/7/011
|
No school.
|
|
|
M 10/10/011
|
No school.
|
|
|
T 10/11/011
|
HW due:
1. All groups except Bogdan’s group must e-mail Mr.
Hansen the Excel file requested last Thursday. (Bogdan’s
group is exempt because they already turned in a hard copy.)
2. Read pp. 199-207.
3. Write #5.1abcdefghi, where part (i) is to
estimate the correlation between height and income.
4. Write #5.10abc. In part (a), be sure to make a rough copy of the scatterplot on your HW paper.
5. Write #5.12 abc. In part (a), be sure to make a
rough copy of the scatterplot on your HW paper.
|
|
|
W 10/12/011
|
Review day; no additional written HW due. However,
all previously assigned problems (including any from yesterday’s assignment
that you may not have been able to complete) are expected to be complete by
now. A spot check of HW may be conducted.
The “Quick Study” quiz that would normally occur today will instead be
included on tomorrow’s test. You may use handwritten notes (maximum of one
standard-size sheet of paper) during the test.
|
|
|
Th
10/13/011
|
Test (100
pts.) on Chapters 3 and 4, plus §5.1, plus everything discussed in class
(including notation) since the beginning of the year.
The test will also include a question or two based on last
week’s Quick Study in the Post
issue of 10/3/2011. You may use
handwritten notes (maximum of one standard-size sheet of paper) during the
test. Notes on items unrelated to the Quick Study are also permitted, for
this test only.
During the test, you will be provided with a standard set of AP formula
sheets (pp. 12-16 at this
site, but note that if you print them out, you need to request pp.
16-20). One useful formula that is not provided there is the formula for
computing a z score:
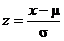
As we discussed in class on 10/12, this formula tells you the number of standard deviations that a
data point (namely x) lies to the
left or right of the mean. A positive z
score indicates that x is above the
mean, whereas a negative z score
indicates that x is below the mean.
|
|
|
F 10/14/011
|
No additional HW due. However, previously assigned
problems may be re-scanned or spot checked.
|
|
|
M 10/17/011
|
HW due: Group leaders will give a brief oral status update.
(See below for particulars.)
You should meet over the weekend with your group members, either in person or
electronically, to discuss your strategy for your group project writeup. Projects are due Friday, 10/21, at 3:00 p.m.
Also, one group still owes me an empty raw data spreadsheet, which was due on
Tuesday, 10/11.
Group 1: Browning, Kieran, Sam
Group 2: Miles, Frederik, Mr.
Hansen
Group 3: Bogdan, Nathan, Joe
Group 4: Matt, Karl, Steven
By now you should have gathered at least some of your data. If not, plan to
assign data collection duties for Monday and Tuesday.
The project writeup will probably be 3 to 5 pages
long, plus your raw data table as an appendix. NOTE: A printout of the raw data table is required. The “3 to 5
pages” is only a rough guideline, not a requirement. Do not think that you
have to write 3-5 pages of text; graphs and tables will take up at least half
the space in your report. As was explained last Friday, an “A” project can be
as short as a page or two, and a 10-page project with tons of gratuitous
color graphics and boring “filler” text may not even earn a passing grade.
Computer graphics are not required; hand-drawn graphics are acceptable.
Group leaders are required to submit a report stating what each person did (a
concrete list of tasks), plus a recommended division of points. Equal point
splits are common but by no means universal. Point splits must be justified
by the description of what each person did, not by vague generalities such
as, “Everyone worked diligently on this project and deserves an equal point
split.”
Finally, remember that this is the 21st century. Spelling and grammar
mistakes in your final report are really not acceptable, since you can and should
be using a computer to help catch all of those problems. You may also submit
a draft copy for review and suggestions as a way of improving your grade.
|
|
|
T 10/18/011
|
HW due:
1. Read pp. 210-217, 221-228. Note:
Ignore the tan box on p. 213, and ignore the final tan box on p. 228.
2. Write #5.28 on p. 220.
3. Continue working on your group project, which is due at 3 p.m. on Friday,
10/21.
|
|
|
W 10/19/011
|
HW due:
1. Read pp. 238-245.
2. Write #5.38 and 5.40 on pp. 234-235.
3. Continue working on your group project, which is due at 3 p.m. on Friday,
10/21.
|
|
|
Th
10/20/011
|
HW due: Work on your group project, and get enough
sleep to build up more positive
learning energy.
|
|
|
F 10/21/011
|
HW due:
1. Work on your group project, which is due at 3 p.m. today. Please read the
10/17 calendar entry for additional instructions.
2. Yesterday we proved that if the log of y
is linearly related to x, and if we
know the intercept (b0)
and slope (b1) of that linear
model, then we can compute an exponential function that allows us to predict y as a function of x. In a similar fashion, prove that if
the log of y is linearly related to
the log of x, then we can predict y as a power function (PwrReg) of x. If your algebra is good, this proof
should take you about 5 minutes. If not, please ask a classmate for some
suggestions! (This homework assignment is due at the start of class.)
|
|
|
M 10/24/011
|
HW due:
1. Group projects are granted a penalty-free extension until 3 p.m. today.
2. Read from middle of p. 249 (“Power Transformations”) through p. 252.
3. Read chapter summary, pp. 268-269. Ignore the formulas for b, SSResid, SSTo, se
and the logistic regression equation.
4. Write #5.74 on pp. 271-272.
|
|
|
T 10/25/011
|
Test (100
pts.) through Chapter 5. Test will be held in MH-102 (normal classroom) at
9:00.
For this test, you will be able to “punch the buttons” to achieve nonlinear
regression equations if necessary (ExpReg, PwrReg, etc.). We will hold off doing the more
complicated subject of “transformations to achieve linearity” until later.
However, you are expected to know
that the hallmark of exponential regression is that “log y is an approximately linear function of x” and that the hallmark of power regression is that “log y is an approximately linear function
of log x.” Moreover, you are
expected to be able to prove that one of these linear fits is valid, and it
is not enough simply to write down
a high r2 value. For
full credit, you must also sketch the residual plot and explain why it proves
that a linear fit is appropriate.
|
|
|
W 10/26/011
|
No additional HW is due today. However, older
problems may be re-scanned. Bring all equipment to class, as always: pencil,
calculator, textbook, 3-ring binder.
|
|
|
Th
10/27/011
|
HW due:
1. Read pp. 279-286. Note that we will use the notation ~A for the complement of event A,
instead of the various notations proposed in #1 from the tan box on p. 283.
2. Then write #6.10 and #6.12 on pp. 287-288. A tree diagram is required for
#6.10a.
3. Note that for #6.12, you are proving De Morgan’s Laws: 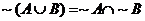 , and , and 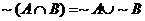 . .
|
|
|
F 10/28/011
|
HW due:
1. Read pp. 289-299.
2. Store the following definition in your brain: Probability = long-run relative
frequency.
3. Write #6.20 and 6.23 on p. 301. Use “P”
notation; do not simply write down
answers. For example, for #6.23d, you would write your answer as follows:
6.23(d) P(exactly 3 receive their
own bks.) = 0 since the fourth is determined by process of elimination
|
|
|
M 10/31/011
|
HW due:
1. Read pp. 302-310.
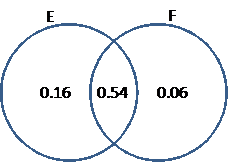
2. Write #6.28*, 6.30, 6.33.
* Before beginning #6.28, copy the following Venn diagram into your notes and
explain why it is valid.
|
|
