|
M 4/2/012
|
No class.
|
|
|
T 4/3/012
|
No additional HW due today.
|
|
|
W 4/4/012
|
HW due: Write Activities 12-5, 12-6, and 12-7 on pp.
251-253.
|
|
|
Th
4/5/012
|
HW due: Write Activities 12-8, 12-9, 12-10, and
12-22 on pp. 253-257.
|
|
|
F 4/6/012
|
HW due: Read pp. 319-323 and answer all of the
questions on those pages.
|
|
|
M 4/9/012
|
No class.
|
|
|
T 4/10/012
|
HW due: Read pp. 324-326, plus the first paragraph
of p. 327, and answer all questions on those pages.
Note: This material is somewhat
more difficult than what we have been doing. I expect to see some visits
during D period Monday, after school Monday, etc. If you don’t visit or at
least send an e-mail with some specific
questions, you will be expected to have all the answers correct when homework
is checked today.
Example of a specific question:
“Mr. Hansen, in question q on p. 326, I assume that when the book says to
solve algebraically for the sample size n,
the intention is to set the m.o.e. to 0.01 and
solve for n. However, the only
formula I can find for m.o.e. is on p. 322, where
it looks as if the m.o.e. must be the thing that is
being ‘added or subtracted,’ namely 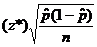 . And, I assume I get z*
from the critical value table on p. 324. Are my assumptions correct?”
Answer: Yes. You can also use the
bottom row of the critical value table on p. 631.
Example of a nonspecific question:
“Mr. Hansen, in question q on p. 326, I don’t understand. Could you tell me
how to answer the question?”
Answer: Sorry, but no. However, if
you reformulate your question in a more specific manner, we’ll talk.
|
|
|
W 4/11/012
|
Career Day (no class). Be sure to come in after
school today (before 3:30 p.m.) if you need help.
|
|
|
Th
4/12/012
|
HW due: Assignments due 4/5, 4/6, and 4/10 may be spot-checked
or collected. All three of these assignments should now be complete. Come in
after school Wednesday (before 3:30 p.m.) if you need help.
|
|
|
F 4/13/012
|
HW due: Get caught up on all previously assigned
problems, and complete the problems listed below.
Given: Mr. Myers’ tests follow the N(86,
6) distribution, while Mr. Hansen’s tests follow the N(77, 10) distribution.
(a) A student scores 72 on a test written by Mr. Myers. What is the student’s
percentile?
(b) Which is “better”: a 69 on a Mr. Hansen test, or a 69 on a Mr. Myers
test?
(c) What percentage of students score between 79 and 90 on Mr. Myers’ tests?
(d) What scores give the central 50% of students for Mr. Hansen?
(e) What scores give the central 50% of students for Mr. Myers?
Note: Questions (d) and (e) are
asking about the Q1 and Q3 cutoffs. From these, you
could easily compute the IQR for each teacher.
|
|
|
M 4/16/012
|
No class.
|
|
|
T 4/17/012
|
No class (Diversity Day).
|
|
|
W 4/18/012
|
Review for test. No additional HW is due, but any
older assignments may be checked. Be sure you are up to date!
|
|
|
Th
4/19/012
|
Test (100
pts.) on all recent material.
To help you prepare for the test, the following answers to last Friday’s HW are
provided:
(a) 0.98 percentile (approximately the 1st percentile, with 99% of students
scoring higher)
(b) A 69 on a test in Mr. Hansen’s class is better, because it has a higher z-score (–0.8 as compared to –2.833).
Or, you could compare percentiles: 21st percentile is
better than the 0th percentile.
(c) 62.6%
(d) 70.26 to 83.74 (use invNorm(.25), multiply by s.d., add to mean; then repeat for 0.75)
(e) 81.95 to 90.05
|
|
|
F 4/20/012
|
HW due: Write Activity 16-5 on pp. 329-330. You may
need to research the 1936 election (and/or Alf Landon and Franklin D.
Roosevelt) when answering part (c).
|
|
|
M 4/23/012
|
No school.
|
|
|
T 4/24/012
|
HW due: Come up with a reasonable estimate for the
probability of obtaining at least one roll of “6” when rolling a fair die 6
times. Show work. No credit for grossly wrong answers.
|
|
|
W 4/25/012
|
HW due: A fair coin is flipped 10 times. What is the
probability of having a run of at least 4 heads or 4 tails in a row? Show
work. No credit for grossly wrong answers.
|
|
|
Th
4/26/012
|
HW due:
1. Make a scatterplot (notional) of time spent
sleeping on the x-axis and calculus
GPA on the y-axis.
2. Estimate the linear correlation coefficient (r value) in your scatterplot from #1.
3. Make a list of 3 or more quantitative variables that are positively
correlated with hours of sleep, and estimate the r value in each case.
4. Make a list of 3 or more quantitative variables that are negatively
correlated with hours of sleep, and estimate the r value in each case.
|
|
|
F 4/27/012
|
HW due:
1. Visit www.cars.com and choose a late-model used car that you might be
interested in owning. Gather 20 or more ordered pairs of data (odometer
reading and asking price) from cars that are reasonably similar to each
other. The cars do not need to be identical, but they should preferably all
be of the same model year and should be similar enough that the price
comparison is roughly valid. You may need to enlarge your search radius
beyond the default value of 30 miles in order to find enough data points. On your
HW paper, record the model year, make, model, and other relevant information
(such as body style, 2-door vs. 4-door, etc.) that you are using in order to
gather your data.
2. Write your ordered pairs in a table. Label the columns appropriately (x and y are helpful but are not sufficient by themselves).
3. Enter the explanatory variable in L1 and the response variable
in L2. Perform a linear regression (STAT CALC 8) and write the
values for a, b, and r, along with
their identifiers. Follow the pattern below. Write out all lines fully; do
not simply fill in the blanks.
a = intercept = _______________
b = _______ = _______________
r = _____________ correlation
_____________ = _______________
4. What percentage of the variation in asking price can be explained by
variation in mileage? Show your work.
5. Write the linear model in the form 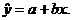 (Write numbers for a and b, but use letters for x
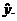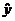and  ) Important: Be sure to define what x and  stand for, in plain
English.
6. Use your linear model to predict the asking price for a car with 43,500
miles on the odometer. Show work as demonstrated in class yesterday.
7. Use your linear model to predict the asking price for a car with some
number of miles, other than 43,500, that is well within the domain of x values for which you have gathered
data. Show work as in #6.
8. How much confidence (low, medium, or high) do you have in your answer for
#7?
9. Use your linear model to predict the asking price for a car with 280,000
miles. Show work as in #6.
10. How much confidence (low, medium, or high) do you have in your answer for
#9? Explain briefly.
|
|
|
M 4/30/012
|
No class. Mac, please re-do Friday’s assignment and
see me during F period.
|
|