|
W 1/18/012
|
First day of class.
|
|
|
Th
1/19/012
|
HW due: Order our
textbook from Amazon.com or any other provider of your choice.
|
|
|
F 1/20/012
|
No additional HW due. However, review your class
notes (or rethink what we discussed about categorical data, quantitative
data, variables, mean, mode, and median), since another pop quiz is possible.
|
|
|
M 1/23/012
|
No class.
|
|
|
T 1/24/012
|
HW due:
1. Bring in a newspaper or magazine clipping in which the central issue is a
statistical controversy. (Don’t just bring in an article containing
statistics; almost every article has at least one statistic of some sort.
Instead, focus on finding an article in which the way statistics are
computed, or the meaning of statistics, or the quality of
the underlying data are being disputed.)
2. Review your notes concerning Q1, Q2, Q3,
IQR, 5-number summary, min, max, range, mean (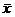 ),the rule for determining outliers, and the calculator
method for calculating statistics (STAT 1-Var Stats) from a column of data.
Another open-notes quiz is possible. ),the rule for determining outliers, and the calculator
method for calculating statistics (STAT 1-Var Stats) from a column of data.
Another open-notes quiz is possible.
|
|
|
W 1/25/012
|
HW due:
1. Same as assignment #1 from yesterday. Find an article in which statistics
are not merely presented but are under attack. For example, some group may be
claiming that some other group’s facts are inconclusive because the data are
only “anecdotal,” not scientifically gathered.
2. Suppose that there are 25 boys in a class. We wish to estimate their mean
height without sampling everyone, and we will use a random sample of size 10
to do that. Use a random number generator, a spinner, or slips of paper drawn
randomly from a hat in order to choose your sample of 10 boys. Then, use the
techniques shown in class last Friday (STAT EDIT plus STAT CALC 1-Var Stats)
to compute the mean and standard deviation of your sample. In your homework,
be sure to indicate which 10 boys you chose randomly.
Write your answers in the following format:
sample mean = 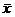 = __________ inches = __________ inches
sample standard deviation = s =
__________ inches

|
|
|
Th
1/26/012
|
HW due: For the data set given in yesterday’s
assignment, compute the value of 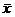 for a random sample
of size 5. Use your calculator’s random number generator (or draw slips of
paper from a hat) to determine who is in the sample, and record an
abbreviation of the boys’ names. Here is an example of what you should write: for a random sample
of size 5. Use your calculator’s random number generator (or draw slips of
paper from a hat) to determine who is in the sample, and record an
abbreviation of the boys’ names. Here is an example of what you should write:
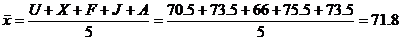
(a) Plot the value of 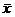 on a number line. Then
repeat the process 6 more times, each time using a random sample of size 5.
(We say that 5 is the sample size, or n
= 5. Note that 5 is not the number
of on a number line. Then
repeat the process 6 more times, each time using a random sample of size 5.
(We say that 5 is the sample size, or n
= 5. Note that 5 is not the number
of 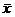 values that you are
plotting.) When you are finished, you should have 7 points graphed on your
number line. Show your work each time as illustrated above. values that you are
plotting.) When you are finished, you should have 7 points graphed on your
number line. Show your work each time as illustrated above.
(b) Now draw 7 random samples of size n
= 13, and write down the value of 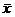 each time. Since
this part of the exercise will take longer, you do not need to record the
names of the boys used in these 7 samples. On a number line that matches up
directly underneath the one you drew in part (a), mark the 7 values for each time. Since
this part of the exercise will take longer, you do not need to record the
names of the boys used in these 7 samples. On a number line that matches up
directly underneath the one you drew in part (a), mark the 7 values for 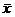 that you obtain. that you obtain.
(c) Which number line has readings that are more spread out, (a) or (b)?
(d) Before you performed the exercise, which number line did you expect to
have its readings more spread out, (a) or (b)?
(e) Why were you expecting the result you predicted in (d)? Did the results
turn out the way you expected?
|
|
|
F 1/27/012
|
HW due:
1. Learn to state the more formal version of the Central Limit Theorem,
including the fact that the sampling distribution of 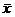 has standard deviation
approximately equal to has standard deviation
approximately equal to 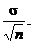 There may be a quiz. There may be a quiz.
2. Calculate the standard deviation of 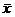 in each of the
following situations. You are not allowed to assume that the populations have
bell-shaped normal distributions. Be sure to show your work. in each of the
following situations. You are not allowed to assume that the populations have
bell-shaped normal distributions. Be sure to show your work.
(a) Sample mean = 38.2, population s.d. = 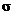 = 14.8, sample size
= 35. = 14.8, sample size
= 35.
(b) Sample mean = 17.9, population s.d. = 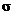 = 3.1, sample size =
84. = 3.1, sample size =
84.
(c) Sample mean = –2.18, population s.d. = 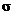 = 0.82, sample size
= 22. = 0.82, sample size
= 22.
3. The central 95% of any bell-shaped normal distribution will extend 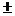 2 standard deviations from the mean. Compute a 95%
confidence interval for the true population mean, 2 standard deviations from the mean. Compute a 95%
confidence interval for the true population mean, 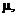 in each of the
situations given in #2. Use the approved wording given in class: “We are 95%
confident that . . .” in each of the
situations given in #2. Use the approved wording given in class: “We are 95%
confident that . . .”
|
|
|
M 1/30/012
|
No class.
|
|
|
T 1/31/012
|
HW due: Read the following paragraph and answer the
questions that follow.
The bell-shaped normal distribution appears so often in nature and in the
real world that we have a special notation for referring to it. The normal
curve with mean a and standard
deviation b is abbreviated N(a, b).
For example, N(5,7)
denotes a bell-shaped normal curve with mean 5 and standard deviation 7, and N(–45, 3) denotes a bell-shaped normal
curve with mean –45 and standard deviation 3. The standard deviation is
always positive, but the mean can be positive, negative, or 0.
The central 68% of any bell-shaped normal curve will occur between the places
where the curvature of the bell switches from upward to downward and from
downward to upward. These are called the inflection
points of the curve.
Sketch each of the following distributions, labeling the mean and the
inflection points on your x-axis
for each sketch.
1. N(5,7)
2. N(–45,
3)
3. N(69,
3)
The last distribution is approximately the distribution of the heights of
American men (in inches). About 95% of the data in any normal distribution
will occur between plus or minus 2 standard deviations of the mean.
4. What are the cutoffs for heights that contain approximately the central
95% of American adult males?
|
|
