|
W 1/18/012
|
First day of class.
|
|
|
Th
1/19/012
|
HW due: Download the Java textbook to
your hard drive, and read the Preface (pp. v-ix) and the first part of
Chapter 1 (pp. 1-5). Modest reading notes are required each day; see the HW guidelines
for the required format.
|
|
|
F 1/20/012
|
HW due:
1. Download and install the integrated development environment (IDE) for Java
from www.eclipse.org. Download the regular Java
compiler, not the Java EE compiler. It is important for you to choose the
correct version (32-bit or 64-bit); read this
Microsoft article if you do not know how to tell
which version of Windows you are running.
2. Read through the end of Chapter 1 (p. 11).
3. Write Exercise 1.1 on p. 11 (all 3 parts).
4. (Optional) Perform Exercise 1.2. If you do not have time to do this, don’t
worry, because we will do it in class, together. However, you will have a
head start on the rest of the class if you can do it at home.
|
|
|
M 1/23/012
|
HW due:
1. Read Chapter 2 (through p. 22), and make some reading notes, as always.
2. Write up your answers to Exercise 1.2 on the 3-hole-punched sheet that was
handed out in class on Friday. Put your name in the upper right corner. For
example, if the change results in an error message, write the text (or at
least an abbreviated version of the text) that appears on the console screen
as an error message. If no message appears, describe the action that does
occur.
|
|
|
T 1/24/012
|
No class.
|
|
|
W 1/25/012
|
HW due:
1. (Jackson only) Visit www.asciichart.com
and click “Hexadecimal” at the top of the page so that you can see what the
rest of the class learned about hexadecimal codes for ASCII characters. ASCII
= American Standard Code for Information Interchange.
1. (Everyone else) Prepare to teach Jackson about “bits, bytes, hex, and
Hertz.” Mr. Hansen will sit in the back of the classroom and will cough or
interrupt when something incorrect is said. Everyone will have to pull his or
her weight!
2. (Everyone, including Jackson) Use www.asciichart.com
and click “Hexadecimal” at the top in order to decode the following hex data
into text. Be sure to distinguish upper case from lower case letters. The
prefix “0x” merely denotes that the data are in hex;
it is not part of what you are decoding. The hex byte 20, when it appears
below, signifies a space.
0x4950
0x4C20
0x6973
0x204F
0x2E4B
0x2E21
3. (Everyone except Jackson) Reinterpret the data above as 6 two-byte
integers. Show your work. The first one is solved for you as an example.
0x4950 = 4(163) + 9(162) + 5(161) + 0(160)
= 4(4096) + 9(256) + 5(16) + 0 = 16,384 + 2304 + 80 = 18,768
|
|
|
Th
1/26/012
|
HW due:
1. (Jackson only) Do #3 from yesterday.
2. (Everyone) Write the following message in Unicode. Remember to put the
prefix “0x” at the beginning.
Java uses a bytecode
compiler.
3. (Everyone) Unicode, a 2-byte code, supports 65,536 different symbols, from
0x0000 through 0xFFFF. However, imagine that in the year 2112, Unicode is
found inadequate to support the world’s information processing needs. How
many different text symbols could be represented in a 3-byte code? ______
What about in a 4-byte code? ______
4. (Everyone) A hash function is a
function y = f (x) in which x, the input, is a file of any length,
and the output, y, is a
software-generated value having a certain fixed number of bits. Good hash
functions are extremely unpredictable, in the sense that any small change to x causes approximately half the bits
of y to change. What is the probability
that by chance alone, 2 different files, x1
and x2, both produce the
same output value y, given that y = f (x) is a 32-bit hash
function?
|
|
|
F 1/27/012
|
HW due:
1. Without referring to your class notes (unless absolutely necessary), write
the truth tables for the AND, OR, XOR, NAND, and NOR gates. Each table should
have a heading row plus 4 additional rows: a row where A = 1 and B = 1, a row
where A = 1 and B = 0, a row where A = 0 and B = 1,
and a row where both A and B are 0 (false).
2. How many rows would a truth table need in order to show all possible
states for 5 inputs labeled A, B, C, D, E, and F?
3. Logical implication, which Karl mentioned briefly yesterday, is defined by
the following truth table:
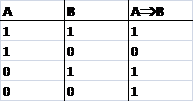
Show that the “implication” gate has exactly the same outputs for all
possible values of A and B that you would get by computing ~A OR B (that is,
the negation of A, ORred with the value of B).
4. Use a clever combination of nothing but NAND gates in order to produce a
circuit that works exactly like an OR gate. You are allowed to use as many
NANDs as you wish, and you may connect them in any way you wish.
|
|
|
M 1/30/012
|
Whenever the lead digit of a signed hex integer is 8
or greater, the number is to be interpreted as negative number. The natural
question to ask is, “Which negative number?” The answer is found by taking
the 2’s complement (bit-flip and add 1).
Example: In a dword format, 0x7FFFFFFF is the largest
possible positive integer, and 0xA432B7CE is negative, since the lead digit,
A, is 8 or more. To convert 0xA432B7CE to a signed decimal integer, we
bit-flip to obtain the 1’s complement (namely, 0x5BCD4831) and add 1. The
result, 0x5BCD4832, is the 2’s complement of 0xA432B7CE, and it should be
interpreted as the negative of 5(167)
+ 11(166) + 12(165) + 13(164) + 4(163)
+ 8(162) + 3(161) + 2(160) = 1,540,180,018.
Final answer: –1,540,180,018.
HW due: Perform each addition or subtraction using 2’s complement addition arithmetic. Give answer in
both hex and decimal. Remember, subtraction means adding the 2’s complement,
and any negative number must be rendered (and, if in the answer, interpreted)
using the rules of 2’s complement arithmetic. If an overflow condition occurs
(e.g., positive + positive = negative, or negative + negative = positive), be
sure to state that. You may use the Windows calculator (calc.exe) in View /
Programmer mode to check your answers. Use dword
(4-byte) format throughout, and SHOW YOUR WORK NEATLY.
1.
0xFACEB00C
+ 0x00000709
2.
0x00000048
– 0x00000032 (do not subtract; instead, add the 2’s complement)
3.
0x19338A0D
– 0x463A2CE4 (again, do not subtract; instead, add the 2’s
complement)
4.
0x639B13AC
+ 0x5399E01F
5.
0xB30F13B5
+ 0xC3A9E41C
|
|
|
T 1/31/012
|
Class for Jackson, Andrew, and Danielle only.
Tomorrow’s review problems will be posted by 3 p.m. today.
|
|
