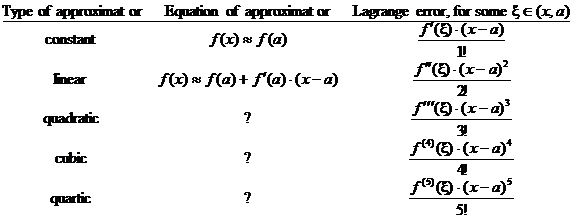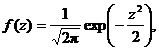|
M 4/2/012
|
Classes resume. No additional HW due.
|
|
|
T 4/3/012
|
HW due: Read §12-8; write #Q1-Q10 on p. 646. We need
to “ease back” into the swing of things!
|
|
|
W 4/4/012
|
HW due: Read the material below; write §12-8 #3, 4,
5, except that for #5, compute sin 2
instead of sinh 2, and perform the work for #5
using both the Lagrange error bound and the AST error bound.
Note: When your textbook says
“accuracy to 6 decimal places,” read that to signify |error| < 0.0000005.
You won’t have to worry about this on the AP exam, since the desired accuracy
will always be specified as a value there, not as a number of decimal places.
In the spirit of yesterday’s discussion, please consult the table below and
fill in the 3 missing cells.
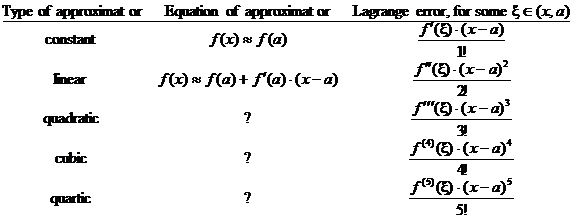
|
|
|
Th
4/5/012
|
HW due:
1. Write §12-8 #6. You are encouraged to read the worked solution under the 4/13/2009 calendar entry.
2. Finish yesterday’s assignment if you have not already done so. Suggestion: Use n consistently to denote the degree of the Taylor polynomial
used, so that n + 1 is always the degree of the error term. Note that the
“number of nonzero terms needed” may then be n + 1, n, n/2, or some other expression,
depending on the nature of the series, after you have solved an inequality
involving a bound on the (n + 1)st derivative, a bound on |x – a|n + 1,
and a manually computed denominator of (n
+ 1)!
3. Write §12-8 #14, 15, 16.
|
|
|
F 4/6/012
|
HW due: Write #R7abcdefghjk and #R8de on pp.
651-652.
|
|
|
M 4/9/012
|
HW due: Write solutions to the following review
problems.
·
p. 592 #R2-R3
·
p. 653 #T1
·
p. 654 #T11-T15
all
·
p. 657 #8-9
·
p. 658 #23-24
If you are unable to complete all the problems, then keep a careful time log
and finish the rest before Tuesday.
|
|
|
T 4/10/012
|
Test (100
pts.) on Chapters 11 and 12. Important: Bring your notebook to the test
for a homework grade. The review problems may be spot-checked for
completeness. If they are not all in order, please make a prominent marking
on the first page stating that.
|
|
|
W 4/11/012
|
Form VI (seniors) will not be in class today because
of Career Day. However, HW #3 (see below) is still due today from everyone.
HW due:
1. From now until further notice, bring your AP review book to class each
day, not your main textbook.
2. Write problem #6 from the last
page of this College Board document, and after writing it up, correct
your answers by using a different color of pencil or pen. The easiest way to
do this is to make a printout only of p. 7 and then fold it so that you
cannot see the answer key while doing your work.
3. Submit your review problems (see 4/9 calendar entry) either at the
beginning of class or by slipping them under Mr. Hansen’s office door
sometime later in the day. Deadline is 3:30 p.m. sharp.
|
|
|
Th
4/12/012
|
HW due: Print out the AP review log and start working
(and logging) review problems from your AP review book.
|
|
|
F 4/13/012
|
HW due: Log another 25 minutes’ worth of AP review
problems, and spend your final 10 minutes on the following problems.
The standard normal probability density function (2nd DISTR normalpdf on your calculator) follows the equation 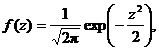
where z is an independent variable
denoting the number of standard deviation units left or right of the mean. A positive value for z
indicates a score higher than the mean, and a negative value for z indicates a score lower than
the mean. The probability of being between any two given z-score values is simply the area under f (z) between those
bounds, and the normalcdf function (cumulative
density function) on your calculator is used to compute the definite integral
of the normalpdf function.
For example, what is the probability that a randomly chosen student will
score between 400 and 680 on the SAT I math portion? The test has a mean of
about 500 and a standard deviation (s.d.) of about
100, which means that the z-scores
are –1 and 1.8, respectively. The probability is 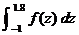 . .
1. Use MATH 9 to compute the given definite integral.
2. Use normalcdf(–1,1.8) to compute the same probability. How do the
answers compare?
3. Which one runs faster: #1 or #2?
4. Compute the antiderivative of f (z).
Be careful!
5. Use your answer from #4 to estimate the probability described above. Show
work.
6. Explain your answer to #3 by speculating how the normalcdf
function was programmed by the TI firmware engineers.
|
|
|
M 4/16/012
|
HW due: 35 minutes of AP problems (logged on your
sheet), plus a revisiting of problems 1-6 from last Friday, which nobody did
very well.
|
|
|
T 4/17/012
|
HW due: AP review log, at least 35 minutes’ worth.
|
|
|
W 4/18/012
|
HW due: AP review log, at least 35 minutes’ worth.
|
|
|
Th
4/19/012
|
HW due: AP review log, at least 35 minutes’ worth.
|
|
|
F 4/20/012
|
HW due: AP review log, at least 35 minutes’ worth.
|
|