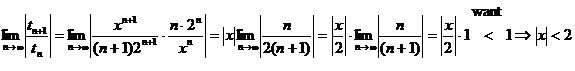|
Th 3/1/012
|
HW due: Write §11-2 #5 (optional), 6, 7, §11-3 #6,
12.
|
|
|
F 3/2/012
|
HW due: Read §11-6 (note: skip §11-4 and §11-5); write §11-6 #3, 8.
|
|
|
M 3/5/012
|
HW due: Write §11-6 #10, p. 593 #R6ab.
|
|
|
T 3/6/012
|
HW due: Read §12-1; write the work showing the long
division of 6/(1 – x); write §12-1 #1-7 all.
|
|
|
W 3/7/012
|
Test (100
pts.) on §9-8, §9-9, §9-10, and all of Chapter 10.
|
|
|
Th
3/8/012
|
No additional HW due. Get some good sleep.
|
|
|
F 3/9/012
|
HW due: Read §12-2 and §12-3; write §12-2 #7abcde,
8abc, §12-3 #1-11 as many as time permits.
In class: Guest speaker from the NRC, Ms. Suzanne Schroer. Ms. Schroer is a
nuclear engineer and a graduate of the University of Missouri at Rolla.
Please bring some good questions for her!
|
|
|
M 3/12/012
|
No additional HW due today. Tuesday’s assignment
will be posted by 3 p.m. today (Monday).
In class: Engineering video. You will love it, guaranteed.
|
|
|
T 3/13/012
|
HW due:
1. Finish §12-3 #1-11 all.
2. Read §§12-4 and 12-5.
3. Mark up your book as indicated below.
Mark-ups to your book:
1. On p. 615, heavily underline or circle the word could in the
statement of #6c. It is important for you to understand that simply because
the terms approach zero, that is no guarantee that
the series must converge. The classic counterexample is the harmonic series, 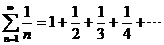 , ,
which diverges by comparison with the divergent improper integral 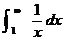 . .
2. On p. 616, the preamble should say “expansion about x = a” (typo).
3. Another typo: Near the middle of p. 623, change the equation 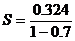 to to
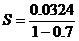 . .
4. On p. 636, near the middle of the page, change the 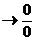 notation to notation to 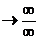 . .
5. On p. 651, in #R6b, insert the word “of” between “interval” and
“convergence.”
6. On p. 651, in #R6c, change the phrase “Write the fifth five terms” to
“Write the first five terms.”
7. Finally, if you have not already done so, mark all the intervals of
convergence for the “Eight Well-Known Power Series” on p. 616: 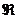 for the first five,
then (0, 2] for the ln x series, (−1, 1) for the
geometric series, and [−1, 1] for the arctan x series. Sometime before spring break,
we will have a memory quiz on the eight series and their intervals of
convergence. for the first five,
then (0, 2] for the ln x series, (−1, 1) for the
geometric series, and [−1, 1] for the arctan x series. Sometime before spring break,
we will have a memory quiz on the eight series and their intervals of
convergence.
|
|
|
W 3/14/012
|
HW due: Memorize all 8 of the power series and their
intervals of convergence on p. 616. In celebration of Pi Day and the first
truly warm day of the year, there is no additional written HW due.
|
|
|
Th
3/15/012
|
HW due: Write §12-4 #6abc, 7.
Quiz will test your memorization
of the 8 power series on p. 616 and their convergence intervals. A second,
easier quiz on recent terminology is also possible.
|
|
|
F 3/16/012
|
HW due: Read §12-6; write §12-5 #9, 12, 14, 15,
21-25 all, 29, §12-6 #1-6 all.
Note: Insert the word “open” before
the word “interval” in the instructions for §12-6 #1b-6b. The second problem
is worked for you as an example.
2(a). 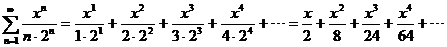
(b) 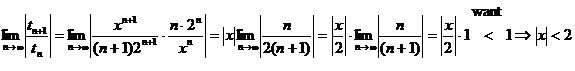
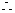 open interval of cgce. is (–2, 2) open interval of cgce. is (–2, 2)
(c) radius of cgce. = 2
|
|
|
M 3/19/012
|
HW due:
1. Make the following typographic corrections to your textbook:
(a) On p. 627, #14, place an xn in the numerator
of the summand.
(b) On p. 633, change the variable in the limit expression,
lim (ln b – ln 6),
to be b instead of n.
(c) On p. 636, add the 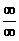 expression to the
second application of L’Hôpital’s rule, to match
the first. expression to the
second application of L’Hôpital’s rule, to match
the first.
2. Read §12-7 and the green boxes on p. 630.
3. Write §12-6 #14, 22, 23, 25.
4. Compute the coefficient of the x4
term in the Maclaurin series expansion of sec2
x. Do this in 2 different ways:
(a) (The hard way.) Long-divide 1 by the Maclaurin series for cos x to get a series for sec x. Show your work, and check your
answer on wolframalpha.com. Then multiply that series for sec x by itself, collecting terms to see
what the coefficient on x4
will be.
(b) (The easy way.) Take the Maclaurin
series for tan x from your Friday class
notes (or copied from wolframalpha.com). Do something clever to that series,
term by term, to find a series for sec2 x, and look at the x4
term to get your answer.
5. Find the first 4 terms in the Maclaurin series
expansion for 2 ln |sec x|. Please be clever. (Note:
This is one that wolframalpha.com won’t give you. If you are clever, you can
get this in about 30 seconds. Feel free to use facts from #4 to help you.)
|
|
|
T 3/20/012
|
HW due:
1. For #5 from yesterday’s set (the Maclaurin
expansion for 2 ln |sec x|), write a grammatically correct sentence to explain how one
should correctly handle the “+ C”
from the term-by-term antidifferention of the tan x series.
2. Write §12-7 #5, 6, 8, 10.
|
|
|
W 3/21/012
|
HW due:
1. Explain (one sentence) why it is not possible to find a Maclaurin series expansion for f (x) = x–1.
2.(a, b) Find a Taylor series expansion for f (x)
= x–1 by using 2
different methods. Be creative! Try to use methods that take less than a
minute each, if possible.
(c) Determine the interval of convergence for the series
you found in parts (a) and (b).
3. Write §12-7 #7, 9, 11-14 all, 19, 25-30. Note: Problems 25-30 are to be done by inspection. Simply give a
short reason for each.
|
|
|
|
Spring break, March 22–April 1.
|
|