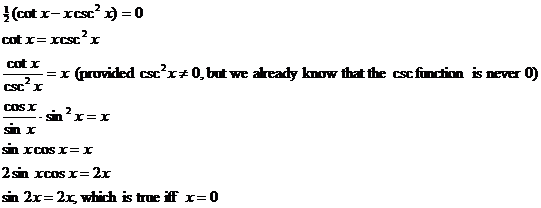|
Th
12/1/011
|
HW due: Read §8-3; write §8-2 #15, 16, 18, 24, 40.
|
|
|
F 12/2/011
|
HW due: Read §8-4; write §8-3 #5, 12, 21, and one
other of your choice.
|
|
|
M 12/5/011
|
HW due:
1. Important: Change your class notes from last Friday to reflect the
typographical corrections below.
2. Read §8-5.
3. Write §8-3 #17, 18, 22.
4. Write §8-4 #1-4 all.
Corrections
For §8-3 #5, the domain for x
should have been written as 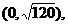 not not 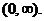 Bonus point goes to Pryce and Lane (half
point each) for pointing this out after the end of class. Also, Pryce and
Lane each pick up another half point for spotting a discrepancy between
“min.” and “max.” in the solution. Jonathan’s solution included the equation Bonus point goes to Pryce and Lane (half
point each) for pointing this out after the end of class. Also, Pryce and
Lane each pick up another half point for spotting a discrepancy between
“min.” and “max.” in the solution. Jonathan’s solution included the equation 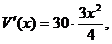 which he set equal to 0. However, there was a typo in this
equation. He meant to write which he set equal to 0. However, there was a typo in this
equation. He meant to write 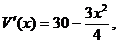 which would give which would give 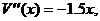 which means that which means that 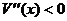 whenever x > 0. whenever x > 0.
Therefore, the conclusion should be that the critical point at 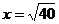 gives a local maximum, and since there are no other
critical points and no endpoints to check, the local max. is
a global max. as well. That writeup
needs to be part of a full-credit solution. gives a local maximum, and since there are no other
critical points and no endpoints to check, the local max. is
a global max. as well. That writeup
needs to be part of a full-credit solution.
For §8-3 #21, the endpoint at 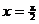 does need to be
checked. The objective function is the area function, A(x), and we need to
compute and show does need to be
checked. The objective function is the area function, A(x), and we need to
compute and show 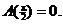
One other error that went unnoticed in #21 is that the algebraic evaluation
of the derivative was overly complicated. From the equation in which the
derivative, 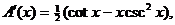 was set equal to 0,
we should have written was set equal to 0,
we should have written
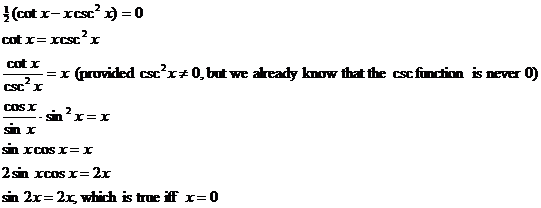
By root finder, x = 0 is the only
solution, but that solution is not in the domain 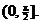 Therefore, the
objective function has no critical points. The area value when Therefore, the
objective function has no critical points. The area value when 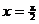 is 0, but the
maximum area value of 0.5 is not attained on the domain. Answer: No
maximum. is 0, but the
maximum area value of 0.5 is not attained on the domain. Answer: No
maximum.
|
|
|
T 12/6/011
|
St. Nicholas Day. If you leave a shoe overnight in
the classroom on Monday night, you may receive some candy in it today.
HW due: Write §8-4 #5, 11, 14, 19, 20, 24.
In class: DBO #1 (Director of Bakery Operations) will help us understand
volume calculations by plane slicing.
|
|
|
W 12/7/011
|
Pearl Harbor Day.
HW due: Write §8-5 #2, 13, 14. A sketch is required for each problem.
In class: DBO #2 will help us to understand volume calculations by
cylindrical shells and radial slicing.
|
|
|
Th
12/8/011
|
HW due: Read §8-6; write §8-6 #1, 2, 3.
|
|
|
F 12/9/011
|
HW due: Read §8-7; write §8-6 #17, 18, 22, and the
two problems below.
Proof 1: Prove that the area under
any parabolic arch equals 
Proof 2: A paraboloid of revolution is the solid formed when a parabolic arch is
revolved about its axis of symmetry. Use the result of the first proof to
prove a general formula for the volume of a paraboloid
of revolution.
|
|
|
M 12/12/011
|
HW due: Do the review problems listed below. If you cannot
finish them all for today, do as many as you can, and finish the rest by
Tuesday.
1. Use the method of plane slicing
with planes parallel to the axis of a paraboloid of
revolution to prove that the volume is 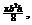 where b = diameter of base, h = height. where b = diameter of base, h = height.
2. For the diff. eq. 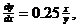 answer questions
32-34 on p. 349. answer questions
32-34 on p. 349.
3. Redo #34 for x = 10.5 and a step
size of 0.1. Is your estimate for y
more accurate now?
4. Write the general solution equation for the logistic diff. eq. dP/dt = kP(A – P).
5. In #4, what does A signify?
6. In #4, what value of t produces
the maximum value of dP/dt? (Give a
general description.)
7. Write #R3, R4, R5, and R6 on pp. 428-429.
8. Write definitions of inflection
point, local minimum, local maximum, plateau point, and critical point.
In class: Review for test.
|
|
|
T 12/13/011
|
HW due:
1. At the very end of #R6c(iii), after class time had run out, I hurriedly
wrote the limits of integration for the dy integral (cylindrical
shells) as 1 to 5. However, since the integral is a dy integral, and y clearly varies between 0 and 4, the
limits of integration are 0 to 4. Please make this correction to your notes.
(Both integrals will then yield the same answer.)
2. Finish your review problems.
Note that our test has been moved to Wednesday, since there is apparently no
AP Bio test conflicting with our test after all.
|
|
|
W 12/14/011
|
Test (100
pts.) on all recent material, especially volumes of solids of revolution and
volume of arbitrary solids by plane slicing.
Arc length (§8-7) will not be on this test. Work problems 4 and 5 from February 2009
if you desire some additional good practice. The answer is 157.193 cubic
units.
It is a good bet that there will be at least one proof on the test. You can practice
by using the calculus to prove that the area of any triangle equals bh/2. When
setting up your diagram, make sure that the diagram is “wlog”
and that your base and height are clearly labeled.
|
|
|
Th
12/15/011
|
HW due: No additional written work is due. However,
your review problems may be collected, and various other problems from
earlier in the semester may be spot-checked.
A general homework amnesty and clearing out of notebooks will occur at the
end of the first semester.
|
|
|
F 12/16/011
|
HW due: Write §8-7 #2, 14, 22. This set is shorter
than usual because of the dress rehearsal for chorale students. If you have
extra time, go ahead and read §8-9. Note:
We are skipping §8-8.
|
|
|
M 12/19/011
|
HW due: Read §8-9 if you have not already done so.
|
|
|
T 12/20/011
|
HW due: Write §8-9 #1-4 all, 6, 13, 14, 18,
20abcdef.
Note: For #20b, you have to set up
and solve what is called an integral
equation (not a diff. eq., an “int. eq.”). The upper endpoint of the
integration is unknown, but you can call the unknown upper endpoint X and
feed the integral into your calculator’s root finder. The answer turns out to
be approximately 1.88976005 radians. You are supposed to be able to do this,
but if you can’t, then simply show the setup in your problem writeup and ask someone to show you how to solve for the
upper endpoint in class.
In class: Review.
|
|
|
W 12/21/011
|
Big Quiz (60 pts.) on standard and polar arc length,
plus a question on optimization (min/max), plus a few questions on
definitions (critical point, plateau point, cusp, point of inflection, etc.). If you are absent today for a planned reason, you
must take a make-up version of the Big Quiz in advance.
|
|