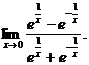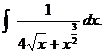|
T 11/1/011
|
HW due:
1. Read §§6-4 and 6-5.
2. Write §6-4 #12, §6-5 #3-24 mo3, and the proof of CRI, the Chain Rule for
Integrals (below).
CRI: Under suitable conditions, 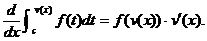
|
|
|
W 11/2/011
|
HW due: Read §6-6; write
§6-6 #6-12 even, 20, 21.
|
|
|
Th
11/3/011
|
HW due: Read §6-7; write
§6-7 #3-54 mo3.
|
|
|
F 11/4/011
|
No school (faculty meetings).
|
|
|
M 11/7/011
|
HW due: Read §§6-8 and 6-9; write §6-8 #3-36 mo3 and
the two problems below. Note that for several of these, you will have to use
the “limit of the log” technique demonstrated in Example 3 on p. 287. We did
not have time to cover this technique in class, but it is straightforward
enough that you should (hopefully) be able to read it and learn it on your
own.
38. Evaluate 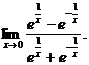
39. Evaluate 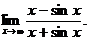
|
|
|
T 11/8/011
|
HW due: Read §7-2; write §6-9 #1-90 all, or at least
as many as you can do in one evening. Be sure to allow part of your time to work
on problems #81-90, regardless of whether or not you do all of #1-80.
|
|
|
W 11/9/011
|
HW due: Finish §6-9 #1-90 all; also write §7-1 #5, 6
(Note: converses of each other),
§7-2 #2.
|
|
|
Th
11/10/011
|
HW due: Read §7-3; write §7-2 #5, §7-3 #3. Note: In #5b, it is permissible to use
the shortcut that all exponential growth or decay problems have a solution of
the form y = Pert, where P
= initial amount present, and r (or
k, if you prefer) is a constant
determined by the initial conditions. You should have learned this fact in precalculus.
|
|
|
F 11/11/011
|
HW due: Read §7-4 (review of material previously
discussed in class); write §7-3 #10, §7-4 #2, 4.
|
|
|
M 11/14/011
|
HW due: Write p. 301 #C6, p. 302 #T6-T18 all, pp.
341-342 #R1-R3d all, R4abc. You should be able to do all of these, except
possibly for #C6, which is a joke. (Hint:
#C6 works out better if you change the problem so that the integrand is
divided by ln 10.)
Keep a time log. Any of these problems that you are not able to complete over
the weekend should be on your study list in preparation for tomorrow’s test.
|
|
|
T 11/15/011
|
Test (100
pts.) on all recent material, through §7-4. Important: Bring your HW review problems
with you so that they can be graded during the test. It is expected that by
now you will have completed the entire set of problems. The solution to the modified joke problem, #C6, is
below.
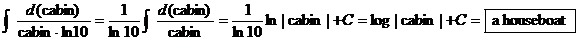
Or, you can leave the problem in its original form, as follows:

Ha ha. Ha.
|
|
|
W 11/16/011
|
HW due:
1. Read §7-5.
2. Compute 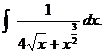 Hint: Let u = Hint: Let u = 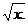 Show work. Show work.
|
|
|
Th
11/17/011
|
No class (Cathedral service during A period).
|
|
|
F 11/18/011
|
Oops! Today’s assignment was supposed to be posted
by 3 p.m. Thursday, but because of a house furnace failure (thermostat,
actually), your Fearless Teacher was distracted and forgot to post it in
time. Thus there is no additional HW due today.
|
|
|
M 11/21/011
|
HW due:
1. If you have not already created the EULER1 program, do it now:
:ClrHome
:Disp "DIFFEQ MUST BE"
:Disp "IN Y1."
:Prompt H
:Prompt X
:Prompt Y
:Lbl AA
:Y+Y1H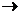 Y Y
:X+H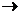 X X
:Disp "NEW X="
:Disp X
:Disp "NEW Y="
:Disp Y
:Disp "PRESS ENTER"
:Pause
:Goto AA
[Press 2nd QUIT to get out of the programming mode.]
2. Write §7-5 #3, with the following adjustments:
For #3(b), do the first 4 lines in the table (i = 0, 1, 2, and 3) by hand,
showing all steps. For 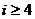 , i.e., for , i.e., for 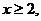 simply rely on your calculator program and fill in the
values for x = 2, 3, 4, 5, 6, and
7. Important:
Use the table format given in class, complete with accurate column headings. Column
headings should be as follows: simply rely on your calculator program and fill in the
values for x = 2, 3, 4, 5, 6, and
7. Important:
Use the table format given in class, complete with accurate column headings. Column
headings should be as follows:
i xi yi 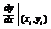 dy = dy = 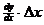 new y = yi
+ 1 = yi
+ dy new y = yi
+ 1 = yi
+ dy
For #3(c), there is no need to make a photocopy. Simply make a large sketch
of Figure 7-5c in your notes (including the exact solution), and add your
values from the table. This is good practice for you. Large size is required,
so that the differences between the solution tracks can be seen clearly.
For #3(d), make your plot for step size = 0.1 on the same set of axes that
you used before. Label the curves so that there is no confusion.
|
|
|
T 11/22/011
|
HW due: Write §7-5 #7, 8. Note: We started with the diff. eq. 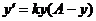 in class. Note that
the k in the equation of the
solution (top of p. 338) is not the same k
as the one in the diff. eq. we wrote in class. in class. Note that
the k in the equation of the
solution (top of p. 338) is not the same k
as the one in the diff. eq. we wrote in class.
In the STAtistics class, we would insist that your
answer to #7c included a residual-plot analysis. However, since this is only
a HappyCal class, it is acceptable to compare your
fits based on the value of the r2
variable. When comparing r2
values, larger is better. If your r2
value is not displayed, use 2nd CATALOG DiagnosticOn
and try again.
Specific instructions (in case you have forgotten how to perform
regressions): Store your P values
in list L1, your 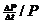 values in list L2,
and use STAT CALC 8 L1,L2 ENTER (or STAT CALC 9, STAT
CALC 0, or STAT CALC ALPHA A) to perform the regression. values in list L2,
and use STAT CALC 8 L1,L2 ENTER (or STAT CALC 9, STAT
CALC 0, or STAT CALC ALPHA A) to perform the regression.
|
|
|
W 11/23/011
|
No school (Thanksgiving break).
|
|
|
M 11/28/011
|
School resumes.
In class: Review of logistic growth.
|
|
|
T 11/29/011
|
HW due:
1. If you have not already done so, finish the problems assigned last week.
Make sure that your answer to #8c is in the form P(t) = A/(1 + Ce–Akt),
where A = carrying capacity
(determined by algebra), C = a
constant determined by initial conditions, and k = the proportionality constant given when the diff. eq. dP/dt = kP(A – P) is constructed by algebraically transforming the result of
#7d.
2. Memorize the equation P(t) = A/(1 + Ce–Akt) and the
purpose of A and k. That is what you need to know for
the AP exam.
3. Write §7-6 #6, 13, 15. Use your Euler’s Method program to compute a
sequence of ordered pairs in each case. The trickiest question is the second
part of #6 (how to tell whether to start going to the right or to the left),
and you may find the following hint helpful: The diff. eq. in #5 on p. 340
actually gives dF/dt as the
numerator and dR/dt as the
denominator. By the parametric chain rule, their quotient is dF/dR as shown.
|
|
|
W 11/30/011
|
HW due:
1. Prove that the solution P(t) = A/(1 + Ce–Akt)
satisfies the diff. eq. dP/dt
= kP(A – P). Note: This is much easier than deriving the solution
when starting from the diff. eq., which we have already done. Simply show
that the solution we obtained actually works. (This is analogous to checking
the answer to an indefinite integral problem by taking the derivative and
making sure that you obtain the integrand.)
2. Show that different values of C
in the equation P(t) = A/(1 + Ce–Akt)
create different members of a family of similarly shaped ogive
curves. (Plug in and plot the curve for several different values of C, where A and k are held fixed.) Label the values of C that you use. Choose ugly, random decimal values of C.
3. Let k = 0.0003 be fixed. Find
the value of C such that P(0) = A/10. Prove that for this value of C, the maximum rate of increase occurs
when P = 0.5A. Assume that A is a positive parameter, but leave A
as a letter, not as a specified numeric value.
4. How do you propose generalizing and remembering the fact that you
discovered in #3?
5. Read §8-2. Reading notes are required, as always.
6. Write §8-2 #13, 14.
|
|