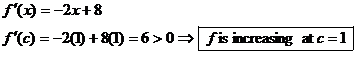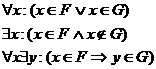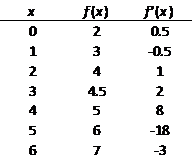|
W 9/7/011
|
First day of school.
|
|
|
Th
9/8/011
|
HW due:
1. Send Mr. Hansen a signed e-mail from the address you check most
frequently. See contact information.
2. Watch the Greek letter video.
3. Watch the Roman letter video.
4. Optional: Watch the Hippasus video. This will eventually be required, so
if you have extra time tonight, go ahead and watch it.
In class:
Given: No dog has 17 legs.
Given: Every normal (uninjured) dog has 4 more legs than
no dog.
Conclusion: Every normal dog has 21 legs.
Meta-conclusion (a conclusion about the conclusion):
We must be careful to avoid using the
expression “no dog” to mean two different things.
Given: A(k) = “A man
with k hairs on his head is almost
bald.”
Given: A(1) is true.
Given: Adding just 1 hair to an almost-bald man does not
change his baldness status.
Conclusion: By mathematical induction, 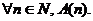 In English: Every
man is almost bald. In English: Every
man is almost bald.
Meta-conclusion:
______________________________________________
|
|
|
F 9/9/011
|
HW due:
1. If you have not already done so, watch the Hippasus video.
2. If necessary, review the steps for mathematical induction: If A(1) is true,
and if 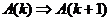 for any natural
number k, then proposition A(n)
must be true for any natural number n. for any natural
number k, then proposition A(n)
must be true for any natural number n.
3. Prove, by mathematical induction, that the sum of the first n odd natural numbers equals n2. Be clear.
4. Find the flaw in the second exercise from yesterday. Write your answer as
a meta-conclusion. Be clear, and use complete sentences.
5. Be prepared for a possible quiz over anything discussed so far.
|
|
|
M 9/12/011
|
HW due:
1. Correct Friday’s induction proof. Do not copy the version below, but you
may use it for inspiration. Be sure that your proof ends with “Q.E.D.” or the
Halmos sign.
Theorem: 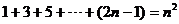
Proof: Let P(k) denote the proposition that 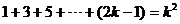 , i.e., that the sum of the first k odd natural numbers equals k2.
Since P(1)
is the claim that 1 = 12, which is clearly true, the basis case is
established. , i.e., that the sum of the first k odd natural numbers equals k2.
Since P(1)
is the claim that 1 = 12, which is clearly true, the basis case is
established.
It remains only to show that 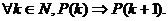 If P(k), as defined above, is true, we can add
the next odd number, namely (2k +
1), to each side to get If P(k), as defined above, is true, we can add
the next odd number, namely (2k +
1), to each side to get 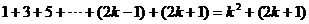 . By algebra, 2k
+ 1 can be rewritten as 2(k + 1) –
1, and k2 + (2k + 1) can be rewritten as (k + 1)2. Therefore, we have . By algebra, 2k
+ 1 can be rewritten as 2(k + 1) –
1, and k2 + (2k + 1) can be rewritten as (k + 1)2. Therefore, we have
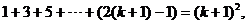 which is precisely
proposition P(k + 1). Since the truth of P(k) forced P(k + 1) to be true,
the induction step is satisified. which is precisely
proposition P(k + 1). Since the truth of P(k) forced P(k + 1) to be true,
the induction step is satisified.
Conclusion: P(n) is true for any natural number n. 
2. Write as many of the following problems as you can, using the formatting
style specified in the HW guidelines. The first one is done for you.
§1-2 #16c. f (x) = –x2 + 8x + 5,
c = 1
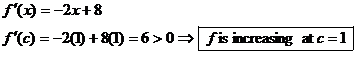
Rate of increase
= slope of tangent line = 6.
§1-2 #20c.
§1-3 #12-14 all.
§1-5 #16.
§2-3 #24.
|
|
|
T 9/13/011
|
HW due:
1. Finish yesterday’s assignment if you have not already done so. Make sure
that each problem conforms to the “formula, plug-ins, work with explanation,
circled answer with units” template for clear and consistent presentation.
2. Prepare §2-4 #1-20 all for oral presentation only. Don’t be caught
flat-footed!
3. Write a nontechnical definition of continuity in your own words. However,
you may not use the “baby”
definition given in precalculus and earlier courses
of a continuous function as being one whose graph can be drawn without
lifting one’s pencil.
4. Let L be a real number, and let f be a function whose domain is  . In your own words, write a correct definition of the
limit L of a function f (x)
as . In your own words, write a correct definition of the
limit L of a function f (x)
as  . Try to use as few symbols as possible. . Try to use as few symbols as possible.
5. Write §2-4 #59-66 all.
|
|
|
W 9/14/011
|
HW due:
1. Write §3-3 #11.
2. Use your calculator’s MATH 8 feature (numeric derivative at a point) to
compute the derivative of the absolute value function (a) at x = –2, (b) at x = 3, and (c) at x =
0. For part (d), explain why your calculator gives the wrong answer for (c).
What should the correct answer be? Note:
The syntax of the MATH 8 feature is nDeriv(function,wrt,value) ENTER, where “function” is the
function of interest, “wrt” is the “with respect
to” variable, usually x, and
“value” is the value at which the derivative is to be evaluated.
3. Negate each of the following:
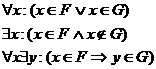
|
|
|
Th
9/15/011
|
HW due:
1. The truth table for the “implies” operation 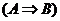 is defined as
follows: is defined as
follows:
A B A
implies B
______________________
1 1 1
1 0 0
0 1 1
0 0 1
(Note: This is a form of the
Boolean calculus in which 0=false, 1=true. An implication is defined to be
true in all cases except where the hypothesis is true and the conclusion is
false. The Boolean calculus is named for George Boole, the first
mathematician to make a thorough formal system for logic.)
Prove that this is the same truth table that we get by evaluating 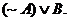 (In your writeup, show columns for A, ~A, and B, as well as the final result column.) (In your writeup, show columns for A, ~A, and B, as well as the final result column.)
2. Write the negation of the standard 2-sided symbolic limit definition for a
limit L of function f (x)
as x approaches c.
3. Write the symbolic definition of what it would mean in order to have 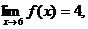 where function f is defined as follows: where function f is defined as follows:
f (x) = (x – 3)2 – 5 for 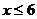
f (x) = 4.00001 for x > 6.
Note: The limit does not equal 4.
That is not the question. The question is to write what would be true if the limit were equal to 4.
4. Use the negated limit definition to prove that the limit of function f (x)
as x approaches 6, in the previous
question, does not equal 4.
5. State the values of 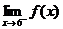 and and
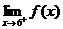 , i.e., the 1-sided limits. , i.e., the 1-sided limits.
6. We already know that a 2-sided limit exists if and only if both 1-sided
limits exist and are equal. However, use the negated definition, not the
inequality of the 1-sided limits, to prove that function f from the previous three questions does not have a limit as x approaches 6. Hint: Consider cases. If you did #4, you have already shown that
the limit cannot equal 4. It suffices to show that no number less than 4 can
be the limit, nor can any number between 4 and 4.00001 be the limit, nor can
any number greater than or equal to 4.00001 be the limit.
|
|
|
F 9/16/011
|
HW due:
1. Take some time to get caught up on previously assigned HW. If you need to
call a friend (or Mr. Hansen) for hints, please do so.
2. Reread and review §3-4. (Reading notes are required, as always. You will
probably not be reminded in the future.)
3. Prepare §3-4 #1-12 for oral presentation. Practice reading the answer in
the proper notation. For example, you would read the answer for #5 as “M prime of x equals 0” or “dM/dx
equals 0.”
4. Write §3-4 #14-22 even, plus 30 and 38.
|
|
|
M 9/19/011
|
HW due:
1. Write §3-5 #7.
2. Read §3-7.
3. Write §3-7 #2-22 even (NB: If
stuck, do the preceding odd problem and check answer in back of book).
4. Write §3-7 #25.
|
|
|
T 9/20/011
|
HW due:
1. Review the green box on p. 114. This is a review of information you should
have learned in precal. It will probably not be retaught, but if necessary, we can do a couple of examples
in class during our review.
2. Write §3-8 #1, 2.
3. Write §3-9 #2-24 even. Problems 11 and 23 are solved for you below as
examples.
11.
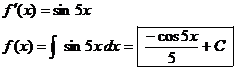
23.
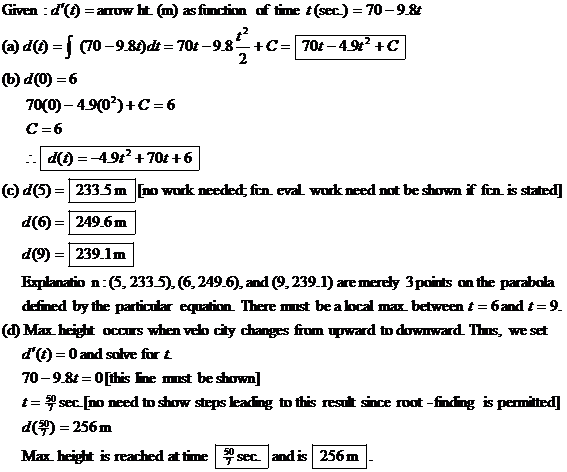
In class: Review of Chapters 1, 2, and 3, including §3-9. If time permits, we
may also look at this practice test
from 2008. The material emphasized varies somewhat from one year to the
next, but you should be able to answer virtually all of the questions on that
practice test. The practice tests at the end of each chapter in your textbook
are also good for practicing!
|
|
|
W 9/21/011
|
Test on Chapters 1, 2, and 3 (100 points).
Note: Test will be held in MH-001
and will start at 8:00 sharp. Extended-time students should arrive at 7:30
for setup and an early start.
|
|
|
Th
9/22/011
|
HW due: Sleep and/or get
caught up on previously assigned problems. No additional work is due.
|
|
|
F 9/23/011
|
HW due: Sleep and come in
early at 7:45 a.m. to watch the video on fractals that we were going to watch
yesterday. Seniors will be on retreat today.
The video has a running time of 54 minutes and will start at 7:46 sharp. If
you arrive late, please sneak in quietly without disturbing us. Your arrival
time will be noted.
Note: Seniors and others who cannot
make it in by 7:45 will be expected to make up the missed portion of the
video next week.
|
|
|
M 9/26/011
|
HW due: Correct last week’s test until it is 100% correct. It
is better if you write out a fresh set of answers on a blank copy of the
test, but if your corrections are minimal, it is acceptable to mark them
(using a different color of ink) on the test itself. If you did not already
pick up your test, it will be e-mailed to you over the weekend.
|
|
|
T 9/27/011
|
HW due: Read §§4-2 and 4-3.
Reading notes are required, as always.
|
|
|
W 9/28/011
|
Form VI: Please report to class at 7:45 to watch the
first half of last week’s video.
All other forms: Please slip in quietly at 8:00, or come early if you would
like to see more of the video (nothing wrong with that!). Seeing things a second time is a good way to learn,
even if it is slightly boring.
HW due: Read §4-4; write §4-2 #8, 12, 20, 23, 24, 29; write §4-3 #2, 16, 24.
|
|
|
Th
9/29/011
|
Form VI: Please report to class at 7:45 to watch the
second half of last week’s video.
All other forms: Please slip in quietly at 8:00, or come early if you would
like to see more of the video (nothing wrong with that!). Seeing things a second time is a good way to learn,
even if it is slightly [see how you could fill in that word without even
thinking?].
HW due: Read §4-5; write §4-4 #3-36 mo3, 41, 43. Also, find a third example
of a function that is its own derivative. We saw two examples yesterday in
class: the function y = ex and the function y = 0.
|
|
|
F 9/30/011
|
HW due: Read §4-6; write
§4-5 #5, 15-24 mo3, and the 2 extra problems below.
Extra problem 1: We have now seen
3 functions that have the property of equaling their own derivative, namely y = ex, y = 0,
and y = –ex. We also discussed how any “left shift” or “right
shift” of these functions would also work. (As you learned in precal, a replacement of x by x – h shifts a graph h units to the right.) Your task is to summarize all these
infinitely many solutions by using a single equation having a single
parameter.
Extra problem 2: Read the green
box on p. 153. Use the formula found there, or another method if you prefer,
to find 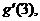 given that given that 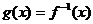 and given that
function f is an invertible
function satisfying the following table: and given that
function f is an invertible
function satisfying the following table:
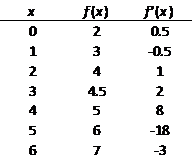
|
|