|
T 3/1/011
|
HW due: As described in
class. For people who missed class, or perhaps did not hear all of the
details, some information is furnished below.
Group 1: Nick R.-S., Justin, Dominique
Group 2: Alex, Andrew, Phineas
Group 3: Daniel, Chick, Preston
Group 4: Jamie, Julien, Brennan
Group 5: Edward, Zeke, Jordan
Group 6: Nick S., Tip, Andrei, Ousmane
Group leaders (underlined above) are required to submit an experiment
proposal, approximately one page handwritten or half a page typed. A hard
copy is required. As always, if the group leader is absent for any reason, he
must deputize someone else in the group to bring the required hard copy
submission to class.
1. State your research question.
2. Write your proposed methodology. Human subjects are not required, but if
you use human subjects, you must provide a consent form. All proposals will
be reviewed and discussed before being approved. Mr. Hansen will serve as
your IRB. If you use blinding (good) or double blinding (even better), be
sure to specify how you will execute the logistical details.
3. Specify the statistical test(s) you intend to use (1-prop. z, 2-sample t, 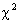 g.o.f., etc.). g.o.f., etc.).
4. Predict the result you think you may see (the “effect size”).
5. Estimate the sample size you will need in order to demonstrate statistical
significance. Do not worry about calculating this accurately; we will discuss
how to do this in class.
An example is provided below.
1. Does Axe brand body spray change the acceptability of STA Third Formers to
NCS 9th graders?
2. A panel of volunteer NCS freshmen will sit on the second tier of a set of
bleachers. One by one, volunteer STA Third Formers will walk past,
approaching within about 18 inches of each NCS panelist. After passing all of
them, the STA student will turn around once at a designated mark on the
floor, flash a thumbs-up sign, make eye contact with the panel, and then walk
past them a second time and exit. Nothing shall be said. STA students will be
sent at equally spaced intervals, and half of them (randomly determined) will
have been spritzed with a measured amount of Axe brand body spray immediately
before their strut. Panelists shall rate each STA volunteer on a Likert scale
of 0 to 10 for each of 3 categories: neatness, athletic condition, and
overall attractiveness.
3. Three 2-sample t tests will be
used in order to compare the mean ratings of the control and treatment STA
students for each of the categories: neatness, athletic condition, and
overall attractiveness.
4. We predict that the ratings for athletic condition will show no
statistically significant difference. We predict that the mean scores for
neatness and overall attractiveness will be lower for the Axe-wearing
students, with a mean effect size of −1.5 points on the Likert scale
used.
5. A panel of 5 NCS students and 24 STA volunteers should be large enough to
establish the predicted outcomes.
|
|
|
W 3/2/011
|
HW due: Answer the Group 2
power problem below. Then log your points.
Group 2 (Alex, Phineas, and Andrew) proposed yesterday to give quizzes
to 2 groups of 17 volunteers, randomly divided into treatment and control.
The treatment group will be informed in advance of the format and nature of
the quiz, while the control group will take the quiz “cold” in a room in
Marriott Hall. Scores will be computed based on time, with penalty time
assessed for wrong answers. Alex and his group believe that the effect size
(abbreviation: ES) that they will see will be a mean difference of about 2
seconds faster for the treatment group. For both groups, s = 6 seconds is a reasonable estimate of the s.d. of the scores.
In class, we decided that a 2-sample t
test would be appropriate for testing the hypotheses
H0: True means are equal
Ha: Treatment group has
a smaller mean.
Sketch the sampling distribution of the difference of means, subject to the H0 assumption. Then,
determine (a) the probability of Type I error if 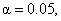 and (b) the
probability of rejecting H0
if the true ES (not the ES that will necessarily be seen, but the true ES) is 2 seconds. and (b) the
probability of rejecting H0
if the true ES (not the ES that will necessarily be seen, but the true ES) is 2 seconds.
Probability (b) is called power and
equals 1 minus the probability of Type II error. Sketches and supporting work
are required.
Student question submitted by e-mail:
I really have no idea how to figure out what the [Type II] error value is,
especially given that we do not actually have any data. Could you point me in the right direction?
Answer:
If you have sketched the sampling distribution of the difference of sample
means, you should have a bell-shaped (or actually t-shaped) curve centered on 0, with s.e. = 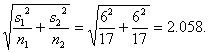
I presume you can sketch that. The s.e. formula comes from #2 in the tan box
on p. 585.
If 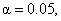 we will reject H0 whenever the t statistic (based on control mean
minus treatment mean) exceeds 1.7. (Where does the 1.7 come from? Look at the
t* table at the very last back
cover page of your textbook. With df = 32, which is what your
calculator tells you when you run a 2-sample t test, you need to look in the .90 column, since that column
gives you a right-tail area of 0.05. The t*
value from the table is 1.7.) we will reject H0 whenever the t statistic (based on control mean
minus treatment mean) exceeds 1.7. (Where does the 1.7 come from? Look at the
t* table at the very last back
cover page of your textbook. With df = 32, which is what your
calculator tells you when you run a 2-sample t test, you need to look in the .90 column, since that column
gives you a right-tail area of 0.05. The t*
value from the table is 1.7.)
OK, so now we know that whenever the t
statistic is 1.7 or greater, we will reject H0. Since the s.e. is 2.058 seconds, a t* value of 1.7 means that we have to
be (1.7)(2.058) = 3.4986 seconds above zero for our difference of sample
means before our 2-sample t test
will tell us that we have achieved statistical significance.
Remember that number: 3.4986. The question is, if the true ES, the true
difference of sample means, equals 2 seconds, then how often will we achieve
a difference of 3.4986 seconds or greater? Remember, that’s the goal, since
if we do not surpass 3.4986, then we will not have enough evidence to reject H0.
I won’t do the whole problem for you, but at this point you are almost
finished. You can use algebra to figure out how far (in t units) 3.4986 is above 2, and then you can use tcdf on your
calculator to figure out the area under the curve to the right of whatever
that answer was. The tcdf function gives you the answer to part (b), which we
call power (statistical power of the test). If you want the
probability of Type II error, which was not requested, you would subtract the
power from 1.
|
|
|
Th 3/3/011
|
HW due: Read the
supplementary material below; finish yesterday’s assignment; answer the
problem below. Then log your points.
Supplementary reading:
Remember that the t statistic tells
you the direction (positive or negative) of the ES, in standard error units. This is exactly the same as the
situation we saw with the z test
statistic, and going back as far as last fall, with the z score for univariate data.
Remember, if your teacher tells you that you scored z = −0.75 on a test whose mean was 78 and whose s.d. was 8,
what does that mean? It means that you were three-quarters of a standard
deviation unit below the mean. Since three-fourths of 8 is 6, your raw score
must have been 72.
In a similar way, yesterday’s problem involved a t* score of 1.7. That value can be converted to seconds by
multiplying by the s.e., namely 2.058, and adding the center value of the t distribution, namely 0. The result,
in seconds, is 3.4986, and it is 3.4986 seconds that marks the “big fat red boundary
line” that separates rejecting H0
from failing to reject H0.
To convert from seconds back into t
units, simply apply the process in reverse: t = (difference in seconds)/s.e.
Supplementary problem:
(c) Show that the power of the test, the answer to yesterday’s part (b), is
0.236. Note that df = 32 (thanks to Daniel K. for the typo correction!).
(d) Compute the probability of Type II error, assuming that the true ES is 2
seconds.
(e) Explain why the power would more than triple if the true ES were 5
seconds. A carefully drawn sketch will suffice. Computations are welcome but
are not required.
(f) Would the probability of Type II error increase or decrease if the true
ES were increased from 2 seconds to 5 seconds? Explain briefly (no work
required).
(g) The standard notation for the probability of Type I error is 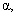 and the standard
notation for the probability of Type II error is and the standard
notation for the probability of Type II error is 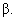 Explain why neither
power nor Explain why neither
power nor 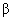 can be computed at
all unless we first specify a particular instance of Ha, i.e., a particular value for the ES. can be computed at
all unless we first specify a particular instance of Ha, i.e., a particular value for the ES.
(h) Assume that Group 2 has re-thought the problem and has decided that the
true ES is probably closer to 4 seconds. Also assume that Mr. Hansen has
re-estimated the value of s to be 5
seconds. Now, compute the power of the test if Group 2 is willing to use 26
volunteers in each group, instead of 17. Is the power acceptable now? What do
you think? Hint: Since df = 50 now,
you can safely average the t*
entries for df = 40 and df = 60 in order to obtain the
new t* value.
|
|
|
F 3/4/011
|
HW due: Answer the problem
below and revisit parts (e) through (h) of yesterday’s problem. It is
presumed, at this point, that you already have completely correct, clear,
legible answers to parts (a) through (d). Log your points based on the
quality of (e) through (k).
Supplementary problem:
Carefully sketch a bell-shaped sampling distribution for a statistic in a two-tailed significance test, and show
the big fat red lines that mark the boundaries of the “reject H0” regions. Label all
three regions appropriately. Then, use very thin tissue paper (or, if you
prefer, a piece of clear plastic) to show an alternative sampling
distribution of the same size and shape. Move your alternative distribution
(your “Ousmane,” so to speak) left and right in order to answer the following
questions. Bring your sketch and your overlay to class.
(i) If everything else stays the same, but the center point of the
alternative distribution is shifted from +4 units to +6 units, what happens
to power and 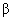 ? Do they increase or decrease? ? Do they increase or decrease?
(j) If everything else stays the same, but the center point of the
alternative distribution is shifted from +4 units to −4 units, what
happens to power and 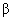 ? Do they increase or decrease? ? Do they increase or decrease?
(k) If everything else stays the same, but the 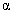 value is increased,
what happens to power and value is increased,
what happens to power and 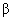 ? Do they increase or decrease? ? Do they increase or decrease?
|
|
|
M 3/7/011
|
No additional HW due. This
is your chance to get some sleep and/or catch up on older assignments.
However, please read the material below if you would like to correct your
notes from Friday.
Note: Last Friday, in the notes
written on the board, the sample wording was presented in this format: “The
power of the test is _____ against the _____ alternative.” The first blank is
obviously a number, expressed either as a decimal or as a percentage. As for
the second blank, students requested some sample content, and your fearless
instructor provided the following:
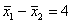
Well, guess what? That cannot possibly be correct, since hypotheses (both
null and alternative) must always refer to parameters, not to statistics. Therefore, the second blank could be
filled in with something like the following:
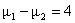
or
true ES = 4.
Here are some examples of correct ways to word statements involving
statistical power:
1. The power of the 2-sample t test
in this situation is 88% against an effect size of 4 units.
2. The power of the 2-sample t test
is 0.88 against the alternative hypothesis that 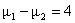 . .
3. The power of the 1-prop. z test
(with H0: p = 0.38) is 0.65 against the
alternative that p = 0.32.
4. The power of the LSRL t test
(with H0: 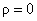 ) is 99.3% against the ) is 99.3% against the 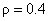 alternative. alternative.
|
|
|
T 3/8/011
|
HW due: Read pp. 695-697
(omitting green box on p. 695), tan box on p. 704, middle of p. 706 to bottom
of p. 707. Instead of the tan box at the top of p. 707, read the simplified assumptions for the LSRL t test on our STAT TESTS handout.
Then, write the problem below and log your points.
Problem:
(l) Carefully sketch plausible sampling distributions related to H0 and Ha in some imaginary problem involving a one-tailed t or z test for which 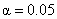 . Label the “reject H0”
and “fail to reject H0”
zones clearly, and show the boundary between them as a thick line. If you
have a second color of pencil (or a colored pen) that you can use for the
boundary line and the Ha
sampling distribution, so much the better. Position the Ha sampling distribution in such a way that the power (i.e.,
the portion in the “reject” zone) is 30%. . Label the “reject H0”
and “fail to reject H0”
zones clearly, and show the boundary between them as a thick line. If you
have a second color of pencil (or a colored pen) that you can use for the
boundary line and the Ha
sampling distribution, so much the better. Position the Ha sampling distribution in such a way that the power (i.e.,
the portion in the “reject” zone) is 30%.
Question: If the sample size quadruples while all other aspects of the
problem stay the same, what happens to the power? Estimate a numeric value
for your answer—but do not attempt
to use formulas to compute an answer unless you are a real glutton for
punishment. A second sketch is required. Score your work based on neatness.
Big hints:
1. All of our s.e. formulas involve n
(or some variation of n1
and n2) in the square
root of a denominator. Therefore, a quadrupling of sample size will result in
a halving of s.e., since 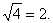 Both distributions
in the second sketch must therefore be taller and narrower. Both distributions
in the second sketch must therefore be taller and narrower.
2. The big fat red line will have to move as a result of hint #1. This is to
be expected. Simply adjust the position of the big fat red line, in the
second sketch, so that 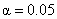 is kept constant. is kept constant.
3. Leave ES unchanged in the second sketch. Remember, ES tells you the center
of the Ha sampling
distribution.
|
|
|
W 3/9/011
|
HW due: Write #13.1, 13.4acd,
13.62ab. Then log your points. Remember, if you claim 4 points,
you are pledging not only that you made a solid effort for 35 or more minutes
on the night of the assignment, but also that you will correct the work fully
based on any later classroom discussion.
For #13.62a, the answer is not “yes” or “no”; you need to run a PHA(S)TPC
test using
H0: 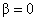
Ha: 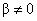
Also, note that there is a typo in the regression equation, which should be 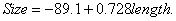
For #13.62b, the hypotheses become
H0: 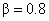
Ha: 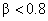
For both #13.62a and #13.62b, you will need to refer to the raw data on p.
236 in order to check assumptions. You may use either the book’s list on p.
707 or the simplified list on our
STAT TESTS handout.
If you choose the simplified approach, you would check assumptions 1-3 as
follows:
1. Say, “The LSRL is a good fit, so that the mean y value for each x
value lies on the LSRL.” A reasonably high value of r2 (anything more than about 0.3) and a residual plot
devoid of patterns or outliers will suffice. Be sure to show a sketch of the
residual plot, and state the r or r2 value.
2. Assert that the variability of the residuals does not depend on x. This conclusion is supported if the
residual plot does not show any “flange” outward (as in Figure 13.15(c) on p.
717) for especially large or small values of x. Write, “The residual plot shows that the variability of
residuals does not seem to change as x
changes.”
3. Assert that the residuals are normally distributed about the LSRL. Again,
this is impossible to check thoroughly, but if the NQP of the residuals is
reasonably straight, the assertion is reasonable. You will need to show a
histogram or an NQP of the residuals as documentation.
If you choose the book’s approach, you would write out 4 assumptions and
would deal with them as follows:
1. Assert that the true residuals (what your book calls error values, e) are centered about the LSRL. There
is no way to prove this, but if the residual plot (which you will have to
sketch) shows no patterns, this is a plausible claim. Remember, we do not
know what the e values are; all we
know are the sampled residual values, which may or may not have the same
distribution as the true e values.
2. Same as #2 in the simplified list (see above).
3. Same as #3 in the simplified list (see above).
4. Assert that the true residuals (e
values) are independent. There is no convenient way to check or prove this,
and this assumption is frequently violated in practice.
For #13.62a, use your calculator’s STAT TESTS LinRegTTest feature after
entering the data in L1 and L2. For #13.62b, you will
have to calculate a new t value,
since you cannot use the 15.26 in the table on p. 742. Hint: The t value you
will use, again with df = 9, is −1.485, but you need to show your work.
The computation of t = −1.485
is easy (a single step, simple algebra), but you need to show it.
|
|
|
Th 3/10/011
|
HW due: Finish #13.62b
based on the large extra hint given in class; write #13.64abcdef. In part
(f), use 95% for your confidence level. Then, log your points and take Mr. Hansen’s AP poll.
|
|
|
F 3/11/011
|
HW due: Prepare for our review day by writing at
least one item that is both (a) a question for which you care to know the
answer and (b) a question, or a fragment of a question, that could
legitimately be asked on Monday’s test. Then, log your points.
If you wish to write more than one, that is fine, too.
IMPORTANT: More than half the
class also still needs to take Mr.
Hansen’s AP poll. If you do not answer the poll, there will be a small
point penalty, and Mr. Hansen will hound you mercilessly over the weekend.
Example review question (good):
Use sketches to show that if all other aspects of a 2-tailed statistical test
remain unchanged, then an attempt to reduce the probability of Type I error
will always reduce the test’s power.
Example review question (mediocre):
A LSRL t-test involves 37 data
points (i.e., 37 ordered pairs). Compute df.
Example review question (mediocre):
A 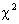 test for independence
involves two categorical variables, one with 5 different values (VG, G, A, P,
VP) and one with 3 different values (red, blue, green). Compute df. test for independence
involves two categorical variables, one with 5 different values (VG, G, A, P,
VP) and one with 3 different values (red, blue, green). Compute df.
Example review question (poor):
What name is given to the quantity 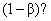
In class: Review for Monday’s test. We will go through as many of your
questions as time permits.
|
|
|
M 3/14/011
|
Test on
Chapters 12 and 13 (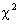 tests, LSRL t-tests, and power), 100 points. As announced in class last Friday, your writeup of
#13.64abcdef will be collected before the test starts. The assignment will be
graded for correctness, neatness, and completeness (4 points for each).
Neatness need not be excessive, but legibility and proper notation are
required. There is no need to log the points, because this assignment will be
collected from each student. If the only way you can get the correct set of
answers is by copying Mr. Hansen’s work (posted on hwstore.org), then that is what you will
have to do. Copying is not the best way to learn, but it is a possible way to
learn, provided you pay attention to what you are writing. tests, LSRL t-tests, and power), 100 points. As announced in class last Friday, your writeup of
#13.64abcdef will be collected before the test starts. The assignment will be
graded for correctness, neatness, and completeness (4 points for each).
Neatness need not be excessive, but legibility and proper notation are
required. There is no need to log the points, because this assignment will be
collected from each student. If the only way you can get the correct set of
answers is by copying Mr. Hansen’s work (posted on hwstore.org), then that is what you will
have to do. Copying is not the best way to learn, but it is a possible way to
learn, provided you pay attention to what you are writing.
There are 103 points on the test, but the test will be scored out of 100.
Thus there are 3 bonus points built-in, plus a fourth bonus point if you
remember your spare batteries. Format of the test is as follows:
Part I: Definitions (8 terms, 1.5
points each, 12 points total)
You will be provided with 8 terms and a list of 14 possible definitions. On
the list of 14 possible definitions, 8 are correct and 6 are phony. Your task
is to write a correct definition for each of the 8 given terms. Note: You will not be allowed to do
the matching by using letters or drawing lines. You must rewrite the
definition exactly as presented in the list of 14 choices. Suggested time,
since the answers are provided and need not be fully retrieved from “deep
memory,” is 4 minutes, 6 minutes for extended timers.
Part II: Power Sketching (8 points)
You will be given a scenario involving either a one-tailed or a two-tailed t or z test, with specified values for 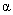 , s.e., and ES. You will be asked to estimate by how much
the power will increase or decrease when some aspect of the test changes. Two
reasonably neat sketches are required, with two sampling distributions for
each. Suggested time is 4 minutes, 6 minutes for extended timers. , s.e., and ES. You will be asked to estimate by how much
the power will increase or decrease when some aspect of the test changes. Two
reasonably neat sketches are required, with two sampling distributions for
each. Suggested time is 4 minutes, 6 minutes for extended timers.
Part III: Calculation of an Expected
Count in a 2-Way 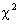 Test (6 points) Test (6 points)
You will be given a 2-way table and told to calculate the expected count at a
certain position. Work is required. For example, if the table is a 3 x 5
table (3 rows, 5 columns), and you are asked to find the expected count at
row 2, column 1, you would proceed as follows:
Original 2-way table: 
Grand total is 281.
Row 2 total is 62.
Column 1 total is 41.
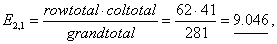
which is easily verified by running STAT TESTS and checking the “expected”
matrix. Note that this matrix also satisfies one of the assumptions for a
2-way 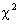 test, namely that
all expected counts are at least 5. (If necessary, you can relax the
assumption and say that all expected counts are at least 1, and no more than
20% of the expected counts are less than 5, but the “all expected counts are
at least 5” assumption is OK and is certainly easy to check.) test, namely that
all expected counts are at least 5. (If necessary, you can relax the
assumption and say that all expected counts are at least 1, and no more than
20% of the expected counts are less than 5, but the “all expected counts are
at least 5” assumption is OK and is certainly easy to check.)
Suggested time is 3 minutes, 4.5 minutes for extended timers.
Part IV: 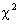 Tests (two
statistical tests, one scored 3,3,6,3,3,6 for PHA(S)TPC, the other
0,3,6,3,3,6) Tests (two
statistical tests, one scored 3,3,6,3,3,6 for PHA(S)TPC, the other
0,3,6,3,3,6)
One of the tests will be a g.o.f. test, and one of the tests will be a 2-way
test for independence or homogeneity of proportions. The tests will not be
identified. Extended timers will do only one of these, but the choice will
not be announced until the test is given, and the problem type will not be
identified. Suggested time is 13 minutes for each test, or 26 minutes total
for regular timers (same as AP standard).
Note: Calculation of expected
counts need not be shown, since that skill was already tested in Part III.
Just let your calculator do the work when finding expected counts. The only
work you are expected to show is the calculation of the first two (2) terms
of the 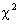 statistic. statistic.
There is no need to define parameters for a 2-way 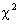 test (independence
or homogeneity of proportions), since that would be unacceptably tedious,
especially for a large 2-way table. test (independence
or homogeneity of proportions), since that would be unacceptably tedious,
especially for a large 2-way table.
Here is an example of a g.o.f. problem, with full writeup and work:
Problem: George claims that the
M&M’s in his store have a distribution pattern of 15% for red, orange,
yellow, and green, 20% for blue, and 20% for brown. His business partner,
Georgette, pulls an SRS of 1000 candies and finds 15.1% red, 17.2% orange,
13.7% yellow, 14.2% green, 20.1% blue, and 19.7% brown. Is there evidence
against what George has claimed? Use 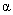 = 0.05. = 0.05.
Solution:
Let pred,
porange, etc. = true proportions
of red, orange, etc.
H0:
pred = .15, porange = .15, pyellow = .15, pgreen
= .15, pblue = .20, pbrown = .20
Ha:
At least one proportion is not as claimed.
Assumptions for 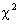 g.o.f. test: g.o.f. test:
SRS? Yes, given.
[All data converted to
counts?  easily done by multiplying by n = 1000] easily done by multiplying by n = 1000]
All exp. counts 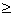 5? Yes, they are
150, 150, 150, 150, 200, 200, resp. 5? Yes, they are
150, 150, 150, 150, 200, 200, resp. 
Test statistic: 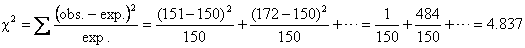
P = 0.436
with df = 5
Concl.: There is no evidence (n = 1000, 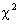 = 4.837, df = 5, P > 0.4) against George’s claims
regarding the true distribution of M&M colors. = 4.837, df = 5, P > 0.4) against George’s claims
regarding the true distribution of M&M colors.
Part V: LSRL t Test (3,3,6,3,3,6 for PHA(S)TPC, 8 points for additional
questions)
This problem will be similar to #13.62 or #13.64 in the textbook. Note that
you may be required to deduce the value of 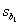 based on information
in a computer-style printout or based on information disguised elsewhere in
the problem. based on information
in a computer-style printout or based on information disguised elsewhere in
the problem.
You may also be required to calculate a C.I. for the LSRL slope, b1, and you may be asked to
interpret the LSRL slope in the context of the problem. Interpretation must
follow this template: “For each additional 1 unit of __________ , the model
predicts an increase [or decrease] of __________ units of __________ .”
Suggested time is 13 minutes (same as AP standard).
Total time is 50 minutes, or 55.5 minutes for extended timers. Extended
timers should plan on staying a few minutes late. Tardiness excuses to the
next class will be provided for extended timers but not for regular timers.
|
|
|
T 3/15/011
|
HW due: Pick up the pieces on yesterday’s test, as
described below. Your #13.64abcdef will also be collected. Do not log the
points, since both assignments will be collected. Record your elapsed time
for each problem. If you work with classmates, you must list their names.
Working with classmates or tutors is permitted only if the written work on
the page is your own work (not copied). Copying of someone else’s work would
be an honor violation, except for #13.64, for which I stated earlier that you
could copy from the version posted at hwstore.org
if you had to.
The timings on the test were fairly accurate, but only for people who had
practiced and kept moving relentlessly forward. Only a few students submitted
papers that were essentially complete. Almost everyone omitted most or all of
#13 from the test. Therefore, I
expect everyone to redo the entire problem #13, beginning to end,
except for Andrew, who needs only to use a correct value of 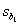 in part (c) when
computing the confidence interval. in part (c) when
computing the confidence interval.
People who were sick on the day of the test also need to do #13 from the test, since it is quite
similar to #13.64abcdef from the homework and will make a good review for the
make-up test.
Alex, Chick, Daniel, Tip, Nick S., Jordan, Dominique, Edward, and the extra-timers
all need to redo #12 from the test as
part of their homework due today.
Phineas, Alex, Jordan, Preston, and Andrei all need to redo #10 and #11 from the test as part
of their homework due today.
Finally, in the interest of fairness, anyone else who wishes to redo #10 and #11 or #12 may submit a version for “enhanced consideration.”
|
|
|
W 3/16/011
|
HW due: Finish your “patching up” from the test if
you have not already done so. Starting today, start bringing your Barron’s AP
review book to class instead of your course textbook.
|
|
|
Th 3/17/011
|
HW due: Prepare for a 2-question quiz based on the Must-Pass Quiz. You will be given 2
questions, a starred one and a non-starred one, both selected at random. If
you miss any portion of the starred question, your score is 0. If you get the
starred one correct, your score will be somewhere between 5 and 10.
Handwritten notes will be permitted for today’s quiz. However, when you take
the MPQ for real, in May, no notes are allowed.
In class: There are still 3 students who need to select their spring break
book to read. After all reading assignments are settled, we will finish going
over the AP formula sheet, which is found near the end of your Barron’s
review book. Be sure to bring the Barron’s book with you!
Chick is on the tote board with 44 (0.5 pt.), 2 (1 pt.), and 53 (0.6 pt.),
1.1 mulligans remaining. If he fails, there will be no penalty.
|
|
|
F 3/18/011
|
No additional HW due. However, a general HW check is
likely. If you take a cut today or are absent for any reason, you will need
to call Mr. Hansen over spring break and read randomly requested problems.
(Or, scan and fax.)
|
|
|
|
Spring break.
|
|