|
M 1/3/011
|
Classes resume. No
additional written HW is due. However, you should definitely set aside
several days during the week of Dec. 20-24, and several more during the week of
Dec. 27-31, to review for your midterm exam. Questions on the midterm will be
drawn largely from the Barron’s AP Statistics review book, topics 1-12.
AP Statistics has four themes:
1. Exploratory Data Analysis
2. Planning a Study
3. Probability (including random variables and sampling distributions)
4. Statistical Inference
Of these four themes, you are responsible for the first three for your midterm exam. However, in Theme Two
(“Planning a Study”), questions will not be quite as in-depth as those shown
in the review book, since we have not yet had the experience of running an
experiment as a group project with blocking and comparison of treatments.
However, all the terminology in Theme Two should be familiar to you and can
be tested. Here is a partial list of terminology from Theme Two: bias,
sampling error, control group, placebo, blinding, confounding, experimental
units, control/randomization/replication, blocking, realism.
All assigned reading from the textbook is fair game. Check over the HW archives
for September through December if you have any questions about what reading
assignments have been made. Virtually the entire textbook through Chapter 8
is included on the midterm exam, with the exception of the material on
logistic regression (pp. 255-262) and Bayes’ Theorem (pp. 330-332).
Important: Do not make the mistake
of thinking that if you can answer all the questions on all previous tests,
then you are prepared for the midterm exam. Because of time limitations, not
all topics could be tested during in-class tests. For example, you are
responsible for the facts given in the tan boxes on pp. 380-381, even though
there were no quiz or test questions that specifically featured them. The
Barron’s book has numerous sample questions on these facts (see topic 10,
“Combining Independent Random Variables”). Also, on the 2004 test, you can see that the
tan boxes on pp. 380-381 are employed in questions 3 and 4.
If you wish, we can of course do some additional examples in class during the
week of Jan. 3. Please make a list of specific questions you would like to
see addressed.
Another example of a skill for which you are responsible but which has not
yet appeared on tests is the design and execution of probability simulations
(Monte Carlo method). An example problem is given below. If you send your
solution by e-mail, I will critique it and will tell you how many points you
would have earned.
Simulation Example:
If a fair coin is flipped 10 times, what is the probability that at least one
run of 5 heads in a row (HHHHH) or at least one run of 5 tails in a row
(TTTTT) occurs somewhere in the sequence of 10 flips? To address this
question, you must
(a) design a simulation procedure employing the random digit table on pp.
814-815 of your textbook, and
(b) estimate the requested probability by computing 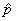 over the course of
15 simulated iterations of your procedure. over the course of
15 simulated iterations of your procedure.
Part (a) is worth 5 points, allocated as follows:
1 point for describing what digit(s) correspond
to “heads” and what digit(s) correspond to “tails”
1 point for describing what constitutes one
iteration of your simulation (be sure to indicate starting row #)
1 point for describing what constitutes
“success” and “failure,” and how you will tabulate the results
1 point for describing what you will do in
order to compute 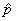
1 point for correctly describing what 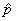 signifies (no credit
if, for example, you say signifies (no credit
if, for example, you say 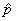 = the probability) = the probability)
Part (b) is worth 3 points, allocated as follows:
1 point for making a clear tabulation that
shows exactly how 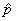 was computed was computed
1 point for correctly computing 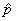 from your data from your data
1 point for correctly labeling your answer as 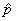 or “sample
proportion” or “sample
proportion”
There are no half points. Any point that is not fully awarded is scored as 0.
Total scores would then translate to an AP scale approximately as follows:
0 or 1 point = failure = F = AP “1”
2 points = failure = D = AP “2”
3 or 4 points = low pass = C = AP “3”
5 or 6 points = pass = B = AP “4”
7 or 8 points = high pass = A = AP “5”
|
|
|
T 1/4/011
|
HW due: Answer the
questions below. Show enough work (using proper notation) so that it is clear
that you know what you are talking about.
1. Shaquille O’Neal has a career free throw average of 52.7% and once missed
11 free throws in a single game. Imagine a player with similar
characteristics and a free throw probability of success given by p = 0.527, independent of what has
happened on other attempts. If such a player has 12 free throw attempts in a
game, compute the probability that he sinks at least one free throw. Show a
little work.
2. The reason Mr. Hansen wrote the word “SCREENING” in all capital letters is
that all of that information about the probability of disease given a
positive reading on a screening test applies only to SCREENING TESTS (i.e.,
tests performed on members of the general public who have no disease
symptoms). Explain why the probability of having a disease might be very
different if the person taking the test is showing some symptoms that
correlate with the disease in question.
3. A would-be terrorist has concocted a new, relatively harmless disease
called applephobia that sometimes causes people to drop their iPhones without
warning. There are no other symptoms, and even the iPhone dropping is not a
reliable indicator, since it happens only slightly more frequently than it
would happen with uninfected people. There is now an inexpensive blood test
for applephobia that gives a negative reading in 95% of people who truly do
not have applephobia and a positive reading in 94% of people who truly do
have applephobia. The incidence of applephobia in the general population is
approximately 0.5%, based on careful statistical study using much more
expensive tests.
(a) State the sensitivity, the specificity, the probability of Type I error,
and the probability of Type II error for the inexpensive blood test. Identify
each number clearly. If you wish, you may use the standard symbols 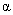 (alpha) for P(Type I error) and (alpha) for P(Type I error) and 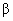 (beta) for P(Type II error). (beta) for P(Type II error).
(b) Use a tree diagram to compute P(applephobia
| positive reading). This number is called the positive predictive value (PPV) of the screening test.
(c) Explain why PPV declines if the specificity
declines. [Note: The boldface
words correct a typo in the original version of this question. Everyone in
the class has been awarded a typo point.]
(d) PPV can be increased either by raising the sensitivity or by raising the
specificity. Which is more beneficial: a small improvement in sensitivity, or
a small improvement in specificity? Why?
(e) In the real world, sensitivity and specificity almost always are in a
tradeoff situation. In other words, increasing the sensitivity causes the
specificity to decrease, and increasing the specificity causes the
sensitivity to decrease. Screening applies in many non-medical fields, and
one common example is e-mail. Explain how increasing the sensitivity of a
spam-detection program (i.e., reducing 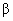 ) would almost certainly cause a reduction in specificity
(i.e., an increase in ) would almost certainly cause a reduction in specificity
(i.e., an increase in 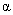 ). ).
|
|
|
W 1/5/011
|
HW due: Answer #3(c) from
yesterday’s assignment (note correction), plus the questions below.
1. What are the four themes of AP Statistics?
2. If a fair coin is flipped 10 times, what is the probability that at least
one run of 5 heads in a row (HHHHH) or at least one run of 5 tails in a row
(TTTTT) occurs somewhere in the sequence of 10 flips? To address this
question, you must
(a) design a simulation procedure employing the random digit table on pp.
814-815 of your textbook, and
(b) estimate the requested probability by computing 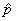 over the course of
15 simulated iterations of your procedure. over the course of
15 simulated iterations of your procedure.
3. Score your work in #2 by using the scoring guide in the 1/3/011 calendar
entry. Show your point assessment for part (a), part (b), and the total.
Circle the total.
|
|
|
Th 1/6/011
|
HW due:
1. Answer #3(c) from the 1/4/011 assignment (note typo correction). This problem
was previously assigned, but some people forgot to do it for yesterday.
2. Re-do all of the Dec. 16 test on Chapter 8.
Try to answer all questions perfectly correctly. If you use someone else’s
wording (including Mr. Hansen’s wording, or the wording from your textbook),
you must acknowledge in writing that
the words are not your own. For this assignment, that is acceptable.
(Normally, acknowledging that the words are not your own would save you from
having to face the Honor Council, but you would not earn any points.)
3. [Optional.] Use this scoring guide to
estimate your score on the Dec. 16 test. As before, there will be a small
2-point bonus if your estimate is within 5 points of the score you actually
earned.
In class: Review.
|
|
|
F 1/7/011
|
Last day of quarter; no
additional written HW due.
In class: Review.
There are still 13 students who need to do the “Excelcise” skill test, which
counts for 20 points pass/fail. For details, please see calendar entry for
10/28/010.
|
|
|
M 1/10/011
|
Mr. Hansen will be on
campus (primarily MH-102) from approximately 8:30 a.m. until 3:00 p.m. today,
with a lunch break at 1:00.
Any Mathcross puzzles that you wish
to submit for extra credit must be received by 3:00 p.m. today. It is best to
hand them to Mr. Hansen in person, or you can use e-mail if you prefer. (If
you use e-mail, please send a screen shot of your completed puzzle. Use the
SHIFT+PrintSc key to store the screen image into the copy buffer; then paste
the image into Paintbrush or PowerPoint. Save the screen shot as a file, and
then attach that file to your e-mail.)
Because there were some people absent last Friday for unavoidable reasons,
the deadline for your “Excelcise” 20-point task has also been extended until
3:00 p.m. today.
|
|
|
W 1/12/011
|
Midterm Exam, 11:00 a.m.−1:00 p.m., Steuart
201-202. Questions will be drawn
largely from the Barron’s review book, with some numbers altered to
discourage straight memorization. You are not responsible for any of the
questions on Theme 4, Inferential Statistics, but essentially everything else
is fair game.
So far, we have studied Themes 1 through 3: Exploratory Data Analysis,
Planning a Study (including blocking and matched pairs), and Probability
(including random variables, simulations, and sampling distributions).
There are a number of topics that we covered in class but did not have time
to include fully on quizzes and tests. Some areas in which your previous
tests and quizzes have given you insufficient numbers of questions include
the following:
- Calculating mean and standard deviation for multiples or linear
combinations of random variables
- Interpreting 2-way tables
- Finding the missing entry in a 2-way table in order to ensure
independence (hint: assume equal
proportions)
- Interpreting cumulative density graphs as opposed to simple
density graphs
- Interpreting LSRL slope and intercept in the context of the
problem
- Nonlinear curve fitting
- Type I and Type II errors, PPV, and tree diagrams (covered in
class and homework, but not tested yet)
- Explaining the purpose of blocking (namely, to reduce the variability among
experimental units, so that the experimental effect, if any, can be more
readily seen).
There are a total of 160 points possible on the exam. Actual grade cutoffs
will be determined after all scores are in, but you can use the following as
an approximate guide:
128-160 points = AP 5 = A
104-127 points = AP 4 = B
80-103 points = AP 3 = C
56-79 points = AP 2 = D
0-55 points = AP 1 = F
The exam will last 96 minutes, ending at about 12:40 p.m. Format of the exam
will be as follows:
Part I: Multiple Choice, 45 minutes,
80 points
20 questions, 4 points each, 2.25 minutes per question on
average
There is no partial credit in this section, but beginning this
year, there is no penalty for wrong guesses.
In bygone years, an “A” would consist of approximately 15 correct
answers, 2 wrong answers, and 3
omitted answers. However, since you can now guess without
penalty, the “A” threshold will now require
approximately 16 correct answers out of 20. The rationale is that
if you can answer 15 correctly through
course knowledge alone, then the expected value (mean) of the
other 5 that you can guess will be 1.
Part II: Free Response, 51 minutes, 80
points
3 questions, 2 short (approximately 13 minutes each) and 1
long (approximately 25 minutes)
Short problems are worth 20 points each, and the long problem is
worth 40 points. Scoring will use the
“holistic” AP approach, in which each portion is scored on a 0-4
scale that corresponds closely to an AP
grade of 1 through 5, or a letter scale of F through A. Each
“holistic” point is then multiplied by 5 (or 10 in
the case of the long problem) in order to obtain a point score.
Although AP graders never use half points
in the holistic grading, Mr. Hansen sometimes uses half points to
resolve borderline situations.
Approximate guide to interpreting holistic scores:
0 = AP 1 “clueless”
1 = AP 2 “developing”
2 = AP 3 “low pass”
3 = AP 4 “pass”
4 = AP 5 “high pass”
For example, if you score 2 on each of the short problems in Part
II and 3 on the long problem, your
weighted average would be 10 + 10 + 30 = 50 out of 80. If you
also had 14 correct answers (i.e.,
56 points) in Part I, that would give you a total score of 106
out of 160 (66.25%), which is a B (AP 4).
Total length of exam will be 96 minutes, but you cannot start Part II until
the time for Part I has expired. Do not worry if you cannot finish all
questions in the time provided; that is quite typical. Most students find
that they finish Part I with time to spare but do very poorly on Part I.
Then, on Part II, they run out of time but do fairly well on Part II. Thus,
the part that seems easy is actually super-hard, and the part that seems hard
(because you are likely to run out of time) is actually reasonable. By taking
some practice tests with the Barron’s book, you can determine your own
characteristics. Allow 2.25 minutes for each multiple-choice problem, plus 13
or 25 minutes for each free-response problem, depending on whether it is a
“short” or a “long.”
Perfection in Part II is not required in order to earn a holistic “4” score.
Minor rounding errors and the like are typically overlooked. However, you
must use correct notation throughout, and you must justify any use of normal
(z) curves to approximate the
sampling distribution of 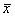 or or 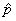 . Remember, in the case of the sampling distribution of . Remember, in the case of the sampling distribution of 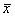 , we look for finite s.d. and n , we look for finite s.d. and n 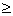 30, and we apply
CLT. In the case of the sampling distribution of 30, and we apply
CLT. In the case of the sampling distribution of 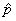 , we check whether all 3 rules of thumb are satisfied; if
so, we can proceed with a normal approximation, but if not, we will have no
choice except to use the binomial distribution. , we check whether all 3 rules of thumb are satisfied; if
so, we can proceed with a normal approximation, but if not, we will have no
choice except to use the binomial distribution.
Extended-time students will have 67.5 minutes for Part I and 76.5 minutes for
Part II, for a total examination time of slightly under 2.5 hours. In order
to qualify for extended time, a student must have a certification on file
with Dr. Viola. Extended timers who wish to start Part II at the 45-minute
break may do so, but otherwise they must wait out the full 67.5 minutes
before beginning Part II.
|
|
|
W 1/19/011
|
Classes resume.
In class: We launch Theme IV, Inferential Statistics, after reviewing the
others.
|
|
|
Th 1/20/011
|
HW due: Read pp. 475-480,
482-488; write #9.2.
|
|
|
F 1/21/011
|
HW due: Reread p. 487,
especially the italicized passages; read pp. 488-492, 495-500; write #9.16.
|
|
|
M 1/24/011
|
HW due: Read pp. 500-505;
write #9.30 and the exercise below.
Exercise: Let “R” and “D” denote clusters
of Republicans and Democrats, respectively. Suppose we have a state with 4
congressional districts and equal populations of Republicans and Democrats,
as shown in the diagram below. Democrats are concentrated in the cities, and
Republicans have a majority in the less densely populated portions of the
state. Copy the diagram 3 times, and draw district boundaries in such a way
that
(a) each party will probably win 2 districts
(b) the Republicans will probably win 3 of the 4 districts
(c) the Democrats will probably win 3 of the 4 districts

Finally, write
(d) a short paragraph about what you have learned about representative
democracy. Are the wishes of the voting population necessarily reflected in
the makeup of Congress? What statistical topic is illustrated here?
|
|
|
T 1/25/011
|
HW due: Read pp. 508-513;
write #9.53, 9.61, 9.62.
|
|
|
W 1/26/011
|
HW due: Read pp. 525-529
and the top half of p. 531; write #10.1, 10.2, 10.3, 10.4.
|
|
|
Th 1/27/011
|
Snow day (no school). The
assignment that was originally due today will be due tomorrow (Friday)
instead.
If you have trouble doing the assignment, you are expected to “phone a
friend,” consult the Internet, or call Mr. Hansen at 703-599-6624. Mr. Hansen
will not be going anywhere until Thursday evening at the earliest.
|
|
|
F 1/28/011
|
HW due: Read pp. 531-534;
write #10.12, 10.15, 10.17, 10.21.
In class: Review.
Answers to these questions are as follows:
10.12
(a) False positive = Type I error.
(b) Type I: We reject the null hypothesis (the hypothesis of no cancer) in
favor of an alternative claiming that cancer is present. Therefore, we subject
the patient to extreme stress as well as costly and painful tests, biopsies,
and/or exploratory surgery. If the probability of Type I error is high, the
cost (across the entire health-care system) might literally be greater than
the benefit of searching for cancer in the first place. In other words, since
some people will always die of cancer anyway, it might be the case that
allowing those deaths to occur without intervention is the best use of public
resources. Obviously, decisions like this are fraught with political baggage.
(“Death panels,” anyone?) However, unless the money to spend on medical care
is infinite, decisions have to be made at some point.
(c) Type II: We fail to reject the null hypothesis (the hypothesis of no
cancer) even though the patient has cancer. The consequences are either (1)
the patient dies sooner than s/he otherwise would have, owing to the lack of
treatment, or (2) the patient experiences no adverse consequences because
something else causes death first, or (3) the patient experiences no adverse
consequences because the cancer is of a type that is slow-growing and
essentially harmless. Believe it or not, situation (3) is actually quite
common with certain types of cancers. Many of the women treated for breast
cancer, for example, have what is called “carcinoma in situ,” which is not
dangerous at all, and they would have literally been better off if they had
never been diagnosed in the first place.
(d) There is an inherent tradeoff between Type I and Type II errors. As long
as all other aspects of the testing environment remain fixed (sample size,
incidence, etc.), the decision to be more careful in testing (so as to reduce
the risk of Type I error, false positives) will increase the risk of Type II
error (undetected cancers). There is no free lunch!
10.15
(a) Pizza Hut’s conclusion is a rejection of H0.
(b) To reject H0
erroneously is, by definition, a Type I error.
10.17
Answers in back of book (p. 843) are good.
10.21
Answers in back of book (p. 843) are good.
|
|
|
M 1/31/011
|
Test (100 pts.) through §10.2.
|
|
