|
W 12/1/001
|
HW due: Write pp. 413-415
#7.70, 7.72, 7.73, 7.76, 7.79.
In class: Guest speaker (Mr. Joe Morris of MITRE Corporation) and review for
test.
|
|
|
Th 12/2/010
|
Quiz on this
week’s “Quick Study” article,
but no additional written HW is due. Previously assigned problems may be
scanned a second time. Problems covered in class or on handouts must be 100%
corrected in order to qualify for credit.
In class: Additional review and test preparation.
|
|
|
F 12/3/010
|
Test (100 pts.) on Chapter 7 (through p. 416 only).
NOTE: Test will begin at 9:25 sharp
for extended timers, 9:45 for everyone else. Because of the Christmas House
Tour, there is no assembly period today.
Since we did not get to the Quick Study quiz yesterday, that quiz will be
postponed until Monday.
As you know, I feel strongly that college-bound students should know how to
study and should know how to prepare their own practice tests for themselves.
Teachers who make things really easy for you at every step and tell you
essentially what will be on the test are wonderful, in a sense, but you will
seldom have things that way in college. (And, cough cough, AP Statistics is a
college-level course.) However, in response to overwhelming demand from
students, I am posting a practice test from 2005
and an answer key. Some of the recent HW
solutions are also posted on hwstore.org.
|
|
|
M 12/6/010
|
HW due: Visit hwstore.org, and correct (until they are 100%
correct) your HW problems that were due on Nov. 30 and Dec. 1. Please use a
different color of pencil or pen for your corrections. The margins are the
preferred location for making corrections (as shown on the HW guidelines). However, for these two assignments,
if you did not leave adequate space in the margins, you may put your
corrections below the original problems, as long as they are clearly marked.
Also, we will have our quiz on last
week’s “Quick Study” article today.
|
|
|
T 12/7/010
|
HW due: Prepare for your
Excelcise task, and practice until you can perform all the steps within the
5-minute time limit. If you have forgotten the steps, they are listed under
the HW archives for 10/28.
Here are some useful shortcuts to remember:
1. Select in direction of cursor movement: SHIFT + arrow key (or SHIFT +
HOME, SHIFT + CTRL + END, etc.).
2. Move cursor to end of current block of filled or empty cells: CTRL + arrow
key.
3. Move cursor to upper left corner of worksheet: CTRL + HOME.
4. Move cursor to lower right corner of occupied portion of worksheet: CTRL +
END.
5. Enter something in a large block of cells: highlight cells, make entry in
formula bar, then press CTRL + ENTER instead of ENTER.
6. Select entire current row(s): SHIFT + SPACEBAR.
7. Select entire current column(s): CTRL + SPACEBAR.
8. Select entire worksheet: SHIFT + CTRL + SPACEBAR.
9. Copy: CTRL + C.
10. Paste: CTRL + V (or ALT + E S for Paste Special).
|
|
|
W 12/8/010
|
HW due:
1. Prepare for your Quick Study quiz (the last one!) by reading this
article. Handwritten notes are encouraged.
2. Read pp. 445-449 carefully. Reading notes are required, as always. It
would probably be a good idea to read this selection twice, since you may be
asked some very picky and specific questions about what the tables and graphs
mean. If there is a quiz (as is quite likely), you may use your reading notes
during the quiz.
3. Continue preparing your Excel task. One or two additional volunteers
selectees may be on the spot today.
|
|
|
Th 12/9/010
|
HW due: Read pp. 450-459
and prepare for one or two quizzes, plus your Excel task.
|
|
|
F 12/10/010
|
HW due: Write pp. 459-461
#8.10, 8.12, 8.17a, 8.18, 8.21. For #8.10, write out the entire statement of
the question, word for word. (I will not subject you to this requirement very
often. However, you must know exactly what is being asked, and you must know
the exact wording with which it is asked.)
We did not have a quiz yesterday because Preston was taking a make-up test,
but we will probably have one or two quizzes today.
|
|
|
M 12/13/010
|
HW due: Read pp. 461-466;
write p. 467 #8.27, 8.29, and also write full corrections to your problems
that were due on Dec. 10. (Solutions are posted at www.hwstore.org.)
|
|
|
T 12/14/010
|
HW due: Write p. 467 #8.30
and the problem below. In each case where you intend to use the normal
approximation, be sure to verify (in writing) that all 3* rules of thumb
discussed in class are satisfied. Show
your work.
Problem: Suppose that the true
proportion, p, of high school
seniors who are supercilious is 0.08.
(a) If we poll 530 randomly selected seniors to see if they are supercilious,
what interval is the central 95% of the sampling distribution of 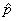 ? ?
(b) What is the interval containing the central 95% if only 50 are polled? (Warning: Part (b) is rather tricky. It
can be answered, but not by using the normal approximation.)
Please give answers to (a) and (b) in the precalculus interval format. For
example, if the answer to part (a) is that 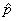 is between 0.068 and
0.092 for 95% of the possible samples, you would give your answer as (0.068,
0.092). is between 0.068 and
0.092 for 95% of the possible samples, you would give your answer as (0.068,
0.092).
* The rules of thumb are 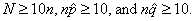
In class: Review day.
|
|
|
W 12/15/010
|
Test (100 pts.) on all recent material. Below is a solution for the second part of
yesterday’s HW problem.
Problem: If p = 0.08 and n = 50,
find the interval containing the central 95% of the sampling distribution of 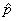 . .
Solution: Since the second rule of
thumb is not met (after all, np is
only 4, and 4 is not greater than or equal to 10), we are not supposed to use
the normal approximation. Instead, we should use the true sampling
distribution of 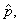 which is binomial. which is binomial.
Let X = binomial r.v. that counts
the number of supercilious seniors (out of 50).
We begin by making a table showing probabilities for various values of X when X is near 4. [Note that 4 is the mean of the distribution, since 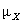 = np = 50(0.08) = 4, and you could use
1-Var Stats L1,L2 ENTER to verify that 4 is the median
as well. Before doing that, you would have needed to put values 0 through 50
in L1 and binompdf(50,0.08) in L2. If the third
parameter is omitted, binompdf returns a list instead of a single value.] = np = 50(0.08) = 4, and you could use
1-Var Stats L1,L2 ENTER to verify that 4 is the median
as well. Before doing that, you would have needed to put values 0 through 50
in L1 and binompdf(50,0.08) in L2. If the third
parameter is omitted, binompdf returns a list instead of a single value.]
However, even though 4 serves as both mean and median of the distribution,
the distribution is not normal, nor is it even symmetric. The distribution is
skew right, as is the case for any
binomial distribution in which p
< 0.5.
Here is the table:
|
|
|
|
k
|
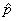
|
P(X = k)
|
|
|
|
|
|
|
======
|
=======
|
=======
|
|
|
|
|
|
|
0
|
0.00
|
0.01547
|
|
|
|
|
|
|
1
|
0.02
|
0.06725
|
|
|
|
|
|
|
2
|
0.04
|
0.14326
|
|
|
|
|
|
|
3
|
0.06
|
0.19932
|
|
|
|
|
|
|
4
|
0.08
|
0.20365
|
|
|
|
|
|
|
5
|
0.10
|
0.16292
|
|
|
|
|
|
|
6
|
0.12
|
0.10625
|
|
|
|
|
|
|
7
|
0.14
|
0.05808
|
|
|
|
|
|
|
8
|
0.16
|
0.02714
|
|
|
|
|
|
|
9
|
0.18
|
0.01102
|
|
|
|
|
|
|
[etc.]
|
|
|
|
|
|
|
|
|
As shown above, the probability that X
= 4, i.e., the probability that 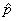 = 0.08, is 0.20365.
By considering an interval from 3 through 5, we see that = 0.08, is 0.20365.
By considering an interval from 3 through 5, we see that 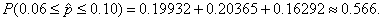 By gradually
widening the interval about X = 4,
each time going the same distance to the left of 4 as to the right of 4, we
eventually obtain By gradually
widening the interval about X = 4,
each time going the same distance to the left of 4 as to the right of 4, we
eventually obtain 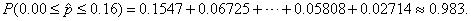 This is the first
interval for which the central span of values has probabilities adding up to
at least 95%. This is the first
interval for which the central span of values has probabilities adding up to
at least 95%.
Answer: The interval [0, 0.16]
contains 95% of the 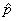 sampling
distribution. Note that we use square brackets, since the endpoints must be
included. sampling
distribution. Note that we use square brackets, since the endpoints must be
included.
Note: Although the  sampling
distribution is skew right, the skewness is very mild. In fact, the estimates
you would obtain by calculating sampling
distribution is skew right, the skewness is very mild. In fact, the estimates
you would obtain by calculating 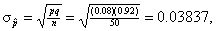 and then using the
Empirical Rule with twice that value (0.0767) to determine the central 95% of
the sampling distribution, would work quite well. When you start with a mean
of 0.08 and add and subtract 0.0767, the interval estimate you obtain is
(0.0033, 0.1567), which is close to the [0, 0.16] that we obtained above. The
binomial approach is still better, however, since it explicitly reminds us
that the and then using the
Empirical Rule with twice that value (0.0767) to determine the central 95% of
the sampling distribution, would work quite well. When you start with a mean
of 0.08 and add and subtract 0.0767, the interval estimate you obtain is
(0.0033, 0.1567), which is close to the [0, 0.16] that we obtained above. The
binomial approach is still better, however, since it explicitly reminds us
that the 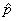 values between 0 and
0.02 are not obtainable. (Why are they not obtainable? The reason is that values between 0 and
0.02 are not obtainable. (Why are they not obtainable? The reason is that 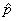 is a discrete random
variable.) Thus, to be correct, we would need to adjust our interval to [0, 0.16]
anyway. is a discrete random
variable.) Thus, to be correct, we would need to adjust our interval to [0, 0.16]
anyway.
|
|
|
Th 12/16/010
|
Wednesday’s
test (blank copy) and the full solution key
with annotations are now posted. See below for a special bonus
opportunity.
Today in class: Optional “Re-Do” Test. Everyone must check in, but then you
may leave if you wish.
The higher of the two scores will count. However, no make-up will be offered
for today’s test, regardless of the reason for your absence. If you missed
yesterday for any reason, today’s test will constitute your make-up test, and
you will have only one score recorded.
Bonus Opportunity: Use the scoring
key below to estimate your score on Wednesday’s test. If you are accurate
within 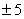 points, you can earn
2 extra-credit points. One way to do this would be to make a “high” set of
estimates and a “low” set of estimates for each question, then add both sets,
and choose the midpoint as your estimated score. points, you can earn
2 extra-credit points. One way to do this would be to make a “high” set of
estimates and a “low” set of estimates for each question, then add both sets,
and choose the midpoint as your estimated score.
The point scoring is as follows:
NAME: Score 4 points if your name
is legible.
Battery bonus: Score 1 point if
you had 4 spare AAA batteries.
1. Score 6 for first blank
(“sampling”), which should be duplicated twice later on.
There is no partial credit for the first blank: “sampling”
is the thing that must be there.
The pattern is 6, [dup.], 3, 2, 2, [dup.], 3, 2, 2,
for a total of 22 points.
Score 1 point for each [dup.] that either matches
another [dup.] or equals the word “sampling.”
2. 3, 1, [dup.], 2, for a total of
7 points
On question #2, score 1 point for [dup.] if the
second and third blanks match, or if the third blank
equals the word “binomial.” Even though “binomial”
does not really fit in the context of the
paragraph, this allows someone who wrote “binomial”
to earn some credit. The word “normal,”
however, does not qualify for credit.
3. 3 + 4 = 7 points
4. 3 points, no partial credit
5. 6 points; deduct 1 point if the
warning about finite 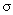 is missing, half a
point for omitting mean of the is missing, half a
point for omitting mean of the
normal distribution approximating the sampling
distrib. of 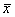 , another half point for omitting s.d. , another half point for omitting s.d.
6. 1 + 1 + 1 = 3 points
7. 4 points; almost any legible
answer that reveals conscious thought will qualify for full credit here
8. 5 points; deduct 1 point if the
word “parameter” is not mentioned at least once
9. 5 for sketch + 5 for 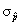 work + 2 for a
believable estimate (anything from 0.01 to 0.3 is acceptable) work + 2 for a
believable estimate (anything from 0.01 to 0.3 is acceptable)
10. 9 points (3 for each rule: 1
for stating the rule, 1 for showing the plugged-in numbers, 1 for check mark)
11. 5 for sketch + 5 for 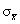 work + 2 for a
believable estimate (anything from 0.01 to 0.3 is acceptable) work + 2 for a
believable estimate (anything from 0.01 to 0.3 is acceptable)
12. 6 points (3 for answering
“no,” 3 for explanation)
|
|
|
F 12/17/010
|
HW due: Attend Lessons and
Carols service at the Cathedral if you possibly can, and practice for your
Excel event.
|
|