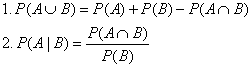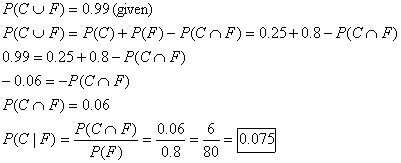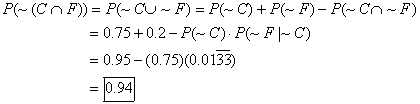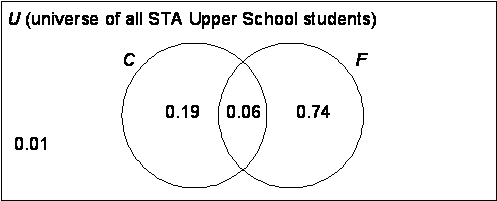|
M 11/1/010
|
No additional HW due. Class
today (or tomorrow, if it rains today) will be outdoors. Your classroom is
the entire Cathedral Close. If you are new to the school, or if you have not
explored the Close much, you will want to read pp. 39-42 (Appendices A and B)
of the STA
School Handbook in preparation for today’s event, which is the
FIRST-EVER STAtistics
PUZZLEMANIA SCAVENGER HUNT EXTRAVAGANZA.
When you arrive at the start of class, you will be given a map of the Close
and a cryptic clue to get you started. The grand prize is boredom repellent
spray, and you will know when you have found it.
After you have solved all the statistics-based puzzles hidden at the various
puzzle locations throughout the Close, you must return to the classroom to
receive your final clue, which will (maybe) allow you to assemble the answers
to the puzzles in such a way as to lead you to the prize. Good luck!
Team 1: Justin, Andrei, Edward, Nick S.
Team 2: Jordan, Julien, Dominique
Team 3: Tip, Ousmane, Preston
Team 4: Brennan, Zeke, Jamie
Team 5: Chick, Alex, Nick R.
Team 6: Andrew, Daniel, Phineas
Ground rules: If another group overhears your strategizing and steals your
ideas, that is not considered cheating. Therefore, you may wish to hold your
brainstorming meetings out of earshot. (Or, if you are clever, you might try
to spread disinformation among the other groups.) However, the following are
not permitted and will be considered cheating:
1. It is cheating (and a violation of school rules) to use cell phones, text
messaging, or walkie-talkies. Play fair, gentlemen!
2. It is cheating and dishonorable to disrupt, move, steal, hide, or
otherwise tamper with any box containing puzzle cards. You need to leave the
boxes undisturbed for the next team to find.
3. It is cheating, not to mention rude and disruptive, to shout or run
indoors. Behave properly indoors. Outdoors is where you can let off some
steam.
4. It is cheating to physically detain or harass other team members. You must
give everyone a fair chance at the prize.
Permitted strategies you might want to consider:
1. It might be wise to have a trailing lookout to guard against having other
teams follow you.
2. You may use the classroom (MH-103) as a location for sending and receiving
e-mail.
3. I recommend staying together as much as possible. Three brains are much better than one. Since everyone
will eventually find all the puzzle problems, don’t think you are winning
just because you found all the puzzle locations first. The final puzzle,
where you have to assemble the parts to find the prize, is a doozy.
4. Trading information with other groups (“We’ll tell you where ____ is if
you tell us where ____ is”) is permitted.
|
|
|
T 11/2/010
|
No additional HW due today.
Mr. Hansen needs a day to recover (after waking up at 3:30 yesterday morning
for the puzzlemania). However, older assignments, especially assignments that
have been covered in class, may be rescanned.
If anyone other than the teams that have already won prizes would like to
submit worked-out solutions to the
four puzzle problems, small consolation prizes will be available.
|
|
|
W 11/3/010
|
HW due: Prepare for quiz on
Monday’s
Quick Study article.
|
|
|
Th 11/4/010
|
HW due: Read pp. 279-296,
including all four property explanations on p. 296. Do not read ahead to the tan boxes on p. 298 until we have had a
chance to discuss what they mean.
|
|
|
F 11/5/010
|
No school (teacher work
day).
|
|
|
M 11/8/010
|
Practical Double Quiz:
“Excelcise” (see 10/28 calendar entry) with a 5-minute time limit. Those who
take the quiz today and do not pass will have to come in before or after
school to pass. Practice, practice, practice!
HW due: Re-do your take-home test
from two weeks ago. If there are some questions that you are certain are
perfect already, you may leave them as they are, but for the other ones,
please rewrite them on a fresh copy of the test. Working with classmates,
Wikipedia, textbook, etc., will be permitted as long as you use your own words in the essay answers. Outright
copying or blatant paraphrasing is still considered an honor issue.
Note: It is possible that some of
the same questions that were spot-checked on the first pass will be spot-checked
again.
After receiving an extremely polite student request, I have decided to tell
you which 3 problems were scored in the spot check the first time around.
They were as follows:
#2b (3 points for saying that we apply judgment when looking for points with
large positive or negative residuals)
#7a (3 points: 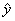 , which must be looped, is the dependent variable, not y, and the variables x and y must be defined in words) , which must be looped, is the dependent variable, not y, and the variables x and y must be defined in words)
#8c (2 points for saying “Yes” + 2 points for saying that exponential
equations are easily solved, or similar words to that effect)
Notes on individual test questions:
4. Note that the Greek symbol should have been displayed as 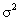 , not s2.
The problem was a technical Web browser issue that affected some users but
not others. The glitch has now been corrected. , not s2.
The problem was a technical Web browser issue that affected some users but
not others. The glitch has now been corrected.
7(a). You must define the two variables used in the LSRL. Remember, slope and
intercept are parameters of the
LSRL model, not variables. The two variables are x, the independent variable, and y (or 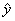 ), the dependent variable. If you define ), the dependent variable. If you define 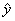 instead of y, that is fine, but then you must use
the word “predicted” in your definition. For example, in a LSRL that shows the
relationship between hours of study (x)
and GPA (y), we would define
variables as follows: instead of y, that is fine, but then you must use
the word “predicted” in your definition. For example, in a LSRL that shows the
relationship between hours of study (x)
and GPA (y), we would define
variables as follows:
x = study time (hrs.)
y = actual GPA (100-pt. scale)
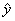 = predicted GPA
(100-pt. scale) = predicted GPA
(100-pt. scale)
I am not expecting both y and 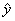 to be defined.
Choose one or the other, plus x,
and that will be fine. to be defined.
Choose one or the other, plus x,
and that will be fine.
7(b). Despite the instruction saying that you would need to do more than
calculate the r value, a large
majority of students did not take the hint. A residual plot must be sketched
in this problem, and you must say what the residual plot is telling you.
7(c). Learn this wording, which is what will be expected from you on the AP
exam:
“The slope, ___________ , gives the predicted change in minimum socially acceptable female age for each increase of 1 year in the
man’s age.”
I have italicized the words
that students often forget to include. You may copy my wording for this
question only. You must understand that the slope does not tell you what the
woman’s age is, given the man’s age, nor does the slope tell you what the
actual change in female age is as men grow older. The slope tells you the predicted change, according to the
LSRL model, for each change of +1 unit in the dependent variable.
However, if you write, “The slope tells you the predicted change, according
to the LSRL model, for each change of +1 unit in the dependent variable,” you
still will not earn full credit. The reason is that on the AP exam, you have
to write your interpretation of the slope in
the context of the problem. Use the model in the box above, and you will
be safe.
|
|
|
T 11/9/2010
|
HW due: Read the topics
listed below; write pp. 286-287 #6.1, 6.10, and parts a, b, and c of the
problem below.
Problem: A chest of drawers has
three drawers, each of which contains exactly two coins. One of the drawers
has two gold coins, one has two silver coins, and one has both a gold and a
silver coin. A drawer is selected at random, and a coin is withdrawn at
random from that drawer (without peeking).
(a) List the sample space of outcomes for the coin.
(b) Make a tree diagram for all possible outcomes. There should be 6 paths in
your tree diagram, since the choice of drawer can be made in 3 ways, and the
choice of coin can be made in 2 ways.
(c) List the sample space of outcomes for the coin and its “partner coin” in
the same drawer, but list the outcomes in such a way that all possibilities
are equally likely. Use a capital letter for the coin selected, and a lower
case letter for the partner coin in the same drawer. Hint: It would be an error to say {Gg, Ss, Gs, Sg}, because those
possibilities are not all equally likely. You may have to use subscripts to
keep track of the coins. Refer to your tree diagram, and you should be able
to get the right answer.
In class: Another victim volunteer or two will perform the Excelcise.
Then we will choose topics for our probability simulation/education project,
with group 1 having first choice of topics, group 2 second choice, and so on.
Any group that is not happy with its topic can negotiate a replacement topic
with Mr. Hansen.
Group 1: Nick R.-S., Justin, Dominique
Group 2: Alex, Andrew, Phineas
Group 3: Daniel, Chick, Preston
Group 4: Jamie, Julien, Brennan
Group 5: Edward, Zeke, Jordan
Group 6: Nick S., Tip, Andrei, Ousmane
The vertical line character, | , is to be read as the word “given.” Here are
a dozen topic ideas to choose from:
A. Monty Hall problem: P(winning prize | switch) = 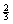 , not , not 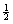 . .
B. Chest of drawers problem: In Version
A, P(second coin is gold | first
coin is gold) = 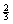 , not , not 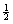 . .
C. Two-dice problem: P(snake eyes |
at least one “1”) = 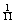 , not , not 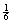 . .
D. Birthday paradox: P(at least one
shared birthday) > .5 whenever 23 strangers are in a room.
E. P(either TTTTTT or HHHHHH, or
both, occur in 100 random coin flips) > 0.8.
F. P(patterns HHHHTTTT, TTTTHHHH,
TTTTTTT, or HHHHHHH occur in 100 random coin flips) > 0.74.
G. P(patterns TTTT, HHHH, HHHTTT,
and TTTHHH all occur in 100 random
coin flips) > 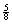 . .
H. Which pattern is more likely when flipping coins, HHHHH or THHTTH?
J. P(at least one “1” occurs when 5
dice are rolled) 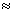 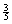 , not , not 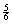 . .
K. P(first “1” in dice rolling
occurs on or after the 13th try) > 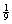 , though intuition suggests < , though intuition suggests < 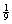 . .
L. P(third card drawn from a deck
is a 3 | first two cards drawn are face cards) = 0.08, not 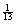 . .
M. If P(HIV positive | DC resident)
= 0.02 and HIV-positive people are randomly distributed as restaurant patrons,
then P(at least one fork you
received while dining in DC was most recently used by an HIV-positive diner)
= .554 if you were to eat out on 40 independent occasions.
|
|
|
W 11/10/010
|
HW due: Read pp. 302-310
twice and prepare for your Quick
Study quiz; write p. 302 #6.25 (personal paper) and the assignment below
(group submission). If the group leader is absent for any reason, he must
deputize someone to hand in the group submission.
Group Problem: Attempt a
one-paragraph proof of the correct answer to your group’s problem. A diagram
alone is not sufficient; you need some grammatically correct text as well.
Correctness of answers is not required at this point; Mr. Hansen simply needs
to verify that you have the correct concepts in mind before you start
teaching other people.
Group 1, Topic A: Nick R.-S., Justin, Dominique
Group 2, Topic B: Alex, Andrew, Phineas
Group 3, Topic D: Daniel, Chick, Preston
Group 4, Topic C: Jamie, Julien, Brennan
Group 5, Topic H (tentative choice): Edward, Zeke, Jordan
Group 6, Topic E: Nick S., Tip, Andrei, Ousmane
Group 6 will definitely need a spreadsheet simulation, because computing the
probabilities with formulas or diagrams is essentially impossible. You can
download a sample spreadsheet here.
|
|
|
Th 11/11/010
|
HW due: Read pp. 313-320
and the exercise with explanation below; write pp. 311-313 #6.36, 6.40, and the
problem below (after the explanation).
Exercise: Chant (literally chant,
out loud) the following sentence a minimum of 10 times.
Independence is not the same as being mutually exclusive (i.e., disjoint).
Independence is not the same as being mutually exclusive (i.e., disjoint).
Independence is not the same as being mutually exclusive (i.e., disjoint).
Independence is not the same as being mutually exclusive (i.e., disjoint).
Independence is not the same as being mutually exclusive (i.e., disjoint).
Independence is not the same as being mutually exclusive (i.e., disjoint).
Independence is not the same as being mutually exclusive (i.e., disjoint).
Independence is not the same as being mutually exclusive (i.e., disjoint).
Independence is not the same as being mutually exclusive (i.e., disjoint).
Independence is not the same as being mutually exclusive (i.e., disjoint).
If you are embarrassed to do this indoors, then do it outdoors somewhere
where nobody will hear you. Or, you could call a friend on the phone and
chant the saying together, or taking turns with each chanting to the other.
Explanation: Disjoint events (often called mutually exclusive events) are
events that cannot both occur. For example, if you draw a single card from a
well-shuffled deck, the card cannot be both a spade and a club; it must be
one or the other (or one of the red suits). Therefore, P(spade or club) = P(spade)
+ P(club) = 0.25 + 0.25 = 0.5,
since there is no “overlap” between spadeness and clubness on a single draw.
We can illustrate mutually exclusive (disjoint) events with a Venn diagram as
shown on p. 285, Figure 6.3(d).
Independent events are something
completely different. THERE IS NO
STANDARD WAY TO SHOW INDEPENDENCE WITH A VENN DIAGRAM. Independence of
two or more events means that the events do not affect each other’s
probabilities. For example, a die roll has a probability of 1/6 of being a
“6,” regardless of the outcome of a coin flip. Therefore, we say that the
event of rolling a “6” and the event of getting tails on a coin flip are
independent events.
Are “king” and “red” independent events if you draw a single card from a
well-shuffled deck? Well, P(king) =
4/52, since there are 4 kings in a standard 52-card deck, and P(king | red) = 2/26, since there are
2 kings out of the 26 red cards in a deck. Since 4/52 and 2/26 are equal, the
“redness” has not affected the probability of obtaining a king. The events
are independent.
Are “clubs” and “red” independent events? How about “clubs” and “black”? NOTE THAT THE ANSWER HAS NOTHING TO DO
WITH WHETHER THERE IS ANY OVERLAP BETWEEN CLUBS AND RED CARDS, OR BETWEEN
CLUBS AND BLACK CARDS. Instead, the question we ask ourselves is whether
knowing the color of the drawn card affects our assessment of the probability
of drawing a club.
P(club | red) = 0, since there are
no red clubs. (All clubs are black.) On the other hand, P(club | black) = 0.5, since half the black cards in the deck are
clubs, and the other half are spades.
But notice the key issue here: P(club)
= 0.25. In other words, the regular (“unconditional”) probability of drawing
a club is 1 in 4, or 0.25. Does knowing the color of the drawn card change
our assessment?
Yes, it does. P(club | red) is less
than 0.25, namely 0, and P(club |
black) is more than 0.25, namely 0.5. Therefore, we can conclude two things:
1. “Clubs” and “red” are NOT independent events.
2. “Clubs” and “black” are NOT independent events.
Problem: Let A and B be two events
with nonzero probability. (For example, you could imagine that A is the event that Mr. Hansen is
wearing a pink shirt, and B is the
event that Kanye West wins the 2011 Grammy for Best Male Vocalist. Or, make
up two other events, as long as they both have nonzero probability.) Also
assume that A and B are disjoint, in other words, that P(A and B) = 0. Prove that regardless
of what events A and B actually are, A and B are not
independent.
A “math proof” is not required. In fact, Mr. Hansen would rather see a
thoughtful sentence or two of explanation.
|
|
|
F 11/12/010
|
HW due: Read pp. 323-328
(top). Omit the Law of Total Probability and Bayes’ Rule (pp. 328-332). Then
write pp. 332-333 #6.61 and the following:
1. Compute P(A), P(B), P(A | B), P(A 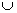 B), and P(A B), and P(A 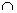 B). Determine whether events A
and B are disjoint, independent,
neither, or both. Show work. B). Determine whether events A
and B are disjoint, independent,
neither, or both. Show work.
A = the event of rolling an even
number with a fair die
B = the event of rolling a “2” with
a fair die
2. Compute P(C), P(D), P(C | D), P(C 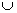 D), and P(C D), and P(C 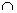 D). Determine whether events C
and D are disjoint, independent,
neither, or both. Show work. D). Determine whether events C
and D are disjoint, independent,
neither, or both. Show work.
C = the event that free dress
occurs on a randomly chosen school day (assume the year has 152 school days, of
which 6 are free-dress days)
D = the event that Mr. Hansen’s
random integer generator selects student #7 in HappyCal to go to the board at
least once on a certain day
For event D, assume that Mr. Hansen
always selects 3 students each day, and assume that all 14 students are
always present. Also assume that each student has the possibility of being
selected each time, i.e., that it is possible for a student to be summoned to
the board as many as 3 times in a single day.
|
|
|
M 11/15/010
|
HW due: Three-part
assignment.
1. Read pp. 335-343.
2. Then, write p. 346 #6.80a, using the instructions and helpful hints given
below.
3. Correct all recent HW answers using the solution keys posted at hwstore.org. Some of these assignments may be
re-scanned today during our review session, and if you have not corrected
them, you will not earn credit. Please use a different color of ink for your
corrections.
Instructions and hints for #6.80a:
Be sure to write out your proposed simulation procedure before you execute
it. Several sentences of description are required. Think, for example, of
what you wrote several weeks ago when you described a randomization procedure
for selecting group leaders and group members. This is a similar task, except
that you are describing how to assign random events to the selection of taxi
license applicants. Think of a desirable number (say, 18, since you are
either 18 or are looking forward to being 18 soon) that designates the
“single-license” applicant of interest. You could, for example, use either of
these approaches:
Example Methodology (A):
Consult a random digit table, such as the one on pp. 814-815, and take digits
in pairs to indicate chosen applicants, starting on row 27 and never reusing
any portion of the table. Declare that 00-04 = applicant #1, 05-09 =
applicant #2, and so on, until 95-99 = applicant #20. Also declare that
applicants #1 through #6 have applied for 3 licenses each, #7 through #15
have applied for 2 licenses each, and #16 through #20 have applied for 1
license each. For each iteration, clearly record in pencil which applicants
are selected until the 10 licenses are exhausted, and record “SUCCESS” if
applicant #18 gets a license, “FAILURE” if applicant #18 does not get a license.
After 20 iterations, compute the sample proportion of successes by the
formula 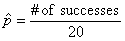 , and state that , and state that 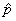 is an estimate of
the true probability of success for applicant #18. is an estimate of
the true probability of success for applicant #18.
Example Methodology (B):
Use a coin flip to indicate a 0 or a 1 (heads = 0, tails = 1), which will
signify the first digit. Then use a single digit from a random digit table to
signify the second digit. Start on row 56, and be careful never to reuse any
portion of the table. These two events together—coin flip followed by random
digit—will produce outcomes from 00 through 19 designating a successful
applicant, and as long as we number the taxicab license applicants as 00-19
instead of 01-20, everything will turn out well. Declare that applicants
00-05 have applied for 3 licenses each, 06-14 have applied for 2 licenses
each, and 15-19 have applied for 1 license each. For each iteration, clearly
record in pencil which applicants are selected until the 10 licenses are
exhausted, and record “SUCCESS” if applicant #18 gets a license, “FAILURE” if
applicant #18 does not get a license. After 20 iterations, compute the sample
proportion of successes by the formula 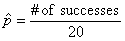 , and state that , and state that 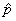 is an estimate of
the true probability of success. is an estimate of
the true probability of success.
There are many, many approaches you could take. The one approach you may not take is to say, “Select a random
integer 1-20 from the calculator using the randInt() function.” The reason is
that on the AP exam, you are required to use the furnished random digit
table, similar to the one on pp. 814-815, when performing your simulations.
If you are not able to think of a creative randomization procedure, you may
use either of the methodology examples I gave above (A or B, your choice) as
your starting point. That will be fine. Warning:
You do have to rewrite the procedure, however, since you must practice
writing out the steps.
One year, when teaching AP Statistics, I foolishly permitted my students to
discuss their simulation procedures instead of actually writing them out.
Then, on the AP exam, most of them fumbled the simulation question because
they had never actually practiced writing out the steps for a simulation. I
won’t repeat that mistake. Even if all you are doing, for now, is copying one
of my example methodology writeups above, you have to write out all the
words. Standard abbreviations (“est.” for estimate, “tbl.” for table, etc.)
are permitted, of course.
In class: Review for test.
|
|
|
T 11/16/010
|
Test (100 pts.) on Chapter 6. For this test, you will not be required to write
out simulation methodologies from scratch. (We will do that later in the
week.) However, you may be asked to execute a simulation methodology to come
up with a 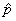 value. You also have to know what value. You also have to know what 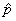 is called and what
its purpose is. (Answer: is called and what
its purpose is. (Answer: 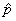 = the sample
proportion, which is an estimate of the true probability.) = the sample
proportion, which is an estimate of the true probability.)
The only material from earlier in the year that may be tested will be z scores and percentiles, since a
percentile gives the probability that a randomly chosen member of the
population is below the data item of interest. The probability formulas you
need will be furnished for you on an AP-style formula sheet (see p. 17 of this
.PDF file, but note that the probability formula page itself is labeled
as “13” in the lower right corner of the page).
Note: There are really only 3
formulas that you need. The first two are on the AP formula sheet and are
reproduced below with explanations. The third is the famous formula 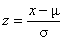 , which is not on the AP formula sheet. (You are just
supposed to know it all year long.) , which is not on the AP formula sheet. (You are just
supposed to know it all year long.)
Probability Formulas from the AP
Formula Sheet:
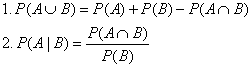
Explanations:
You are supposed to be able to do algebra to rewrite formula 1 as
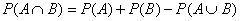
if the need arises. Also, you are supposed to be able to realize that if A and B are disjoint events, then formula 1 simplifies to give the
second tan box on p. 298. I do not
recommend memorizing the second tan box on p. 298, however, because if you
are not careful, you might accidentally start applying it in situations where
the events are not disjoint.
In a similar way, you are supposed to be able to do algebra to rewrite
formula 2 as
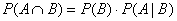
if the need arises, and it often does. Note that since 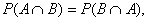 we can swap the
roles of events A and B to get the equivalent formula we can swap the
roles of events A and B to get the equivalent formula
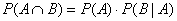 , which is actually more useful. This matches the tan box
on p. 325. , which is actually more useful. This matches the tan box
on p. 325.
In words: “To find the probability that two events both occur, multiply the
probability of the first event by the conditional probability of the second
event given the first event.” This is common sense, actually. To find the
probability of drawing two aces in a row from a shuffled deck, we can’t
multiply the probability of getting an ace on a single draw, which is 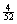 , by itself. Instead, we must multiply , by itself. Instead, we must multiply 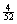 by by 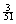 , since after the first ace has been drawn, there are only
3 aces among the remaining 51 cards. Answer: P(two aces when cards are drawn without replacement) = , since after the first ace has been drawn, there are only
3 aces among the remaining 51 cards. Answer: P(two aces when cards are drawn without replacement) = 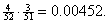
If, on the other hand, you were to ask for the probability of drawing two
aces in a row with replacement,
then you would be talking about independent events, assuming that you shuffle
the deck in between. Answer: P(two
aces when cards are drawn with replacement) = 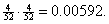 Not much of a difference, you say? Actually,
that’s more than a 30% improvement in the probability. Casinos can and do
exploit discrepancies between what people perceive the probabilities to be
and what they actually are. For them, the name of the game is money. For you,
the name of the game is understanding the principles and getting the answers
right. Not much of a difference, you say? Actually,
that’s more than a 30% improvement in the probability. Casinos can and do
exploit discrepancies between what people perceive the probabilities to be
and what they actually are. For them, the name of the game is money. For you,
the name of the game is understanding the principles and getting the answers
right.
Before taking the test, you should shake the “Lower School rule” out of your
head. Many of you may have (erroneously) learned that
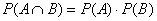 , but what you must remember is that , but what you must remember is that 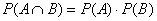 if and only if events A and
B are independent. In the real
world, events are usually not independent, which means that your “Lower
School rule” is usually useless. Similarly, the tan box at the bottom of p.
316, which you may also have learned in earlier classes, works if and only if all the events are
independent. if and only if events A and
B are independent. In the real
world, events are usually not independent, which means that your “Lower
School rule” is usually useless. Similarly, the tan box at the bottom of p.
316, which you may also have learned in earlier classes, works if and only if all the events are
independent.
Finally, suppose that I ask you to check whether two events are independent.
Since “if and only if” means the same as the “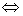 ” symbol (logical equivalence symbol), we can use the fact
that ” symbol (logical equivalence symbol), we can use the fact
that 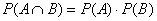 if and only if events A and
B are independent to give us a
simple check for independence. Multiply the probability of A by the probability of B. If the answer equals if and only if events A and
B are independent to give us a
simple check for independence. Multiply the probability of A by the probability of B. If the answer equals 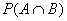 , then congratulations, you have proved independence. If
not, you have proved lack of
independence. It’s as simple as that. , then congratulations, you have proved independence. If
not, you have proved lack of
independence. It’s as simple as that.
Example problem:
Let C = event that a randomly
chosen STA Upper School student is a competent student of probability,
someone who reliably gets correct answers to probability questions. Let F = event that a randomly chosen STA
Upper School student has organized his probability knowledge around Lower
School probability formulas and techniques. Suppose also that P(C)
= 0.25, P(F) = 0.8, and P(C or F) = 0.99. Determine
(a) P(C | F)
(b) the probability that a randomly chosen STA Upper School student is both
competent and focused on Lower School probability formulas
(c) the probability that a randomly chosen STA Upper School student is not
both competent and focused on Lower School probability formulas, and
(d) whether C and F are independent.
Solution:
(a)
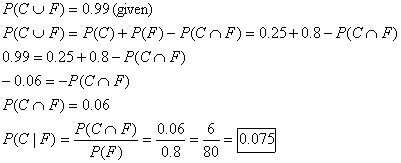
(b) 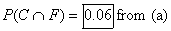
(c) 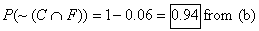
Alternate method for (c), much harder but rather interesting:
First, note that 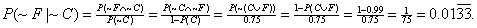
Therefore,
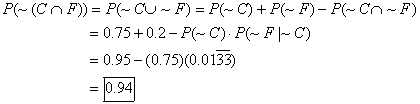
Simplest method for (c), useful in all problems of this type, is to make a
Venn diagram:
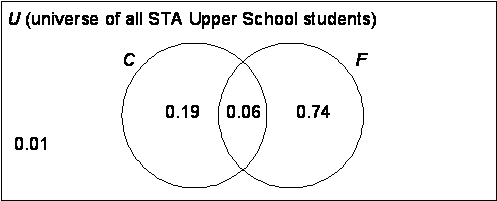
With a Venn diagram, part (c) and many other questions can be answered by
inspection. We set the region outside both circles to have probability 0.01,
since it was given that C union F accounts for 99% of the universe.
From part (a), we know that the “overlap” region for the two events has
probability 0.06. Then, adjust the other regions so that C has a total probability value of 0.25, and F has a total value of 0.8.
While we are at it, see if you can compute the following probabilities by
inspection:

(d) We know from (a) and the Venn diagram that 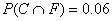 . However, . However,
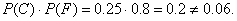 Conclusion: not independent. Conclusion: not independent.
|
|
|
W 11/17/010
|
HW due: Re-do yesterday’s test in its entirety, including the
expected value bonus in #4.
Expected value is nothing more than the probability-weighted average of the
outcomes. For example, if I agree to give you 4:1 odds for your ability to
roll a 3 with a single die, your expected value per dollar that you wager is
given by
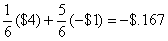 . Since the expected value to you is negative, this is
clearly an unfair game! . Since the expected value to you is negative, this is
clearly an unfair game!
Problems will be spot-checked.
|
|
|
Th 11/18/010
|
HW due: Provide some anonymous feedback on your STAtistics experience;
write pp. 344-346 #6.78, 6.79, following the special instructions below.
Notes for #6.78: Please write “ALL
COUNTS ARE THOUSANDS” before starting this problem. That will save you a lot of
time. Also, when writing the “setup” of each problem, you are encouraged to
use probability notation. Setups are required, as always, but you are wasting
time if you recopy all the words that the book provides. Instead, follow this
example:
6.78(i)
 . .
The “n choose r” function, indicated by parentheses, is something you learned
in Algebra II and Precalculus. If you have forgotten how to compute these,
the keystrokes are [first number] MATH PRB 3 [second number] ENTER.
Notes for #6.79: The methodology
is provided for you; all you have to do is execute and record your outcomes.
If your last name begins with B through J, begin your simulation on row 1 of
the random digit table on pp. 814-815. Last names K-R should start with row
29, and last names S-Z should start with row 67.
|
|
|
F 11/19/010
|
HW due: Read pp. 357-365;
write pp. 365-366 #7.8, 7.9abcdef. Part (f) is done for you as an example
below, so that you can see the amount of work that is expected.
7.9(f) P(at least 10 unbroken) = P(unbroken count 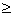 10) = P(broken count 10) = P(broken count 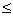 2) = P(y 2) = P(y
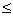 2) = 2) = 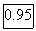 from (c) from (c)
Also, prepare for your Quick
Study quiz. After today, we have only two more of these quizzes, one on
Dec. 1 and one on Dec. 8.
Finally, if you did not finish yesterday’s simulation (#6.79), download this spreadsheet and compute a 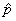 value (sample
proportion) for part (a). Be sure to record how many iterations you performed
(n value (sample
proportion) for part (a). Be sure to record how many iterations you performed
(n 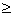 20). In class, we
will combine the sample proportions from all the students to get a fairly accurate
estimate of p, the true probability
that more than 5 pairs must be treated before a conclusion can be reached. 20). In class, we
will combine the sample proportions from all the students to get a fairly accurate
estimate of p, the true probability
that more than 5 pairs must be treated before a conclusion can be reached.
|
|
|
M 11/22/010
|
HW due: Read pp. 367-383.
We will use the abbreviation “r.v.” for “random variable” throughout the
course. In addition to your required reading notes, make the following markups
(in pencil or pen, your choice) on pp. 375 and 377:
Underneath the tan box on p. 375,
write . . .
Mean of r.v. = 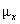 = expected value =
“probability-weighted average of all possible outcomes” = expected value =
“probability-weighted average of all possible outcomes”
Underneath the tan box on p. 377, write
. . .
Variance of r.v. = 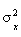 =
“probability-weighted average of squared deviations from the mean” =
“probability-weighted average of squared deviations from the mean”
In class on Friday, we discussed the concept of a weighted average, and we
discussed how the weights could be probabilities. In a weighted average, we
always divide by the sum of the weights. If that is true, why is it that the
formulas in the tan boxes on pp. 375 and 377 have no denominators showing a
sum of weights?
|
|
|
T 11/23/010
|
HW due: Write pp. 383-384
#7.27-7.32 all. In #7.32, be sure to show your work when calculating 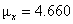 and and 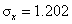 . (Three decimal places of accuracy are required for the
final answers. Do not round any values until you reach the end. Today is
probably the last day, except for your test, on which you will have to show
all the work.) Also, since this is the last day before our long break, I
thought you might enjoy an interesting change of pace. Read this
article about how posture may affect testosterone levels and this
article about the surprising neurological links between addiction, marriage,
and child-rearing. . (Three decimal places of accuracy are required for the
final answers. Do not round any values until you reach the end. Today is
probably the last day, except for your test, on which you will have to show
all the work.) Also, since this is the last day before our long break, I
thought you might enjoy an interesting change of pace. Read this
article about how posture may affect testosterone levels and this
article about the surprising neurological links between addiction, marriage,
and child-rearing.
There will be no quiz on the articles, but reading notes are required. You
don’t want to be uninformed if we have a class discussion on either or both
of these articles.
|
|
|
W 11/24/010
|
No school.
|
|
|
Th 11/25/010
|
No school (Thanksgiving).
|
|
|
F 11/26/010
|
No school.
|
|
|
M 11/29/010
|
HW due: Read pp. 386-416.
If you have additional time during the long break, you may wish to work ahead
on the next two days’ assignments. Many of the problems have answers in the
back of the book.
|
|
|
T 11/30/010
|
HW due: Write pp. 395-397
#7.46, 7.54, 7.55, 7.56, 7.61, 7.62.
|
|