|
F 10/1/010
|
No class (Form VI retreat).
|
|
|
M 10/4/010
|
No additional HW is due.
However, please make sure that your previously assigned problems are well
organized and as complete as possible.
|
|
|
T 10/5/010
|
HW due: Read pp. 159-192
including all examples but skipping over the pages of exercises. This is a
net of about 25 pages, but you can spread it over two nights. Then write the
following questions, showing your work where appropriate. (Yes, I realize
that some of the computations are easy enough to do in your head. That
doesn’t matter. You still need to “teach” the material to the reader as
illustrated in class yesterday.)
pp. 167-168 #21a*bc and #4.23 [see note below]
p. 175 #4.31
pp. 183-184 #4.36, #4.40, #4.41.
* For #21a on p. 168, go ahead and actually compute the mean when combining
Los Osos and Morro Bay. This is called a weighted
mean or a weighted average.
In class: Substitute teacher will show you this 27-minute
video on normal distributions. You
are required to watch the video twice.
If the substitute teacher needs help getting popup windows to display, I
trust that you can lend a hand. The video is #4 in the series of 26
statistics videos entitled “Against All Odds.”
On the second pass, please ask the substitute teacher to skip over the
beginning credits (the first 1:45 of the video), the segment featuring the
Boston Beanstalks (from about 15:21 to 17:31), and the long interview with
Stephen Jay Gould (20:29 to 24:45). Gould died in 2002, for what it’s worth.
When you make those cuts, the running time will be 27 minutes for the first
pass and 19 minutes for the second pass. Therefore, you should be able to accomplish
both viewings during the 50-minute class period.
If for some reason you are unable to watch the video a second time at school,
I expect you to watch it a second time at home. This is a great way to learn!
You may be a little bored, but you will also notice that you pick up details
on the second time that you missed the first time.
Note-taking during the video is encouraged, since if there is a quiz at a
later date on the video, you will be permitted to use your notes.
|
|
|
W 10/6/010
|
No additional written HW is
due, but be sure that all of your previously assigned problems are complete
and well organized. Make sure you have read through p. 192, with reading
notes.
|
|
|
Th 10/7/010
|
Quiz (10 pts.) on last
Tuesday’s Quick Study and this
Tuesday’s Quick Study.
HW due: Read pp. 199-207; write pp. 207-208 #5.1, 5.2, 5.4.
|
|
|
F 10/8/010
|
No school (faculty
professional day).
|
|
|
M 10/11/010
|
No school (holiday).
|
|
|
T 10/12/010
|
HW due: There are two
required parts. People who turned in a randomization methodology last
Thursday are exempt from having to redo #1 (even if it was not very good),
but everyone needs to do #2.
1. Write up a randomization
methodology for choosing groups and group leaders. There are to be 6 groups,
with 3 students in each group except for a single group of size 4.
Student names are as follows: Alex, Andrei, Andrew, Brennan, Chick, Daniel,
Dominique, Edward, Jamie, Jordan, Julien, Justin, Nick R., Nick S., Ousmane,
Phineas, Preston, Tip, Zeke.
Important: Your methodology must be
neat and legible. Somewhere between a half page to a full page will be
required, depending on how elaborate your steps are. For example, writing
“Draw names from a hat; the first 6 names chosen will determine the group
leaders” is not nearly enough to write, because two people executing the same
instructions from the same sequence of drawn names could easily come up with
many different reasonable ways of interpreting the instructions. One person
may fill group 1 before going on to groups 2 through 6, whereas another
person may fill all the groups simultaneously (in the manner of dealing cards
from a deck). One person may stir up the names in the hat before drawing a
new one, and another may leave the names in the hat in essentially their
original order (thus biasing the drawing). One person may write only first
names on the hat, and another may write full legal names. One person may
discard each entry as it is drawn, while another may return names to the hat
each time and ignore duplications if they occur. One person may decide that
the final name assigned is determined by default, while another may insist on
drawing the final name as a cross-check to make sure that no errors have
occurred. One person may fill the even-numbered groups first, while another
may fill the groups in reverse order from 6 to 1, and a third person may wait
until the end to number the groups. One person may perform the drawing in
secret, while another insists on having the entire process observed by the
class so that everyone can agree that the process was fair. One person may
use numbers instead of names, taking care to underline the 6 so that it is
distinguishable from the 9, and another may insist on using full legal names.
One person may specify that the slips of paper are of uniform size and shape,
while another specifies that the pieces of paper are randomly sized but are
numbered or marked in random order in order to preserve randomness.
Do you see how many choices remain? You can probably come up with even more
questions that are not answered by the initial terse instruction.
If your instructions are in any way unclear, you will need to rewrite them to
remove all ambiguity. Also, please try to come up with something more
creative than drawing slips of paper from a hat.
If you submitted a methodology writeup last Thursday, you are exempt from
this task (even if your writeup was not very good), but you are welcome to
try again anyway. The skill to learn here is the skill of organizing your
rules clearly, so that any reasonable person could implement the rules or,
equivalently, read the rules and then act as a judge to determine whether
somebody else had implemented them properly. If the answer to the question,
“Is this permitted by the rules?” is, “I don’t know; let’s ask Mr. Hansen for
a ruling,” then your methodology is not yet clear enough.
Does this skill have real-world value? Definitely . . . if you plan on going
into engineering, law, computer science, medicine, business management,
accounting, or almost any other field where following certain rules and
procedures is important. As you become more senior in your field, your job
will consist less of following
rules and more of writing rules and
guidelines for other people in the profession to follow.
“But wait, Mr. Hansen! I want to be an artist, a small-business entrepreneur,
or a professional athlete. This is a waste of my time!” Admittedly, the skill
of writing detailed rules is generally not important in those professions.
However, I still want you to learn the skill, if for no other reason than to
help you recognize when other people have done it poorly.
2. Read pp. 210-217 (taking care to
ignore the tan box on p. 213, which we will never use); write pp. 217-218 #5.17.
|
|
|
W 10/13/010
|
Quiz (10 pts.) on yesterday’s Quick
Study. By now you should know how to score high on these quizzes. Forget
about memorizing trivia. Instead, read the article with your new “statistics
student” eyes. What are the important aspects of the article from a
statistics standpoint? What is missing, if anything? What is the conclusion,
and is it statistically significant?
HW due: Each group must submit an exploratory data analysis project proposal
(approximately one page) with milestones. If you cannot think of something
exciting to do, you can always analyze my commuting data, which now has
nearly six weeks’ worth of morning drama distilled down to a single table.
Ground rules: No exemption if your
group leader is absent today (or yesterday, for that matter). Life goes on.
Choose a deputy and soldier forth. If you don’t know or don’t remember what
group you are in, use some of that networking skill that your generation is
so savvy with.
More ground rules: Plan on
collecting at least 30 data points for at least 2 variables of interest (more
would be better). Describe how you would conduct univariate (histogram,
boxplot, etc.) and bivariate (scatterplot, regression, etc.) data analyses in
your search for interesting patterns. If you have any research questions that
would guide or motivate your data explorations, you may mention them as well,
but that is not required at this point. For the most part, we will postpone
doing inferential statistics until the second semester.
Opinion surveys are permitted, but if you gather opinions, be sure to collect
at least two quantitative variables as well so that you will be able to run
some linear regressions.
When listing your milestones, give the estimated date by which each of the
following will be complete: final methodology document, data gathering,
spreadsheet compilation, consultation with Mr. Hansen, first draft and
feedback from Mr. Hansen (optional), final draft, and project submission.
Your final report should be 3-5 pages, plus appendices for your raw data (one
row per record), survey instruments (if any), and any artifacts of the
data-gathering process such as consent forms, data recording forms, and
instruction forms. There will be a small point deduction for each spelling
and typographical error, as well as a deduction for use of color graphics.
(Any good report should still be able to tell its story with black-and-white
graphics, even if they do not look quite as appealing.)
The job of the group leader is to keep everyone working productively and to
be the “heavy” when people miss meetings. The group leader must attach a
short report to the final report stating what each person’s contribution was (in
specific detail) and recommending a
division of points.
|
|
|
Th 10/14/010
|
HW due: Read first tan box
on p. 228 and the review material below; write p. 234 #5.37, 5.38.
You were taught how to make a residual plot in precalculus. In case you have
forgotten, the instructions are reproduced below.
Residual Plot Quick Review
Every time you perform a regression on your calculator (STAT CALC followed by
any choice except for 1 or 2), the special list called RESID is recomputed
for you. Beware that if you need the values in the RESID list, you should
save them to another list beforehand, since they will be “clobbered” the next
time you perform a regression.
Since residuals are a type of “error” in estimation, the entries in the RESID
list are computed according to the error formula we discussed earlier in the
year: actual minus predicted. In other words, 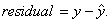 For linear
regression, this is the same as the formula your book gives at the top of p.
222. However, note that a residual can be defined for any type of regression, not merely linear regression. The formula
is always the same for any type of regression: For linear
regression, this is the same as the formula your book gives at the top of p.
222. However, note that a residual can be defined for any type of regression, not merely linear regression. The formula
is always the same for any type of regression: 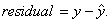
The general process of finding a curve (i.e., mathematical model) to fit a
set of data points in a scatterplot is called curve fitting. The most common type of curve fitting is linear
regression (STAT CALC 8), and in fact if you get an MBA you will seldom do
any other type of curve fitting. The “curve” in this case would simply be a
straight line, which is called the least-squares regression line or LSRL for
short. The term “least squares” refers to the fact that the LSRL is the
unique line that minimizes the sum of the squared residuals.
If you understand the definition of residual as “actual minus predicted” or
“observed minus expected,” you should understand why we say that a positive residual indicates a data
value that is above the curve, while a negative
residual indicates a data value that is below the curve. Being above the
curve, after all, means that y is
greater than 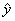 , which means that the residual, namely , which means that the residual, namely 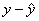 , is positive. By contrast, being below the curve means
that y is less than , is positive. By contrast, being below the curve means
that y is less than 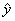 , which would make , which would make 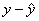 be negative. be negative.
In any LSRL, the sum of the residuals must always equal 0. This fact can be
proved mathematically, though the proof is beyond the scope of our course.
Note that there are other types of linear regression for which the residuals
do not necessarily add up to 0, and in nonlinear regression
(quadratic, exponential, sinusoidal, etc.), the residuals almost never add up
to 0.
You could, if you had to, use the residual formula to compute the residuals
one by one and store them into a list for plotting on a scatterplot. You
could, but we never do, since that would be a waste of time. Instead, we
typically create the residuals at the same time we perform a linear
regression. The keystrokes are
STAT CALC 8 L1,L2,Y1 ENTER
2nd STAT PLOT ENTER
Choose “On” and choose the first icon (indicating a scatterplot chart type).
Set Xlist to L1 and Ylist to RESID.
Finally, press ZOOM 9 and copy the dots (reasonably accurately) onto your
paper.
Important: After plotting your points, press the WINDOW key so that you can
tell what the bounds of your graph are in the x and y directions.
Label each axis (both x and y) with the following pieces of
information:
1. At least 2 numeric values (min. and max. will suffice)
2. Name of variable
3. Units in parentheses.
For example, in a graph of height as a function of shoe size, you would label
your x-axis with values from, say,
6 to 14, plus the following words:
Shoe Size (adult male units, U.S.)
You would then label the y-axis
with values from, say, 55 to 84, plus the following words:
Height (inches)
As you remember from precalculus, a residual plot that shows a random pattern
with no “flaring” left to right is desirable. Such a random pattern would
suggest that the regression fit you found is an appropriate fit to the data,
especially if the r2
value is close to 1 and the absolute size of the residuals is small.
A residual plot that shows a bowl-shaped, dome-shaped, or wavy pattern is
considered bad. These are all indications that your regression model is inappropriate.
The most common boo-boo is to use a linear regression when a power or
exponential fit would be more appropriate. You may have a high r2 value if you do this,
but it doesn’t matter! You will still be marked down by the AP graders, since
the residual plot would have a strong bowl-shaped look to it.
[This is the origin, by the way, of the famous catch phrase invented by
Eduard Ferrer: “That’s BOWL-SHAPED, Mr. Hansen!”]
|
|
|
F 10/15/010
|
Test (100 pts.) on all material covered so far this year
(through p. 217, plus the first tan box on p. 228), except for “Quick Study”
readings and the radio broadcast.
|
|
|
M 10/18/010
|
HW due at start of class:
Re-do your entire test from last Friday,
including all parts of #12 and #13, and record how long it takes you. You may
confer with other students if you wish, but the learning benefit is greater
if you push yourself to do the best possible job on your own before you break
down and call somebody or look in the textbook. The test may be re-graded for
accuracy as a double (or triple) homework assignment. Grammar, neatness, and
legibility count.
Also, group leaders must submit
final versions of group project methodology statements today. (These can be
turned in after school if necessary, but no later than 3:15 p.m.) You are
welcome to get started earlier on data gathering if you have verbal approval
from Mr. Hansen.
Groups:
Justin, Nick S., Andrei, Edward (sport vs. satisfaction)
Jordan, Dominique, Julien (personality impressions related to height)
Tip, Ousmane, Preston (original topic nixed; replacement TBD)
Brennan, Jamie, Zeke (political leanings by ZIP code)
Chick, Alex, Nick R. (workload and math grade by school)
Andrew, Phineas, Daniel (bag-lugging weight vs. STA form)
|
|
|
T 10/19/010
|
HW due: Read pp. 238-252
and work on group project.
|
|
|
W 10/20/010
|
HW due: Rework your test
from last week, especially all three
parts of the question regarding randomization, replication, and control.
I saw many wrong answers when I spot-checked.
|
|
|
Th 10/21/010
|
HW due: Write p. 253 #5.54.
Also, prepare for another “Quick Study” quiz from the Monday,
October 18, article that appeared in The
Washington Post.
|
|
|
F 10/22/010
|
HW due: Write p. 253 #5.55
(companion problem to yesterday’s assignment) and work on group project. Both
#5.54 and #5.55 are likely to be collected and/or spot-checked.
|
|
|
M 10/25/010
|
HW due: Before starting the
take-home test, read pp. 221-227. There is no new material here, and all of
the terminology (residual, residual plot, influential observation, etc.) has
been covered in class, but you may find the textbook reading to be helpful as
you prepare to take the test. Take some reading notes, as always.
Take-Home
Test (20 pts.) is due at start of class. Click the link at left to
view the test, and print it out. Before starting, make sure you have done all
the textbook reading (including the assignment immediately above), and treat
the test like an in-class test. The only way you will get better at taking
tests is by practicing. Taking the test with your textbook or notes open is
not a good assessment of what you have learned, since you will not fully come
to “know what you don’t know” (metaknowledge).
Find a clear work area where you will not be disturbed for at least 50
minutes. Your calculator is permitted, as always, but you should take the
test without using any notes. Record your time in the upper right corner of
the first page, in the space provided.
After you have finished the test, you may extend and revise your answers if
you wish. Use a different color of pencil (or a pen) for this purpose. I will
permit you to work together if you wish, but as I have explained repeatedly
in class, outright copying or
paraphrasing is prohibited and may be treated as an honor violation.
|
|
|
T 10/26/010
|
HW due: Work on group project.
Leaders may be required to give another update today.
|
|
|
W 10/27/010
|
HW due: Work on group
projects, and prepare for the Quick
Study quiz.
|
|
|
Th 10/28/010
|
HW due: Make sure you are
still prepared for yesterday’s quiz, and work on your group projects.
In class: Work on the following “Excelcise” (Excel exercise). There is a time
limit of 5 minutes, and everyone must eventually pass. My best time, with
practice, is 2:10. It is unlikely that anyone will pass on the first day, but
who knows? Anyone who is proficient at text messaging should be able, at
least in theory, to learn these steps. Mouse usage is permitted, but you will
find that the less you use your mouse, the less time you will waste.
1. Begin a new workbook in Excel (File / New, or Ctrl+N if you
are in a real hurry).
2. Enter the following four headings in row 1, columns A through D:
SubjectID NumSiblings NumLivingGrandparents NumExGirlfriends
3. Make row 1 bold, not only for the four existing entries, but also for any
future column headings in row 1.
4. Freeze the worksheet panes so that row 1 and column 1 will always be
visible. (Place cursor in cell B2 and issue the Worksheet / Freeze
Panes command, or Alt+W F. Note that if you accidentally put your cursor in
cell A2 instead of B2, freezing the panes will freeze row 1 but no columns.)
5. Place the numbers 1 through 4952 in cells A2 through A4953. Leave these
values as values, not as formulas.
6. Directly underneath the subject numbers, type the following in rows 4954
through 4965, leaving row 4961 blank:
mean
s.d.
min
Q1
median
Q3
max
Correlations (r values)
NumSiblings
NumLivingGrandparents
NumExGirlfriends
7. Apply bold formatting to rows 4954 through 4965.
8. Highlight columns A-D, and use Format / Column / Autofit
Selection (Alt+O C A) to widen them appropriately.
9. Fill cells B2 through D4953 with random integers between 0 and 4,
inclusive. The formula is
=INT(RAND()*5)
10. Replace cells B2 through D4953 with their values. (Keystrokes: Ctrl+C,
Alt+E S V Enter.)
11. Create suitable formulas in cells B4954 through D4960. Hint: Do column B first, then copy to
the right.
12. Create named ranges from the names in cells B1 through D1. (Keystrokes:
Ctrl+Home, UpArrow, highlight B1 through D1, Shift+Ctrl+DownArrow, press
UpArrow 7 times while still holding Shift, Alt+I N C Enter.)
13. Create suitable correlation formulas in cells B4963 through D4965. You
can make one formula in cell B4963 and then copy it:
=CORREL(INDIRECT($A4963),INDIRECT(B$1))
14. As a check on your work, observe that the five-number summaries for all
three data columns are 0,1,2,3,4. Also observe that the sample means are all
close to 2, and the sample standard deviations are all close to 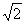 . Finally, observe that the correlations are 1 for each
column when paired with itself, but the correlations are all close to 0 when
each column is paired with a different column. Correlations have the same
value regardless of the order in which the columns are specified. . Finally, observe that the correlations are 1 for each
column when paired with itself, but the correlations are all close to 0 when
each column is paired with a different column. Correlations have the same
value regardless of the order in which the columns are specified.
|
|
|
F 10/29/010
|
End of Q1. All Mathcross puzzles, group projects, and
any other graded items must be submitted by 3:00 p.m. today.
|
|