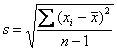|
W 9/8/010
|
First day of class. Do
not write in your textbook. Please return it immediately to Ms. Ulasevich in
the bookstore. She has ordered the correct
textbook by Peck, Olsen, and Devore (the vendor made an error) and will
have a replacement for you in about a week. We will do non-textbook
assignments in the meantime.
|
|
|
Th 9/9/010
|
HW due: Watch video
topic #3B (Greek alphabet for statistics) and the quiz-prep material
below.
There will be two 10-point quizzes.
The first will be on the Greek alphabet, and the second will be based on
yesterday’s class discussion. Here are the questions for the second quiz,
with answers in italics (bracketed portions are optional).
1. What is mathematics? [The science of abstraction:] the study of
patterns.
2. Are data plural? Yes, always.
3. What are data? Facts that are either categorical or
quantitative.
4. What is statistics? The study of data [often considered to be
a branch of applied mathematics, though increasingly seen as a separate
field].
5. What is a statistic? A number computed from data.
6. What is a parameter? A number that describes a population.
[Also, in mathematics, economics, engineering, game theory, and many other
fields, the term “parameter” often means an adjustable constant.]
7. What is our course
about? Variability.
8. Say more . . . We
use statistics to estimate parameters. Knowing how variable a statistic is allows us to say how confident
we are about our estimate. [Point estimates are for sissies.]
9. What is a distribution? The set of all possible quantitative
outcomes. [Note: We never use the word “distribution” when referring to
categorical data. Categorical data are often depicted with bar graphs, a
topic that you probably understood fully before you were a teenager.
Quantitative data require histograms, not bar graphs.]
10. What are some common
ways of depicting distributions?
Boxplot, modified boxplot, stemplot, histogram, [and perhaps most useful of
all, the relative frequency histogram, in which the probabilities are shown
adding up to 1].
11. So how is it that we
could use a statistic to estimate a parameter? We consider the “DOAPS”: the hypothetical distribution of
all possibilities for a statistic. [If the DOAPS has
high variability, we cannot estimate the parameter very accurately, but if
the DOAPS has low variability, we can estimate the parameter within a narrow
confidence interval.]
[Bonus Question #12. Do we
ever know exactly what the “DOAPS” looks like? No, and that is the hardest thing about our subject. It takes most
people several months to get comfortable with the concept. People who have
never studied statistics have no clue. The technical name for DOAPS is
“sampling distribution,” and that is the term you should use on your AP exam.
Most people can understand the term “distribution,” because a distribution is
easy to understand from looking at a histogram, but the term “sampling
distribution” is tricky. The distinction is that in a sampling distribution,
the quantities in the distribution are statistics instead of data
values.]
|
|
|
F 9/10/010
|
HW due:
1. Watch the Simpson’s Paradox video
and take some notes. Reading notes will be graded. They may be brief and
cryptic, but you must have some notes of your own. For full credit, follow
the formatting requirements.
2. Read Mr. Hansen’s absence and tardiness policies.
A quiz is possible either today or next week.
|
|
|
M 9/13/010
|
Quiz (10 pts.) on last Friday’s video. A second
quiz on the absence and tardiness policies is likely.
HW due:
1. Read the following paragraphs:
We use the lower case letter s to
denote standard deviation as a statistic,
and we use 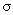 (lower case sigma)
to denote standard deviation as a parameter.
This convention of using Roman letters for statistics and Greek letters for
parameters is common in our subject, though there are a few exceptions. (lower case sigma)
to denote standard deviation as a parameter.
This convention of using Roman letters for statistics and Greek letters for
parameters is common in our subject, though there are a few exceptions.
The formula for s, which you will
never need to memorize, is 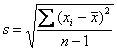 , where n = number
of data values. Your calculator computes s
for you. , where n = number
of data values. Your calculator computes s
for you.
We will always ignore the value that the calculator gives for 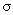 , with one exception that we will encounter in a few
months. However, for all practical purposes, you can say that you will ignore
the value of , with one exception that we will encounter in a few
months. However, for all practical purposes, you can say that you will ignore
the value of 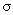 shown by the
calculator. shown by the
calculator.
The calculator does not have the ability to show a lower case s with a subscript of x. Therefore, your calculator shows
standard deviation as Sx. However, you will never write it that way. Always
write it as s.
2. Write out the answers to the following questions concerning Bill Bulldog’s
morning commuting times over the course of 2 weeks, which were as follows (in
minutes):
14, 17, 14, 15.5, 15, 15, 19, 14, 15, 18
(a) Sketch a histogram, a stemplot, and a boxplot of these data. You
supposedly learned all of these in previous classes. If you have forgotten
what the terms mean, look them up online.
(b) Compute the mean, mode, and median of the data. Use the notation 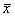 to label your mean,
the notation Q2 to label
your median, and the word “mode” to label your mode. Again, you were taught
the terms mean, mode, and median in previous classes. to label your mean,
the notation Q2 to label
your median, and the word “mode” to label your mode. Again, you were taught
the terms mean, mode, and median in previous classes.
(c) Use the technique demonstrated in class on Friday to compute s. No work is required, but give your
answer in the following format:
s = _____ minutes
|
|
|
T 9/14/010
|
HW due: Prepare for the
quiz that was supposed to occur yesterday. Then answer the question below.
1. Throckmorton’s 11 closest friends have the following heights:
5'2", 5'7", 5'9", 5'10", 5'10", 5'10",
6'0", 6'0", 6'2", 6'4", 7'2".
(a) Convert all values to inches, and make a histogram and a boxplot.
(b) Use the STAT CALC L1 ENTER technique that we learned last
Friday to compute the min., the first quartile, the median, the third
quartile, and the max. (Scroll your display with the down-arrow to see all
five values.) These five values are called the five-number summary of the data. Write the five-number summary.
(c) The IQR (interquartile range) equals Q3 − Q1.
Compute the IQR for this data set.
(d) In class on Monday, we defined an outlier
to be any value that is more than (1.5 · IQR) above Q3 or more
than (1.5 · IQR) below Q1. Write one or two sentences to explain
clearly why Throckmorton’s shortest friend is not an outlier, but his tallest
friend is. Be clear and specific. (Don’t write something bland and vague
like, “The 62-inch friend does not meet the definition of outlier, but the
86-inch friend does.” Instead, explain exactly why the definition is or is
not satisfied, using specific numbers.)
(e) Based on your judgment of the histogram and/or boxplot, do these data
exhibit skewness? (Either “yes” or “no” will be accepted as an answer. You
must explain your reasoning.)
(f) One rough measure of skewness is the difference between the median and
the mean. How close are the median and the mean in this example? Show your
work, and be sure to use correct notation (symbols, that is) when referring
to the median and mean.
(g) Occasionally we may find it useful to compute the trimmed mean, which is the mean after removing any outliers.
Compute the trimmed mean for this data set, and write a sentence or two to assess
whether or not the trimmed mean gives a truer sense of the central tendency
of the data set than 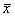 does. does.
|
|
|
W 9/15/010
|
HW due:
1. Since we are still waiting for our textbooks to arrive, let’s all listen
to Monday night’s 60-minute-long radio program (scroll to the bottom of
the page to see the audio link) or, if you are in a hurry, read
the transcript. The program itself is better than the transcript, in my
opinion, since it gives a good feeling for the central role that statistics
will play in U.S. educational reform. Also, make sure you are ready for
possible quizzes on both this radio program and last week’s video. Both
quizzes will be “open notes.”
2. Today and every Wednesday until December, there is a recurring assignment
to read the “Quick Study” segments in The
Washington Post. These segments, and there are usually three of them each
week, give a brief glimpse of statistics as used in the field of medical
research. If you do not receive a newspaper at home, or if you are unable to
read the copy in the STA Ellison Library, here is a link to the most
recent online version (sometimes the article is omitted in the print
edition for space reasons). The date of this article is 9/7/2010, and this
time there is only one segment instead of the usual three. Again, your quiz
on this material will be “open notes.”
|
|
|
Th 9/16/010
|
HW due:
1. Be ready for a possible quiz on the Post “Quick Study” article.
2. Below are the aggregate quiz results for students who have taken all four
10-point quizzes.
26, 30.5, 32, 32, 33, 33.5, 34, 34.5, 34.5, 35.5, 36, 37.5, 38, 39, 40
(a) Make a histogram, a boxplot, and a stemplot for these data.
(b) Compute the median, standard deviation, and five-number summary for the
data. Use proper notation.
(c) One measure of skewness is the direction in which the mean deviates from
the median. If the mean is pulled lower
than the median (by a long left tail of the distribution), we say that the
distribution is skew left. If the mean is pulled higher than the median (by a long right tail), we say that the
distribution is skew right. Show that this distribution has little skewness
by this measure.
(d) Another way of gauging skewness is to look at the boxplot and see which
tail is longer. By this measure, in what direction does the skewness lie?
3. Below are Mr. Hansen’s morning commuting data for the first half of
September. All times are in military format (HHMM) to the nearest half
minute.
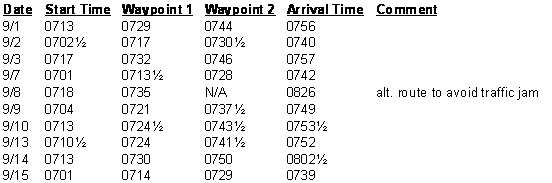
(a) Explain why it is not possible to work with the data in their current
format, not even if the fractions are converted to decimal values (for
example, coding the start time for 9/2 as 702.5). Hint: Look at all of the data.
(b) What would you recommend as a standard method of “coding” the data for
use in statistics and graphs? Many correct answers are possible.
(c) If we are looking for patterns in the data, what should we do with
anomalous data or missing data values? (See, for example, the data for 9/8.)
Explain your reasoning.
(d) Look for patterns in the data. List two or three interesting patterns that you observe. (No, the fact that Mr.
Hansen nearly always takes the same route to work is not interesting.)
(e) Carefully describe several statistics that would help us find interesting
patterns in the data. Try to go beyond the obvious ones (mean, median,
standard deviation, IQR), though you are certainly free to use some of those
if you wish. Don’t simply say “mean,” though, since that is vague. Mean of
what?
|
|
|
F 9/17/010
|
Catch-up day (no additional
HW due; use the time to get caught up). A quiz on recent class discussions is
likely.
|
|
|
M 9/20/010
|
HW due: Consider the
updated commuting data below, and answer the questions that follow.

1. Code the start times as “minutes after 0600.” For example, the first entry
would be 73, and the last entry would be 49. Record your column of data on
your paper and in your calculator’s L1 list.
2. Code the arrival times in the same manner. The first entry would be 116,
and the last entry would be 84. Record your column of data on your paper and
in your calculator’s L2 list.
3. Compute the elapsed times by punching L2 − L1
STO L3 ENTER. Record the values from column L3 on your
paper so that you have a convenient record of them.
4. Plot a scatterplot (i.e., xy-plot)
having L1 on the x-axis
and L3 on the y-axis.
You learned how to do this in precal. [If you have forgotten the steps, they
begin with 2nd STATPLOT ENTER On. Then highlight the first pictograph, the
one that looks like a tiny scatterplot, press ENTER, set Xlist to L1,
set Ylist to L3, set Mark to the square, and press ZOOM 9.]
5. Record a rough sketch of your scatterplot on your homework paper. Plot all
12 ordered pairs. (You can plot them as dots to save time.) As for the axes,
your required minimum labeling is at least 2 x-values, at least 2 y-values,
description of each variable (in this case, “departure time” for the x-axis and “elapsed time” for the y-axis), and the units (in
parentheses). Thus the x-axis should
be labeled with at least two values (the min. and max. will suffice) and the
following label:
Departure Time (minutes after 0600)
Similarly, the y-axis should be
labeled with at least two values (again, the min. and max. will suffice) and
the following label:
Elapsed Time (minutes)
6. Make sure that your calculator’s diagnostics are turned on. You will want
to leave them turned on throughout the entire school year. (If you buy a new
calculator, or if you change the backup battery on your calculator, you need
to remember to re-enable diagnostics.) The keystrokes for the DiagnosticOn
command are as follows:
2nd
CATALOG (the 2nd function of the 0 key)
D (the x−1 key;
note that the alpha lock is automatically enabled for you)
(now press the down-arrow key about 8 times to highlight DiagnosticOn)
ENTER
ENTER
7. Perform a linear regression of L3 upon L1, and write
down the linear correlation coefficient, r.
[Again, you learned this skill in precal, but if you have forgotten the
steps, here they are: STAT CALC 8 L1, L3,Y1
ENTER. The commas are required, and the way you get Y1 is by using
VARS Y-VARS Function Y1.]
8. Press ZOOM 9 to see the linear regression line overlaid on your
scatterplot. Add this regression line to the scatterplot sketch you made in
exercise 5 above.
9. Mr. Hansen believes that the later he leaves for STA in the morning, the
longer the trip takes. Do Mr. Hansen’s data prove this claim? Do they
corroborate this claim? Do they refute this claim? Explain your answer
briefly.
In class: Watch and discuss Dr.
Hans Rosling’s TED video.
|
|
|
T 9/21/010
|
HW due:
1. Pick up your textbook at the bookstore between 3:00 and 3:30 on Monday. If
you are unable to do this before the bookstore closes at 3:30, then come in
early Tuesday morning to do your reading in the Math Lab. (I will have one or
two books you can borrow.)
2. Read pp. 1-19 for review purposes. Reading notes are required, as always,
but you can zip efficiently through this reading. For example, most of pp.
2-3 can be scanned quickly, since the examples, while somewhat interesting,
do not contain anything you would be expected to remember. The bottom of p. 3
is much more important and should be read carefully. Pay special attention to
definitions, tan and green boxes, and section subheadings. There are a few
new terms sprinkled here and there (for example, in the middle of p. 14) that
you are responsible for knowing. An open-notes quiz is possible.
3. Several students did not finish their HW that was due yesterday. If you
are one of those people (e.g., if you failed to compute r or failed to plot the regression line overlaid on your
scatterplot), you are expected to make those additions. The assignment may be
picked up and graded a second time.
|
|
|
W 9/22/010
|
HW due: Prepare for a quiz
on last
week’s Quick Study, as well as this
week’s Quick Study. There is only one capsule article for each week. Also
read pp. 27-46 in your textbook (through the bottom of the shaded box).
|
|
|
Th 9/23/010
|
HW due: Read pp. 46
(middle)-49, 51-54, 61-63; write p. 67 #2.58, 2.60.
|
|
|
F 9/24/010
|
HW due: Read pp. 75-83,
87-92, 97-104 (top); write p. 116 #3.29.
|
|
|
M 9/27/010
|
HW due: Read pp. 104-113, 117-124
(top), 127-130; write p. 138 #3.56. If you have some extra time, you may wish
to look at an actual Mr. Hansen test
from 2008. This year, if I were to recycle portions of the test (as is
likely), I would add some questions on Simpson’s Paradox, animated
scatterplots, and educational reform. Since we have not yet studied z scores and normal quantile plots, I
would also delete the following questions from the sample test:
8(b)
10 [the answer is z]
11(b)
12(b)
13
|
|
|
T 9/28/010
|
Test (100 pts.) on all material so far, except for
the “Quick Study” articles. Note
that anything discussed in class, including the technical meaning of error, the meaning of acronyms in the
news such as IRB and VAA, and the whimsical but quite useful regression rule 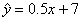 , are fair game for the test. You can earn a good score by
paying attention in class, but to get an A+, you will also need to review and
reflect upon your class notes. , are fair game for the test. You can earn a good score by
paying attention in class, but to get an A+, you will also need to review and
reflect upon your class notes.
|
|
|
W 9/29/010
|
No additional HW due, but
older assignments may be spot-checked. The “Quick Study” quiz that would
normally occur today has been postponed to tomorrow so that you have a day
off after your test.
|
|
|
Th 9/30/010
|
HW due: Read pp. 147-156;
change all occurrences of p to 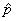 in the tan box on p.
155; write p. 157 #4.6, p. 159 #4.10, and the required reading notes below. in the tan box on p.
155; write p. 157 #4.6, p. 159 #4.10, and the required reading notes below.
[Copy this paragraph and the table below it into your reading notes. The
paragraphs after the table are optional.]
Notation: Our textbook uses p for sample proportion and 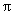 for population
proportion (i.e., probability). This is consistent with the general rule that
Roman letters are for statistics and Greek letters are for parameters. Many other
textbooks follow this convention. However, the AP exam uses for population
proportion (i.e., probability). This is consistent with the general rule that
Roman letters are for statistics and Greek letters are for parameters. Many other
textbooks follow this convention. However, the AP exam uses 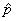 , not p, to
denote the sample proportion, and p,
not , not p, to
denote the sample proportion, and p,
not 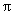 , to denote probability. To make matters even more
confusing, the same letter is used for a completely different purpose in the
second half of the course. Here is a handy translation table: , to denote probability. To make matters even more
confusing, the same letter is used for a completely different purpose in the
second half of the course. Here is a handy translation table:
|
|
|
|
|
sample proportion
|
population proportion (probability)
|
P-value of
a statistical test (second semester only)
|
|
|
|
many college-level texts
|
lower case p
|
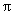
|
lower case p
|
|
|
|
our textbook
|
lower case p
|
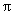
|
capital P
|
|
|
|
TI-83/84 calculators
|
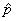
|
lower case p
|
lower case p
|
|
|
|
what Mr. Hansen wants
|
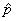
|
lower case p
|
capital P
|
|
|
|
AP exam
|
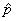
|
lower case p
|
capital P
|
|
|
|
[Optional additional notes.] The only notation that everyone seems to agree
on is the way to indicate the probability that a named event (such as event
A) occurs. That is universally shown as P(A), using a capital letter P and parentheses surrounding the
letter of the event.
For example, if we wish to compute the probability of getting a king and an
ace, in that order, when 2 cards are drawn without replacement from a
well-shuffled deck, the answer would be
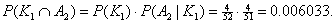
The vertical bar symbol, | , is read as “given.” Note that 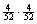 would give the wrong
answer, since we were told that the cards are drawn without replacement. would give the wrong
answer, since we were told that the cards are drawn without replacement.
In class: Surprise visit from 14-year-old Davidson Fellow, Meredith Lehmann
of La Jolla, California.
|
|