MODD / Mr. Hansen 10/15/2010

Name: __________KEY__________

General Instructions: Raise your hand if you have a question. Write answers in the space provided. If you need additional room, write "OVER" and use reverse side.

Part I: Essay.

1.	Explain, in general terms, how undersampling of a digital image can lead to “banding” patterns. What are these bands called?
	They are called Moiré patterns.
	When two grids are overlaid at an angle or have slightly different mesh sizes (and NOTE! this is exactly the situation we have when a digital photo is sampled at too low a resolution), the lack of information causes some lines to be perceived as if their pixels belong to other lines or curves. Example: lane reflectors on the Beltway.
2.	State Nyquist’s Theorem (the “sampling theorem”) in general terms. Exact precision is not required, since it is a fairly difficult theorem. Come as close as you can.
	The rate at which a signal must be sampled in order to avoid aliasing artifacts is at least TWICE the highest frequency found in the original signal source.
3.	State one advantage that two’s complement representations have over one’s complement.
	The wraparound point for two’s complement is in a more sensible place, and there is only one representation for 0 in two’s complement.

Part II. Computation. Please show adequate work. After you have computed an answer for all the questions, you may use Mr. Hansen’s computer to check your answers.

4.	Convert the following bitstream to (a) big-endian hex and (b) little-endian hex using 16-bit words: 0100 1010 1010 1111 0101 0101 0101 0011 0101 0101 0101 1010 0101 0110 1010 0000
(a)	4A AF 55 53 55 5A 56 A0
(b)	AF 4A 53 55 5A 55 A0 56
5.	Perform the following additions in hex:  11 0BBF +288 ==== 0E47 111 0818 +EEE ==== 1706 Note: This is 1706h, not 1706 decimal.                The decimal value is 1(4096) + 7(256) + 0(16) + 6 = 5894.
6.	Perform the following hex subtractions using two’s complement arithmetic, showing enough work so that it is clear that you know what you are doing. You may check your answer using borrowing and regrouping, of course. If your answer represents a negative number, be sure to indicate that. Then reinterpret your final answer as a decimal number using conventional human notation.
	0415        Rewrite as 0415        Rewrite as 0415 −6E7                  −06E7                  +F919 ====                  =====                  =====                                               FD2E
	The answer, FD2Eh, must be reinterpreted as a negative number since 6E7h > 415h. Thus we must take the two’s complement of FD2Eh, namely 02D2h = 0(4096) + 2(256) + 13(16) + 2 = 722 interpreted as a negative. Final answer: −722 decimal.
	1 03CC        Rewrite as 03CC        Rewrite as 03CC −2FB                  −02FB                  +FD05 ====                  =====                  =====                                              100D1
	We must subtract 10000h by discarding the lead digit, since we effectively added an extra 10000h when we rewrote the subtraction as an addition involving two’s complement. That leaves us with 00D1h, which equals 13(16) + 1(1) = 209 decimal.

Part III. Bits, Bytes, Hex, Hertz, and Moore’s Law

7.	Suppose that a certain computer capability costs me $1000 to acquire today. Approximately how far in the future will it be before I can acquire the same hardware capability for about $1? Show your work, and write a sentence or two.
	Short version: 1000 means about 10 doublings. Assuming the “two year” version of Moore’s Law is true, we will need approximately 10(2) = 20 years.
8.	In our class, we define a kilobyte to be ___1024___ bytes or ___8192___ bits.
9.	How many megabytes are in a terabyte? Give both an approximate answer and an exact answer. Exponential notation is acceptable.
	Approximate answer (preferred): Since K, M, G, T have a factor of about 1000 for each step, and since M to T is 2 steps, we need approximately a thousand thousand MB for 1 TB, or about 1 million.
	Exact answer: MB = 2^20 bytes = 1,048,576 bytes
	TB = 2^40 bytes = 1,099,511,627,776 bytes
	Divide to get 1,048,576 MB in a TB. Easier method: Use skills from Algebra II to get .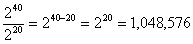
10.	Mr. Hansen’s old antique laptops have a clock speed of about 2.5 MHz. Modern computers are generally between 2 and 3 GHz in their clock speed. How much faster is this (to the nearest order of magnitude)? [“Order of magnitude” refers to powers of 10.]
	About 10^3 or 1000. [You are supposed to do this in your head; no work is expected.]
11.	What do we mean when we say that a modern computer runs at, say, 3 GHz? What are we talking about, in plain English? 3 billion clock cycles per second

12.	I wish to perform digital audio sampling of a 3-minute song using 2-channel stereo, a bit depth of 16 bits per sample, and a sampling rate of 44.1 KHz. Compute the data requirement (uncompressed). Show work.
	3 minutes · 60 sec/min. · 2 bytes/sample · 44100 samples/sec = 15,876,000 bytes
	However, we must double this, since there are 2 channels. Final answer: about 30 MB.
13.	How many different colors can be represented with a bit depth of 8 bpp for digital imaging?
	2^8 = 256
14.	Unless the palette is carefully optimized in #13 to choose the “best” colors for the image, the image will almost certainly exhibit what artifact? __posterization__

15.	Does a higher resolution (megapixel count) help to solve the problem in #14? Why or why not?
	No, since higher resolution addresses only how closely spaced the pixels are, not the issue of how many unique colors are available.
16.	Explain, in general terms, how it is possible for a car wheel in a TV advertisement to appear to be stationary (or even turning backwards!) when the ad is shot at 30 frames per second. Diagrams may be helpful.
	If the wheel is turning at 30 revolutions per second, then each frame will show the wheel as having made one full turn, which to an observer creates the illusion that the wheel is not moving at all. [The same is true, by the way, if the wheel has 5 spokes and is turning at 6 revolutions per second, since 30 “spoke passings” will occur per second, and with a frame rate of 30 frames/sec., each frame will look exactly like the frame before it, giving the illusion of no motion.]
	With a little arithmetic, we can easily show that a 5-spoke wheel rotating at 0, 6, 12, 18, 24, 30, or 36 rotations per second will all have exactly the same appearance, namely the illusion of no motion.
	The illusion of backward motion is created when during each 1/30 sec. time interval, a spoke passes almost all the way, but not quite, to the position of the previous spoke. The viewer then perceives that apparent motion, which is in the direction opposite to the actual motion, as being the continuous motion of the wheel.

17.	Make a circuit diagram fragment to show the concept of (~A) NAND (~B). Then give a truth table proof to show that (~A) NAND (~B) is equivalent to A OR B.
	A	B	~A	~B		~(), same as ~A NAND ~B
	___	___	___	___	________	________________________________
	1	1	0	0	0	1
	1	0	0	1	0	1
	0	1	1	0	0	1
	0	0	1	1	1	0
	Observe that the final column has the exact same pattern (1, 1, 1, 0) that we would see with an OR gate for A OR B. (Q.E.D.)