|
W 9/8/010
|
First day of class: Bits,
bytes, hex, and hertz. (Introduction and basic terminology; discussion of
desired topics to be covered during the semester.)
|
|
|
Th 9/9/010
|
HW due: Your assignment is to
order the Engineering Our Digital
Future textbook (ISBN
0-13-184828-3 or 9780131848283) from Amazon.com or another source of your
choice. It is not economical for the STA bookstore to order 3 copies, and you
can save a significant amount of money by buying your own copy on-line.
Prices vary widely, from a low of about $40 to a high of more than $160. Let
me know your ordering status when we meet in class.
There are two ISBN formats in common usage. You can search for the book
either by its ISBN-10 code, which is 0-13-184828-3, or by its ISBN-13 code,
which is 9780131848283.
Also, review in your mind what we did yesterday. We need to know our hex
digits from 0 through F. I will probably give you an ungraded quiz to make
sure you understand.
|
|
|
F 9/10/010
|
HW due:
1. Order your textbook if you have not already done so. The link is above.
2. Do the following in hex, showing your work. You can use the Windows Calculator
to check your answers, but be sure to show your work.
FAB
+BAC
CAB
—91F
FADE
+BFF
CCCC
–1D2
|
|
|
M 9/13/010
|
HW due:
1. Beginning this week, the following 3 pieces of equipment are expected
every day: pencil, 3-ring binder with filler paper, and textbook (as soon as
yours arrives in the mail, that is). Please purchase a 3-ring binder over the
weekend if necessary. I also have a few in my office that are for sale cheap.
2. Answer the questions below on a separate sheet of paper.
According to Moore’s Law (one version, at least), computing power at a given
price point doubles approximately every 1.5 years. In the 35 years since I
entered high school, there have been about 23 doublings, since 35/1.5 is
approximately 23. That means that hard disk storage, RAM, nonvolatile RAM,
etc. are all about 223 times cheaper today than they were when I
was a high school student. We learned on Friday that 210 is about
a thousand, which means that 223 = 23+10+10 = (23)(210)(210)
= 23(1000)(1000) = roughly 8,000,000, which we round off to 10
million since 210 is actually a little more than 1000 anyway. As
we discussed, disk space has gone from about $1000 per MB in the mid-1970s to
about 10 cents per GB today.
(a) Verify, showing your work, that 10 cents per GB is indeed about 10
million times cheaper than $1000 per MB.
(b) Using the figure of 10 cents per GB for today’s price, estimate the
current cost of an exabyte of disk storage. Show your work. Is it practical
to have an exabyte of storage dedicated for a cell phone? [If you have
forgotten what an exabyte is, please look it up online.]
(c) When your children attend high school a generation from now,
approximately how much will an exabyte of long-term storage cost? Note: It won’t be disk storage, since disks
will surely be obsolete by then. However, use today’s disk storage cost that
you found in part (b) as a starting point. Indicate how many years you are
using in your assumptions, and show your work.
|
|
|
T 9/14/010
|
No additional HW due, but I
would like to see all of your existing assignments, organized and complete,
in one place. A 3-ring binder is required.
|
|
|
W 9/15/010
|
HW due:
1. Write the truth table for the NAND gate. NAND (an abbreviation for “not
and”) takes two inputs, which we can call A and B, “ands” them together, and
finally inverts the result. Thus the output is merely the negation (opposite) of 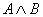 . .
2. The symbol for an AND gate is 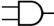 (2 inputs entering from the left, 1 output
exiting to the right), and the symbol for a NAND gate is almost identical
except for a circle on the right that indicates inversion of the output: (2 inputs entering from the left, 1 output
exiting to the right), and the symbol for a NAND gate is almost identical
except for a circle on the right that indicates inversion of the output: 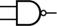 . Show
how it is possible to connect a group of 3 NANDs in some fashion so that,
altogether, their overall behavior is the same as . Show
how it is possible to connect a group of 3 NANDs in some fashion so that,
altogether, their overall behavior is the same as
(a) a single AND gate,
(b) a single OR gate.
The answers are on Wikipedia (of course, as almost everything is), but see if
you can solve these puzzles by working on your own. Maybe you will get some
ideas by observing how a NOT can be created from a NAND gate as follows:
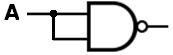
Observe, please, that if A = 1, then 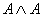 = 1, so that A NAND
A = 0, and if A = 0, then = 1, so that A NAND
A = 0, and if A = 0, then 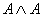 = 0, so that A NAND
A = 1. But either way, the output equals the negation of A. Therefore, this NAND
gate, with A driving both of the inputs, functions exactly like a NOT gate. = 0, so that A NAND
A = 1. But either way, the output equals the negation of A. Therefore, this NAND
gate, with A driving both of the inputs, functions exactly like a NOT gate.
|
|
|
Th 9/16/010
|
By your vote, Thursday is
our day off this week.
|
|
|
F 9/17/010
|
HW due:
1. Translate the binary serial bitstream 01001010101010111011101101011101
into
(a) little-endian hex using 2-byte words, and
(b) big-endian hex.
2. Use a truth table to prove that 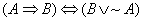 . The symbol “ . The symbol “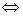 ” is found on the standard abbreviations page and means
“equivalent to.” In other words, show that the truth table pattern for ” is found on the standard abbreviations page and means
“equivalent to.” In other words, show that the truth table pattern for 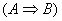 is exactly the same
as the truth table pattern for is exactly the same
as the truth table pattern for 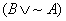 . .
3. The operations AND, OR, and NOT are sufficient to embody any logic that
computers and other digital devices can execute. We have seen how NANDs alone
can implement AND, OR, and NOT. Now, draw a diagram to prove that a logical
implication gate 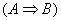 can be implemented
using NANDs alone. can be implemented
using NANDs alone.
4. Suppose that you wish to transmit 66 million copies of the integer value
255 to a friend. (This is a very boring message indeed.) Estimate how long
this transmission will take if you use a connection with a speed of 10
megabits per second. Document any assumptions you employ in your
calculations.
|
|
|
M 9/20/010
|
HW due: Review the table of
contents in your textbook, and read at least one chapter that appears
interesting. In class, we will discuss what you read and will develop a plan
for which chapters we will cover during the course of the semester.
Note: Reading notes are required.
Make notes as you read and/or record questions that you have for Mr. Hansen.
Follow the required formatting guidelines, and
save your notes in your 3-ring binder..
|
|
|
T 9/21/010
|
HW due: Read pp. 3-6, 7-11 (skip
exercises at top of p. 7), and 23-27; write p. 27 #1b or #1c (your choice).
|
|
|
W 9/22/010
|
HW due: Read pp. 105-125;
write p. 124 #7, 11. You can be creative in #11 (making up things that do not
yet exist is permitted).
|
|
|
Th 9/23/010
|
By your vote (a 2/3 vote
taken at 10 a.m.), today will be our day off this week.
|
|
|
F 9/24/010
|
HW due: Read pp. 125-135; write
pp. 142-143 #7-9, 15.
|
|
|
M 9/27/010
|
HW due: Reread your steganography handout and try to devise
a steganographic system for communicating digits embedded in normal speech. Write
up your ideas as a homework paper in standard format. There are no “right” or
“wrong” answers, but try to come up with something that you could actually
implement if you had to. For example, if you were a prisoner of war and were
put on TV for propaganda purposes, you might want to communicate a secret
message back to your friends in the U.S. (This actually occurred in 1966; you
can read about it here.)
|
|
|
T 9/28/010
|
HW due: Prepare for an oral
test over the material covered so far. Review your notes and your old HW
problems. If you do well, you will be exempt from taking a similar test to be
given for credit on Wednesday.
|
|
|
W 9/29/010
|
No additional HW due.
|
|
|
Th 9/30/010
|
No class today.
|
|
