|
M 4/4/011
|
No class.
|
|
|
T 4/5/011
|
No additional HW is due today.
|
|
|
W 4/6/011
|
HW due: Reread portions of Chapter 10 (as needed,
since it has been a long time), and write Exercises 10.1, 10.2, 10.7, and
short definitions of the terms shell
and shell script. Note that
Exercises 10.1 and 10.2 are on p. 123; the others are at the end of the
chapter.
|
|
|
Th 4/7/011
|
HW due: Complete yesterday’s assignment, especially
#10.2 (using the “ignore part of the interval and try again” approach). Then
read pp. 131-135 (through §11.4) and answer the question at the top of p.
135. In other words, draw the state diagram when card1 ==
card2 is true.
|
|
|
F 4/8/011
|
HW due: Read pp. 135-142 (to end of Chapter 11), and
correct Exercise 10.2 so that it can properly handle negative values for low and/or high. Test your
method with a variety of input values, until you are convinced that it meets
all the requirements and is bug-free.
The bug we found at the end of class yesterday was that a typecast to (int)
does not return the greatest integer less than or equal to randomDouble(low, high+1); instead, the typecast to (int) simply truncates the value, ignoring
the decimal portion.
There are two ways you can approach this. One is to use “if” logic, and
adjust the return value whenever the value you are about to return is
negative. The other approach is to use the Math.floor function before typecasting. If you choose the
second approach, which is cleaner, you may wish to read the online help for
the Math.floor function.
|
|
|
M 4/11/011
|
No class.
|
|
|
T 4/12/011
|
HW due: Read Chapter 12 (pp. 143-149); then do the
exercises below. Mr. Hansen will be available for help during D period on
Monday and also after school. Please come in for extra help!
1. Debug your randomInt method and test it so that you are sure it works
correctly. Mr. Hansen strongly recommends using the (int)Math.floor(randomDouble(low,high+1)) approach, using randomDouble as a helper method. However, you are free to
proceed as you wish. Chase and Matthew were the only students with a completely
correct version of randomInt as of last Friday. E-mail your corrected randomInt method to
Mr. Hansen over the weekend.
2. How many integers are there between −7 and 3, inclusive?
3. How many integers are there between any two integers m and n, inclusive,
assuming that n > m?
4. Write a new main method that creates and fills an array (called BigBadArray) with
random integers between −7 and 3, inclusive. Your BigBadArray should
consist of 2000 int values. You should, of course, call your previously
written method, randomInt.
5. Modify your main method from the previous step so that after
creating and filling BigBadArray, you use a loop to determine how many array entries
are equal to −7, −6, −5, and so on, all the way up to 3. It
is up to you whether to name your counters one by one (CountNeg7, CountNeg6, CountZero, CountPos1, etc.) or
to name them as part of another array. The second approach is cleaner and
requires less code, but the first approach is probably easier to implement.
Output the values of your counters so that you can see how many entries of
each value were generated.
6. If BigBadArray contains a true uniform distribution of random
integers, approximately how many entries would we expect to be counted by
each of the counters?
7. How closely did your output values conform to these expected counts? If
you re-run your program, do you achieve similar results?
|
|
|
W 4/13/011
|
Write Exercise 10.12 on p. 130 (pseudocode or
flowchart only; do not write Java
code) and Exercise 11.2 on p. 142 (Java code expected).
Can you think of any more doubloons? Here are some I came up with: kook,
poop, woowee.
|
|
|
Th 4/14/011
|
HW due: Read §§13.1-13.5 (pp. 153-156); write the 3
exercises below.
1. Write several additional comment lines for Nick’s code (reproduced below).
2. You can find a small bug if you compare the flowchart carefully with the
code. Correct the bug, and then test your revised isDoubloon method to verify
that the bug is fixed.
3. Explain the comment marked IMPORTANT below. Why might some programmers be
tempted to place the statement in the wrong place (for example, one line
farther up)? How does the flowchart guard against such a bug? Be specific.
public class NickDoubloon {
public static void main(String[]
args) {
System.out.println(isDoubloon("Shanghaiings"));
}
public static boolean
isDoubloon(String iword) {
int
i; //scratch loop counter
if
(iword.length() % 2 != 0) {
return false;
}
int[] counters=new int[26];
String
word=iword.toLowerCase(); //work with lower case version only
for
(i=0;i<word.length();i++) {
counters[(int)word.charAt(i)-97]++; //97 is ASCII
value for "a"
}
for
(i=0;i<26;i++) {
if
(counters[i]==1 || counters[i]>2) {
return false;
}
}
return true; //IMPORTANT!
This line must be outside the for-loop.
}
}
|
|
|
4/15/011
|
No additional HW due today. Whew! (Yes, it would
have been even better if this had been posted by 3:00 p.m. However, as you know,
there is a general rule that if HW is not posted by 3:00 p.m.—or by some
reasonable hour on Friday evening, before the weekend begins in earnest—then
there is no HW assignment.)
|
|
|
M 4/18/011
|
No class.
|
|
|
T 4/19/011
|
No class: Diversity Day in Trapier Theater, 10:00
a.m.
|
|
|
W 4/20/011
|
HW due:
1. Download Version
1.1.24 of the Python textbook, Think
Python: How to Think Like a Computer Scientist, and save the file to your
computer’s hard disk. You will notice that the author is the same as the
author of the Java text we used. The structure and some of the content are
strikingly similar between the two books.
2. Read pp. 1-26 of the new textbook, reading every word, even the sections
that are purely review for you. That which we do twice, we are more likely to
learn.
3. Pay special attention to the glossary pages at the end of each chapter
(hint, hint). Please note that the term “fruitful function” is not in common
usage in the world of computer science; it is merely an idiosyncratic term
that the book’s author invented. You should know the other terms in the
glossaries for Chapters 1-3, however.
4. Reading notes are required, as always.
5. Write an answer to the question posed in the middle of p. 14, in the final
sentence of §2.8: Can you think of a property that addition has that string
concatenation does not?
6. Write Exercise 2.3, #1-5, on p. 16. You may use a Python interpreter to
check your answers if you wish, but that is not required. We will postpone
the decision of which Python interpreter to use until later in the week.
7. Translate each of the following terms or symbols from Java into Python:
method
} // closing brace
//
8. Translate each of the following terms, symbols, or lines of code from
Python into Java:
function
: # colon character
x = len('mystring') # assume that variable x already
exists as an int
BigDash = '-' * 25
|
|
|
Th 4/21/011
|
HW due:
1. Read Chapter 5 (pp. 39-47) and make reading notes.
2. As you read, make two lists: Record as many similarities and as many differences
as you can find between Java and Python syntax.
3. Pay special attention to the glossaries at the ends of Chapters 1, 2, 3,
and 5 (hint, hint).
|
|
|
F 4/22/011
|
HW due:
1. Visit python.org and download Version
2.7.1 of the Windows x86 MSI Installer (or if you have a 64-bit machine, the
Windows x86-64 MSI Installer). Complete the installation on your computer.
2. Read Chapter 6 (pp. 51-60), paying special attention to the glossary at
the end (hint, hint).
3. Enter the factorial function code at the bottom of p. 58 and test your
function by calling it from the interpreter, as illustrated at the top of p.
59. What is the largest integer n
for which this function computes a correct value for n! (n factorial)?
|
|
|
M 4/25/011
|
No school.
|
|
|
T 4/26/011
|
HW due: Write Exercise 5.2 (pp. 47-48) and Exercise 6.6
(p. 61). Note that each of these exercises has 2 parts.
Mr. Hansen will be available for help by e-mail over the weekend, as well as
before school.
If you have additional time, you can earn some bonus points by completing the
pi-estimating exercise that Karl gave us in class last Friday. Remember, the
technique was that we would take
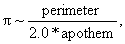
where the tilde symbol (~) is interpreted as “asymptotically equals.” We made
a loop in which the number of sides, n, would grow larger and larger. For
each iteration in the loop, we kept side length (which Karl called sl)
constant, and therefore the perimeter would be sl*n. We then used
trigonometry to find the apothem as a function of half the side length.
Interesting bonus questions:
1. Karl defined side length, which he called sl, as a constant floating-point
value, so that the perimeter would always be sl*n. Does accuracy of the pi
estimates get better or worse if we take the opposite approach, namely
defining perimeter as a constant floating-point value and computing sl by the
formula perimeter/n?
2. At a certain point, regardless of which method you use, accuracy starts to
break down, and you achieve little or no improvement in the pi estimates even
as you take larger and larger values for n. Why do you suppose this is? For
reference, the true value of pi is 3.14159 26535 89793 23846 26433 83279
50288 4197 . . .
|
|
|
W 4/27/011
|
HW due: Exercise 9.8 on p. 86. Use the technique
Karl taught us yesterday for checking for palindromes. For example, if x is a string, then x[::−1] will
be a reversed version of x. Check to see whether
x == x[::−1]
and you should be halfway home. (The hard part is in making substrings out of
partial bits of the numbers you are testing. The modulus operator should be
useful in that regard.)
Optional HW (for people who need more challenge, and you know who you are):
Answer bonus questions 1 and 2 from yesterday’s assignment. There are no
bonus points attached this time, but you can impress your ol’ teacher by showing
that you are interested enough to do a little extra analysis.
In class: Pop double quiz on recent Python vocabulary.
|
|
|
Th 4/28/011
|
HW due: Read Chapter 10 (pp. 89-100). Reading notes are
required, as always. As you do the reading, try the code snippets in the book
on your Python interpreter, and try other things as well so that you can
learn faster. For example, on p. 89, you see the code snippet
cheeses = ['Cheddar', 'Edam', 'Gouda']
If your hobby is cheese, like Wallace in the Wallace and Gromit movies, you
might find this example memorable or interesting. Everyone else, though,
would probably learn better with a more vivid example such as
favorite_sports = ['hockey', 'baseball', 'lacrosse']
|
|
|
F 4/29/011
|
HW due: Exercise 10.4 on p. 100.
|
|