|
T 2/1/011
|
HW due:
1. Read Chapter 2 (pp. 13-20). Reading notes are required, as always. A quiz over
the terms represented in the glossary at the end of the chapter is possible.
2. Also, follow the
link given near the middle of p. 17. On that web page, read §3.9
(Keywords) carefully, but skim quickly over the rest of the material.
Technical writing like this is hard to digest unless you limit yourself to
small doses. Answer the following questions in writing:
- You may have noticed that the writing style is
rather flat and lifeless. Why did the authors feel that it was necessary
to specify comments, keywords, identifiers, literals, separators, and
operators so precisely?
- In §3.10.5, is it really necessary to include
examples showing that literal strings within the same class in the same
package represent references to the same String object, that literal
strings within different classes in the same package represent references
to the same String object, that literal strings within different classes
in different packages represent references to the same String object,
that strings computed by constant expressions are computed at compile
time and then treated as if they were literals, that strings computed at
run time are newly created and therefore distinct, and that the result
of explicitly interning a computed string is the same string as any
pre-existing literal string with the same contents? Is there anyone who
needs to know about any of these arcane distinctions?
|
|
|
W 2/2/011
|
HW due:
1. If you do not already have a JVM installed on your machine, visit
www.java.com to download Java.
2. Visit www.eclipse.org and download the appropriate Eclipse IDE onto your computer.
If you do not know whether your operating system is 32-bit or 64-bit, do a
Google search on “determine 32-bit or 64-bit” and follow the instructions at
the support.microsoft.com website.
3. Unzip the entire set of Eclipse distribution files (approx. 130 MB,
uncompressed) to a location such as C:\eclipse. You may use whatever location
you wish, but in the remainder of these instructions, I will assume that you
have used C:\eclipse.
4. Execute the file C:\eclipse\eclipse.exe. Note: Do not execute eclipsec.exe.
5. When Eclipse appears (you may have to wait a long time), respond to the
question about where you want your default file location to be. I recommend
something like C:\!data\ipl, but you can use your own judgment on this.
6. When the main Eclipse menu appears, issue the menu commands File, New,
Java Project.
7. In the Project Name box, type Hello1. Accept all the defaults. Make sure
that under the heading of JRE (Java Runtime Environment), you have chosen
something. On my machine, it is JavaSE-1.6, but your personal situation may
vary.
8. Click the “Next” button.
9. Click the “Finish” button.
10. Issue the menu commands File, New, Class.
11. In the Name box, type Hello.
12. Important: After the question
“Which method stubs would you like to create?” be sure you mark the one that
says public static void main(String[] args). Leave the “Inherited abstract
methods” also marked, by default.
13. Click the “Finish” button.
14. You should now see a program that resembles the “Hello, world” program on
p. 7 of your textbook. Press Ctrl+A to select the entire program, and press
DEL to delete the text. The program should now be blank.
15. Type the program from p. 7 of your textbook, line by line. Yes, you could
save a minute or two by copying and pasting, but it is good for you to
practice typing the actual syntax of Java code.
16. Press Ctrl+F11 to execute your program. With any luck, the system console
will display “Hello, world.”
17. In your written homework, write down any problems you encountered or
things you learned while performing these steps. If everything went
perfectly, also write that down.
|
|
|
Th 2/3/011
|
HW due: Perform Exercise
1.3 on pp. 10-11 and record all of the results.
|
|
|
F 2/4/011
|
HW due: Read pp. 23-29 (up
to §3.8 at the bottom of p. 29); write Exercise 2.1abc. (Either copy and
paste your program code into a word processing document that you print, or
write the code in pencil, line by line.)
|
|
|
M 2/7/011
|
No class.
|
|
|
T 2/8/011
|
HW due: Click here. This assignment should take you about an
hour and a half, but you have several days to do it.
|
|
|
W 2/9/011
|
HW due: Read §§4.1 through
4.7, stopping at the top of p. 39; write thoughtful answers to the following questions.
1. Write a class with a main routine (public static void main) that attempts
to answer the question posed at the very end of §4.7 by printing the results
of the following additions:
4+8
4+8.0
4.0+8.0
4+8.1
4.0+8.1
Which of these 5 examples involve type conversion?
2. In #1, when you run your program, what appears to be true, in general,
regarding type conversion in mixed expressions involving both ints and
doubles?
3. Near the top of p. 37, the author states, “Always remember that when you invoke a method, you do not have to
declare the types of the arguments you provide. Java can figure out what type
they are.” However, if Java can figure out the type of the argument that is
passed, Java can surely figure out at runtime what the type of the parameter
in the called method is; after all, that type must be the same as the type of
the argument that was passed. Therefore, why is it necessary to declare the
type of the parameter in the method that is called? In other words, why must the language require us to write
public
static void ping (String blob) {
/* body of method goes here */
}
instead of
public
static void ping (blob) {
/* body of method goes here */
}
?
Remember, when ping is called at
runtime, the type of argument passed to ping will always be known, since the
argument will be either a constant of known type, a variable of a type that
has already been declared, or a mixed expression whose type is determined by
well-defined type conversion rules. It would seem, maybe, that there is no a priori need for Java to require the
ping method to contain an additional declaration of blob as a String.
Is this requirement—that is, the requirement to declare the type of each
parameter used in a method—merely a language annoyance? Is it a redundancy?
Or is there a darned good reason for it? You will probably not find the
answer on the Internet, but if you think hard about it, you can puzzle this
out on your own. Explain your reasoning.
|
|
|
Th 2/10/011
|
HW due: Read §§4.8 through
5.1 (p. 39 to bottom of p. 48); write the exercises below.
Exercises
1. Enter the following FlorbTester class and test it by entering various
values in the output line of main. What is the purpose of the florb method,
in plain English? Try to be as economical in your wording as you can be, but
be sure that you have fully described florb for the benefit of anyone who
might want to use it.
2. Midway through the program listing, there is a line that begins
if
(floobie==0)
Predict exactly what would happen if you changed this to
if
(floobie=0)
Write down your prediction. Make your prediction specific. (In other words, don’t say, “The program will crash.”
Instead, if you think the program will crash, explain how you think the
program will crash, either at compile time or at runtime, and state a
reason.)
3. Make the change indicated in step 2. Was your prediction correct? (Write
“Yes” or “No.”) Explain what you learned, or if you learned nothing, explain
what it is that you were supposed to learn.
|
|
|
F 2/11/011
|
HW due: Read §5.2 to the
end of Chapter 5 (pp. 49-58); write Exercise 5.1.
|
|
|
M 2/14/011
|
No class. If you need help
with tomorrow’s HW, please come in during your free period or after school.
|
|
|
T 2/15/011
|
HW due: Read §§6.1 through
6.3 (pp. 65-67); write Exercise 5.7abcde.
This programming exercise is fairly challenging and must be done with recursive calls for full credit.
Unless you are already a Java genius, it is unlikely that you will be able to
do all 5 parts (a, b, c, d, and e) without help. Be sure to use the given
methods first, rest, and length to help you.
Depending on how quickly you figure out what is going on, Exercise 5.7 should
take you somewhere between 1 hour and 2.5 hours. Don’t delay! Get started
over the weekend of Feb. 12-13. Do as much as you can on your own, but then
you should ask a classmate or Mr. Hansen for help. The computer lab, MH-102,
will be open during periods C, D, E, and F, as well as after school on
Monday. Be sure to bring a printout of your program listing with you.
|
|
|
W 2/16/011
|
HW due:
1. (Everyone needs to do this.) Read §§6.4 through 6.9 (pp. 68-72).
2. Students who did not fully solve yesterday’s assignment by using recursion are expected to visit
the Computer Lab after school Tuesday (or before school Wednesday) and make
up the assignment completely.
|
|
|
Th 2/17/011
|
HW due: Read §6-10 (pp.
72-74), through the end of Chapter 6.
Big Vocabulary Quiz (40 pts.) on
Chapters 1-6. All terms in the Glossary sections at the end of each
chapter, as well as all terms discussed in class (such as LIFO, FIFO,
pattern, antipattern, “off by 1 problem,” requirements creep, etc.) may be
quizzed. You will have approximately 20 questions in 25 minutes. Some may be
fill-ins (given a definition, write the term being defined), and others may
be the other way around (given a term, provide the definition).
|
|
|
F 2/18/011
|
No school.
|
|
|
M 2/21/011
|
No school.
|
|
|
T 2/22/011
|
HW due:
1. Follow the advice given in the last line of §6.4. In other words, become
thoroughly acquainted with some powers of 2: 1, 2, 4, 8, 16, 32, 64, 128,
256, 512, 1024, 2048, 4096, 8192, 16384, 32768, 65536. Of special importance
are 20 = 1, 24 = 16, 28 = 256, 210
= 1024, and 216 = 65536, and you should know those by heart. As
for the rest, you should be able to recognize them, but you are not expected
to know the exponent instantly.
For example, you should instantly be able to recognize 8192 as a power of 2,
but it is not necessary to know instantly that 213 = 8192.
However, if you see 1024, you should instantly recognize it as a power of 2,
and at the same moment, you should know that 210 = 1024. Make a
table or a set of flash cards, practice the answers, and be prepared for a
possible oral quiz.
2. If someone asks you, “What is 2 to the 20th power?” (or 30th, or 40th, or
any other multiple of 10), be prepared to answer quickly with an estimate.
For example, 220 = (210)2 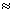 (1000)2 =
1 million. The exact answer is a little larger, namely (1024)2 =
1,048,576, but we do not care. The
important thing is that 220 is about a million. Thus 220
bytes equals 1 MB. Similarly, 230 bytes = 1 GB (about a billion
bytes), 240 = 1 TB (about a trillion bytes), 250 = 1 PB
(about a quadrillion bytes), and 260 = 1 EB (about a quintillion
bytes). When learning these, I recommend using TB (terabyte) as an anchor,
since the letter “T” in terabyte reminds us of trillion, which is a million million, or therefore about 220
times 220, or 240.
3. How many different keys can be generated using 1024-bit encryption? The
answer is 21024, which is approximately 21020, which is
(210)102, which is about (103)102,
or 10306. Final estimate: 10306, which is indeed a large
number: 1 followed by 306 zeros. Question: Is this estimate lower than the
true value, or higher than the true value, and by approximately what factor?
Warning: You will not be able to
use your TI-83 or TI-84 calculator to answer this question, because your
calculator overflows at 10100. Thus you will have to think.
Remember to include both sources of error: (1) the fact that 21024
does not really equal 21020, and (2) the fact that 210
does not really equal 103.
4. On p. 76, do either Exercise 6.4 or Exercise 6.5 (your choice). The word
“iterative” means “involving iteration.” In other words, use a loop, not
recursion, to accomplish the task. These methods will involve a few more
steps than their recursive counterparts, but there is no danger of stack
overflow with iteration.
Warning: If your computer appears
to lock up, but if the disk access light is not on, then you may have created
an infinite loop. Make sure that your loop body includes a statement to
increment or decrement your loop counter.
5. Explain why the following method is not
acceptable for Exercise 6.4, even though it works correctly:
public static double power(double x,int y) {
return Math.pow(x,
y);
}
|
|
|
W 2/23/011
|
No additional HW is due today. However, please use
algebra to prove that the answer to #3 in yesterday’s assignment is “lower”
by a factor of 180, to the nearest whole number.
|
|
|
Th 2/24/011
|
HW due: Read Chapter 7 (pp. 79-86); write Exercise
6.6a. Your myexp method will
simulate the behavior of exp(x),
the natural exponential function. On your TI-83 or TI-84 calculator, this
function is the “2nd” function of the LN key, which is rendered on the
calculator’s screen as e^( . Note that myexp must accept two arguments, namely a double to specify what x
value to use, and an int to
specify the highest exponent to use.
For example, if x = 1.09, and if x = 4, then we can use the calculator
to find exp(1.09) 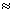2.974. Try it and
make sure that your calculator agrees with mine! Your myexp method should add up the following values:
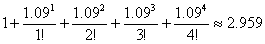
Note that 2.959 is not exactly correct, since the true answer is about 2.974,
but we would get a better answer if we used n > 4. Similarly, if x
= 1.955 and n = 9, then your myexp method should add up the following values:
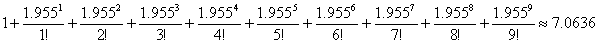
This result compares quite favorably with the answer your calculator gives
for exp(1.955), namely 7.0639.
Hint: Your myexp method will always start with a partial sum, which
you might call double partialSum,
with an initial value of 1. Then, you use a loop that cycles through a total
of n times to add the following to
partialSum: x to some power,
divided by that power factorial. When the loop finishes, partialSum will
contain a value that you can return.
If you do not finish this exercise by Thursday, we can take some extra time.
However, I expect everyone to have at least a good start on this before class
starts on Thursday: method body, declaration of double
partialSum, and a loop that looks
as if it is modifying partialSum in a plausible way. If necessary, we will
work together to get our methods to work properly, but we need to have
something to start from.
|
|
|
F 2/25/011
|
HW due: Read §§8.1-8.5 (pp. 91-93) and at least 1
more page of the
HBGary story; write a modified version of main for yesterday’s myexp method in order to print the estimates for exp(1.2)
using maximum exponents of 2, 4, 6, and 8. Separate your output with a tab
character ("\t") between each output value.
Your output should look like this:
2.92 3.2943999999999996 3.319283199999999 3.320100790857142
Note: In class, we came close to
having a working version of myexp, except that we forgot to increment our loop
variable, and our end condition was wrong.
|
|
|
M 2/28/011
|
No class.
|
|