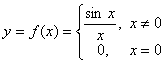|
AP Calculus AB / Mr. Hansen |
Name:
_________________________ |
Sample Test
Time limit: 32 minutes (48
minutes for extended time).
Calculator is permitted for all problems.
Do not spend too much time on any single problem.
Clues to some problems that you cannot solve initially may be found elsewhere
in the test.
All problems are free-response.
Use appropriate mathematical notation. Legibility counts.
|
1. |
Sketch a function f that is not defined at x = 3 and has a step discontinuity
there. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
Explain clearly why, even
if #1 is modified so that the function is
defined at x = 3, the function
cannot possibly be differentiable there. Try to consider at least two
different cases, i.e., different ways in which the function can be defined at
x = 3. A formal proof is not
expected. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
State the IVT. Standard
abbreviations are encouraged. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
Let |
|
|
|
|
|
Explain clearly in what
way(s) the given function violates the hypotheses of the IVT for any closed
interval that includes 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
5. |
Prove, rigorously, that even
though function f in #4 violates
the hypotheses of the IVT for [−2.356, 0.786],
a closed interval that includes 0, the IVT conclusion is nevertheless true. You
may find a sketch to be helpful, but a sketch is not required. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. |
Sketch a function that
violates both the hypothesis and the conclusion of the IVT. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7. |
Sketch two functions f and g that are continuous on  and have the property that f (a) > g(a),
while f (b) < g(b), where a < b. Let h(x)
= f (x) − g(x), and take it as a given that the
difference of continuous functions is continuous. Prove that |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8. |
Let h(x) = x3 – 10x2 + 3x +
31. |
|
(a) |
Suppose that someone doubts
that this polynomial function is continuous. (We already know that all
polynomials are continuous, but assume that there is someone who did not get
the memo.) Use the definition of continuity (all 3 parts) to prove
that h is continuous on [2, 3].
Limits can be proved using limit properties; no need for epsilons and deltas
here. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(b) |
Compute the sign (+ or
–) of h(2) and of h(3). (Exact values of h(2) and h(3) are not required.) |
|
|
|
|
|
|
|
|
|
|
(c) |
What does IVT allow you to
conclude from (a) and (b) regarding roots? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9.(a) |
Sketch a continuous function
f that has a cusp at x = 1.5, such that f is differentiable on |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(b, c) |
What role does the line x = 1.5 play for f ¢ ? for f itself? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10. |
Find |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11. |
Solve the following
differential equation for y subject
to the initial condition (2, −1): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12. |
In #11, compute y when x = 2.3. (Note that this question can be answered even if you
were unable to answer #11 itself.) |