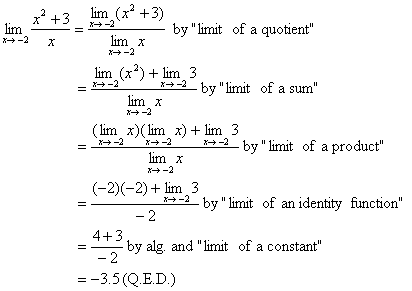|
9.
|
0.1644 . . . . , which we
must round down to 0.164
To see this, put the function itself into Y1, the constant value
1/3−0.0015 into Y2, and the constant value 1/3+0.0015 into Y3.
Use 2nd CALC 5 (intersection finder) to find the places where the function
breaks out of the 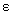 band, which is
denoted by the lines for Y2 and Y3. Save those x values as A and B in your
calculator’s memory (keystrokes: 2nd QUIT X STO A ENTER, then use 2nd CALC to
find the other intersection and use 2nd QUIT X STO B ENTER). In this problem,
the role of c is played by the number band, which is
denoted by the lines for Y2 and Y3. Save those x values as A and B in your
calculator’s memory (keystrokes: 2nd QUIT X STO A ENTER, then use 2nd CALC to
find the other intersection and use 2nd QUIT X STO B ENTER). In this problem,
the role of c is played by the number 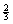 , and you can easily compute |c − A| and |c −
B|, both of which are approximately 0.1644278733. , and you can easily compute |c − A| and |c −
B|, both of which are approximately 0.1644278733.
In this problem, it so happens that the distance from c to the point (A) where the function violates the 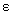 band on the left
equals the distance from c to the
point (B) where the function violates the band on the left
equals the distance from c to the
point (B) where the function violates the 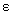 band on the right.
In some problems, you need to look at both distances and choose the minimum of the two in order to ensure
that your punctured band on the right.
In some problems, you need to look at both distances and choose the minimum of the two in order to ensure
that your punctured 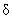 -neighborhood will be small enough. Always be sure to round
down in problems of this type. This one is easier than the average problem of
this type, however, since |c −
A| and |c − B| are the same,
and nobody would be tempted to round up. However, be aware that even if the
computed distance had turned out to be, for example, 0.164999, you would
still need to round down to 0.164 in order to obtain “the largest 3-place
value of -neighborhood will be small enough. Always be sure to round
down in problems of this type. This one is easier than the average problem of
this type, however, since |c −
A| and |c − B| are the same,
and nobody would be tempted to round up. However, be aware that even if the
computed distance had turned out to be, for example, 0.164999, you would
still need to round down to 0.164 in order to obtain “the largest 3-place
value of 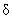 ” as instructed. ” as instructed.
|
|
13.
|
1.043
In 2010, you will be shown exactly how to present work in problems of this
type before you are expected to show work for credit on a test. However,
finding a trapezoidal estimate without showing the work is a legitimate
possible question for the 9/28/2010 test. Here is how you would do it with
your calculator:
First, put the function X^2−3 into Y1. Then, use STAT EDIT
to store your x values into list L1.
Clear list L1, if necessary, by placing your cursor directly over
the L1 and pressing ENTER CLEAR ENTER. Then enter the x values (namely, 1.23, 1.565, 1.9,
2.235, and 2.57) into list L1, pressing ENTER after each one.
Then, clear list L2 if necessary, and redefine L2 as
ENTER Y1(L1) ENTER. Note that
you must enter this definition by pressing the first ENTER while your cursor
is directly over the L2, not
when the cursor is in the first entry of list L2.
The basic idea of the trapezoidal rule is to take an estimated “average”
function value over each subinterval, times the width of the subinterval,
which is 0.335 in this case. (That is exactly what you did in geometry when
you learned the area formula for a trapezoid.) Add up the products, one for
each of the 4 subintervals, and you should get approximately 1.043.
Since we do not know the true average value of the function over each
subinterval (this is a nonlinear function, after all), we do the next best
thing: We take the mean of the value at the left endpoint and the value at
the right endpoint. For example, on the final subinterval, from x = 2.235 to x = 2.57, the function value is 1.995225 at the left
endpoint and 3.6049 at the right endpoint. Averaging these gives 2.8000625 as
a reasonable estimate of the average value of the function on that
subinterval, and multiplying by the interval width, namely 0.335, gives
0.9380209375 as the estimated contribution to the definite integral. Adding
that to the other subinterval contributions (note: some of which may be negative) gives a final answer of
1.043, which is reasonably close to the true value of about 1.0179.
More subintervals would give better accuracy, of course, but on the AP exam
you will almost never be required to use more than about 4 or 5 subintervals.
|
|
15.
|
(a) miles
(b) net distance traveled, in miles
[Note: Over intervals of time where
the velocity is negative, the distance traveled will be decreasing, and over
intervals of time where the velocity is positive, the distance traveled will
be increasing.]
(c) speedometer (though, on most cars, only when
traveling forward)
(d) derivatives
(e) The definite integral’s units are the same as the area units. The
horizontal axis measures distance (mi.), and the vertical axis measures mpg.
The area units are thus miles squared divided by gallons, which are
meaningless for what we are trying to accomplish.
(f) Instead of recording mpg, record the reciprocal of the displayed numbers
(i.e., gallons per mile). The product of gal./mi.
and miles will be gallons as desired.
|