|
T 3/1/011
|
HW due: Read the material below; write the proof
that follows the reading material and §10-7 #1, 2. Then, log your points!
Supplementary reading material:
The notational conventional we will use, as discussed in class last Friday,
is angle brackets for the coordinates of a vector, .e.g., <1, 2> for
the vector that goes 1 unit in the x
direction and 2 units in the y
direction. We indicate vectors through the use of an arrow over the letter, since
boldface (the notation typically used on the AP exam) is inconvenient.
Finally, we will use double vertical bars to indicate the norm (“magnitude”)
of a vector, not the single vertical bars used in your textbook. For example,
if vector 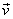 has components
<1, 2>, we will write has components
<1, 2>, we will write 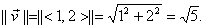
The dot product of two vectors is
defined in #14 on p. 546. Please take a moment to glance at that page now.
The dot product of two vectors is defined to be either
(a) a real number equal to the
product of the vector norms and the cosine of the angle between them, or
(b) more conveniently, a real number
equal to the product of the first components added to the product of the
second components. For example, if vector 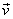 has components
<1, 2>, and if vector has components
<1, 2>, and if vector 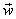 has components <−3,
6>, then has components <−3,
6>, then 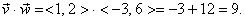
A common AP-type problem is to compute the tangential and normal components
of the acceleration vector, 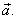 For example, if the
position vector is <et,
sin t>, then For example, if the
position vector is <et,
sin t>, then 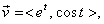 and and 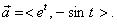 If our task is to
compute the tangential and normal components of acceleration when t = 1.5, then we begin by finding If our task is to
compute the tangential and normal components of acceleration when t = 1.5, then we begin by finding 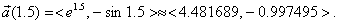 The velocity vector
is The velocity vector
is 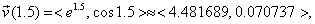 and the projection
of and the projection
of  upon upon  has length has length 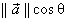 by simple
trigonometry. This length is a scalar
(i.e., a real number), and if we multiply that length by a unit vector in the
direction of by simple
trigonometry. This length is a scalar
(i.e., a real number), and if we multiply that length by a unit vector in the
direction of 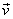 , namely , namely 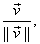
we should obtain the tangential component of acceleration, namely 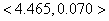 to 3 decimal places. to 3 decimal places.
When we say “tangential component of acceleration,” we mean that we are
intending to decompose the acceleration vector into two perpendicular
components: one called 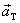 that is tangential
to the current motion, i.e., following with or against the velocity vector,
and one called that is tangential
to the current motion, i.e., following with or against the velocity vector,
and one called 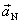 that is normal to
the current motion. The that is normal to
the current motion. The 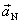 vector is easy to
compute: It is simply whatever satisfies the equation vector is easy to
compute: It is simply whatever satisfies the equation 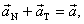 and we can figure
that out simply by writing out the components and solving. and we can figure
that out simply by writing out the components and solving.
As for the 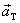 vector, it can be
solved, as described above, by multiplying the scalar vector, it can be
solved, as described above, by multiplying the scalar 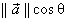 by the vector by the vector 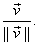
Problem: Accept the result of #14
on p. 546 as a given; i.e., that the dot product definition (b) above is
valid. Prove that 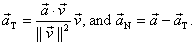
[Note: Feel free to use these
formulas when solving #1d and #2d.]
|
|
|
W 3/2/011
|
HW due: Read §§11-1 and 11-2; rewrite (even if they were
correct the first time) §10-6 #10, 12; write §10-7 #4, 12, 14. Then log your
points.
|
|
|
Th 3/3/011
|
HW due: Read §11-3 and the material below; write the
problem below, §11-2 #4, 6, and §11-3 #12. Then log your points. Note: We will be skipping §§11-4 and
11-5.
Supplemental reading:
Recall that the volume formula for cylindrical shells is 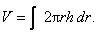 Did you happen to
notice that the integrand is simply the lateral area formula for a cylinder?
One way to think about this (slightly different from the cake slicing
approach) is to think of a cylinder with lateral area Did you happen to
notice that the integrand is simply the lateral area formula for a cylinder?
One way to think about this (slightly different from the cake slicing
approach) is to think of a cylinder with lateral area 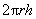 , where the lateral area is multiplied by dr in order to create dV, a little bit of volume. In a
similar way, we could use spherical shells to build up the volume of a
sphere. The analogous formula, since the surface area of a sphere is , where the lateral area is multiplied by dr in order to create dV, a little bit of volume. In a
similar way, we could use spherical shells to build up the volume of a
sphere. The analogous formula, since the surface area of a sphere is 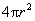 , would be , would be 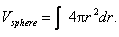
Problem:
Use the concept of spherical shells in order to prove the standard volume
formula for a sphere.
|
|
|
F 3/4/011
|
HW due: Read §11-6; write §11-3 #14, §11-6 #8, 11,
12, 13. Then log your points.
|
|
|
M 3/7/011
|
No additional HW due. This is your chance to get
some sleep and/or catch up on older assignments.
However, you do have a test coming up tomorrow, and you will need to do some
studying over the weekend anyway. Suggested optional review problems:
pp. 549-550 #R2, R3, R4, R5a, R6b, R7b
pp. 592-593 #R2, R3, R6
p. 596 #T3
Answers (without worked solutions) are posted at hwstore.org
so that you can see how well you did.
In class: Review, including any of the suggested review problems that you may
wish to see worked in detail.
|
|
|
T 3/8/011
|
Test (100 pts.)
on Chapters 10 and 11.
|
|
|
W 3/9/011
|
HW due: Read §12-1; write §12-1 #1-7 all plus #5 from yesterday’s test. If you wish, you may
revisit any of the other problems from yesterday’s test as well, especially
#1, which is actually a related rates problem if you think about it.
Then, remember to log your points!
|
|
|
Th 3/10/011
|
HW due: Read §12-2 and #8d on p. 606; write §12-2
#4, 8abc. Then, log your points and take Mr. Hansen’s AP poll.
|
|
|
F 3/11/011
|
HW due: Read §12-3; write §12-3 #1-11 all. Then log
your points.
This is one of those “learn by doing” sections. I can do it for you and have
you watch, or you can do it for yourself and learn as you go. (Hint: The second approach works much
better if the objective is learning.)
Regarding the AP poll, we have 100% of students signed up for both the
practice exam and the real AP exam. The latter is “required” in the sense
that everyone is expected to take it, but of course there is no way to force you to take it.
|
|
|
M 3/14/011
|
Pi Day!
HW due: Read §§12-4 and 12-5; mark up your book as indicated below; start
memorizing the green boxes on p. 616 and the associated intervals of
convergence; write §12-4 #6abc, 7. Then, remember to log your points.
Mark-ups to your book:
1. On p. 615, heavily underline or circle the word could in the
statement of #6c. It is important for you to understand that simply because
the terms approach zero, that is no guarantee that the series must converge.
The classic counterexample is the harmonic series, 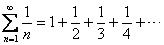 , ,
which diverges by comparison with the divergent improper integral 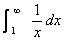 . (For the proof, see your class notes from Friday, 3/11.) . (For the proof, see your class notes from Friday, 3/11.)
2. On p. 616, the preamble should say “expansion about x = a” (typo).
3. Another typo: Near the middle of p. 623, change the equation 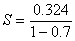 to to 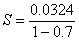 . .
4. On p. 636, near the middle of the page, change the 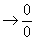 notation to notation to 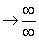 . .
5. On p. 651, in #R6b, insert the word “of” between “interval” and
“convergence.”
6. On p. 651, in #R6c, change the phrase “Write the fifth five terms” to
“Write the first five terms.”
7. Finally, if you have not already done so, mark all the intervals of
convergence for the “Eight Well-Known Power Series” on p. 616: 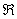 for the first five,
then (0, 2] for the ln x series, (−1,
1) for the geometric series, and [−1, 1] for the arctan x series. Sometime before spring
break, we will have a memory quiz on the eight series and their intervals of
convergence. for the first five,
then (0, 2] for the ln x series, (−1,
1) for the geometric series, and [−1, 1] for the arctan x series. Sometime before spring
break, we will have a memory quiz on the eight series and their intervals of
convergence.
|
|
|
T 3/15/011
|
No additional written HW due. In class, we will have
a “Regurgitation Quiz” in which
you will be required to state any 3 of the famous series on p. 616 (your
choice), together with their intervals of convergence.
|
|
|
W 3/16/011
|
Today we will have the second “Regurgitation Quiz” with any 6 of the famous series on p. 616
(your choice), together with their intervals of convergence.
HW due: Read §12-6 and the green boxes on p. 630; write §12-5 #9, 13 (2
different ways), 15, §12-6 #8, 13, 24, 25. Then log your points.
|
|
|
Th 3/17/011
|
HW due: Prepare for the final “Regurgitation Quiz” covering all 8 of the famous series on p.
616 and their intervals of convergence; read §12-7, especially the green
boxes on pp. 634-635; write §12-6 #14*, 19. Then, log your points.
* Please make the following typo correction in #14: There should be an xn in the numerator of the
expression for the general term.
Note that the proof of the green box on p. 632, which is sketched in §12-7
#23, relies on a “sleazy trick”: invoking a postulate to cover the situation.
Since the given postulate is equivalent to the completeness of the reals,
which is really beyond the scope of our course, §12-7 #23 will not be
assigned as homework. However, you can do it if you wish, since it is a
convenient review of the rigorous definition of a limit.
|
|
|
F 3/18/011
|
No additional HW due. However, please compute the
derivative of xx so that
we can resume with that loose end from yesterday’s discussion.
Since the quarter ends today, all HW logging needs to be complete by 3:00 p.m. Also, any extra-credit
crossword puzzles from www.mathcross.net
that are in hard-copy form must be submitted by 3:00 p.m. in room MH-102. Crossword puzzles in e-mail form will
be accepted until noon on Thursday, March 24. Any received after that cutoff
time will be credited to your fourth quarter average.
|
|
|
|
Spring break.
|
|