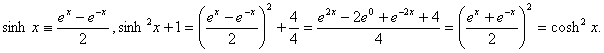Monthly Schedule

(Honors AP Calculus, Period A)

T 2/1/011

HW due: Correct yesterday’s test until it is 100% correct, glowing with legible, clear, sparkling presentation of all the problems. Copying from other students is not permitted, but you may use any helpful resource you wish to spur your creative juices as long as you document such resources.

Example: “I had no idea how to do the radial slicing until I reviewed my notes and double-checked with Bogdan. Then I used the radius to the centroid, integrated the area function times  from 0 to , and voila!”

 

W 2/2/011

HW due: Write §9-2 #1, 3, 5, 11, and the problem below.

Problem: Let R be the region in Quadrant I to the right of the line x = 1 and bounded by the parabola y = 9 − x2. Use both plane slicing and the method of cylindrical shells to prove that the volume of the solid of revolution formed by revolving R about the line y = −3 is exactly  cubic units.

Hint for #11 (read this only if you are stuck): Let u = ln x, dv = dx.

 

Th 2/3/011

HW due: Read §9-4; write §9-3 #3-31 eoo plus 30. That is a total of 9 problems, all required.

Chocolate challenge (optional): The student with the best writeup of #26 will win a chocolate bar.

 

F 2/4/011

Optional Retest, 7:00 a.m., MH-102. The format will be exactly the same as the first test: an optimization problem, a plane area, a volume by 2 or more methods, a polar problem (area or arc length), and another arc length problem. Your score on the previous test will be e-mailed to you by approximately 10:00 p.m. Thursday so that you can make a decision on whether or not to attend. Remember, a single low test score, by itself, rarely has much impact on your quarter grade.

HW due: Read §9-5; write §9-4 #9, 13ab, 18ab. Note: There are 6 typos in problems 7-12. All the “n = 0” lines should instead say “.”

Additional note: The original assignment was for #13b and #18b instead of parts (a) and (b). Of course, this was also a typo! In class on 2/4, we did #13a and #18a, and you were asked to add the solutions to your homework paper.

 

M 2/7/011

HW due:

1. Please read the entire key from the Jan. 31 test. The solutions are in red, and the scoring rubric is in pencil in the left margin. Make sure that all your points were recorded correctly.

2. Skim §9-6. This is not an AP topic, and although we will cover it in class, we will not go into much depth. Reading notes are optional for this section.

3. Read §9-7 and the partial fraction decomposition tutorial with practice problems. Doing some of the practice problems is strongly recommended. That is how everyone will learn in the school of the future! Reading notes are required here, as usual.

4. Write §9-7 #1, 3. If for some reason (cough, cough) you are unable to attend class today after Super Bowl XLV, you may turn in the assignment tomorrow for full credit.

 

T 2/8/011

HW due: Read §9-8; write §9-7 #2-12 even, 19, 23ac.

 

W 2/9/011

HW due: Read §9-9; write §9-8 #1-6 all, 10.

 

Th 2/10/011

HW due: Read §9-10 and the loose end below; write §9-9 #27, 34, and the Nifty Cosh Property Problem below.

Nifty Cosh Property Problem

Let f (x) = cosh x. Prove that for any interval [a, b], the arc length of function f from a to b is numerically equal to the area under the graph of f from a to b.

Loose End

On Monday, we proved that

which looks similar to the result obtained from WolframAlpha.com or a table of integrals, namely

 However, those second terms look suspicious. Why do they not match?

We need to show that  has the same derivative as . The first one has derivative






and the second one has a derivative that can be found by implicit differentiation. If  then  which we can differentiate implicitly to get

At this point, it suffices to show that  i.e., that

Typing cosh(arsinh t) into WolframAlpha.com returns  but that is not very satisfying. Here is a better proof.


Claim:

Proof: Since  We can employ that well-known identity, namely sinh2 x +1 = cosh2 x, to get  which leads to

    

 

F 2/11/011

HW due: Write §9-10 #2-8 even, 9-19 odd, 22c (no work), 23, 25abcdj.

 

M 2/14/011

HW due: Review problems on pp. 498-500 #R3, R4, R5f, R6c, R7a, R8, R9c, R10, R11h. Try to finish all of these over the weekend, but if you cannot, you still have another night to work on them before the test.

In class: Review.

 

T 2/15/011

Test (100 pts.) on Chapter 9. There will also be a question or two from Chapter 8.

An example of a “Chapter 8” question would be to find the area and perimeter of the figure described in #R5f on p. 498. Or, you could be asked to find a volume (good practice problem: #10 on p. 471, using both washers and shells). Other than that, the practice test on pp. 501-502, omitting #T11a, is representative of the length and difficulty you should expect.

If you need additional practice problems, try these links related to the Chapter 8 retest:

 

W 2/16/011

HW due: Completely rewrite yesterday’s test (note correction to #2), as well as the banana slicing problem below. As for #2 on the test, it appears that the only fair way to grade it will be to give everyone the full points allocated for that problem.

Banana Slicing Problem:

Let R be the region in Quadrant II between the circle x2 + y2 = 11 and the ellipse

(a) Sketch R, showing all salient points (intercepts, points of intersection).

(b) Compute the area of R.

(c) Compute the perimeter of R.

(d) Mud will be piled onto R (in the third dimension) so as to create a solid having base R in the xy-plane. All cross sections perpendicular to the y-axis are to be semicircles. Does the solid formed in this way most closely resemble a banana, a half banana, or a quarter banana? (Choose one.)

(e) Compute the volume of the solid described in part (d).

 

Th 2/17/011

HW due: Read §§10-2 and 10-3; write §10-2 #1-5 all. Note that the instructions for #1-4 are on the previous page.

 

F 2/18/011

No school.

 

M 2/21/011

No school.

 

T 2/22/011

HW due: A minimal assignment to celebrate the long weekend! All you have to do is click here and enter a score of 4 for the 2/22 assignment. This will become our new procedure for logging HW points.

Update: All 14 students have successfully executed this assignment. Congratulations!

 

W 2/23/011

HW due: Read §10-4 and this on-line tutorial; write §10-3 #11, 12, 15, §10-4 #1, 2. When finished, use the link at the top of the schedule to enter your score.

 

Th 2/24/011

HW due: Read §10-5; write §10-4 #5, 11, 13, 18. When finished, remember to log your points.

 

F 2/25/011

HW due: Read §10-6 (reading notes optional); write §10-5 #3, 10, 11, 12, 13 (optional), 14ab. Then, log your points!

 

M 2/28/011

HW due: Read §10-7; write §10-6 #10, 12. Then, log your points.

 

 

Return to the HappyCal Zone

Return to Mr. Hansen’s home page

Return to Mathematics Department home page

Return to St. Albans home page

Last updated: 01 Mar 2011, link errors corrected 09 Feb 2013