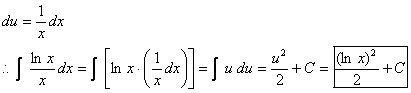|
M 11/1/010
|
No additional HW due. Class
today (or tomorrow, if it rains today) will be outdoors. Your classroom is
the entire Cathedral Close. If you are new to the school, or if you have not
explored the Close much, you will want to read pp. 39-42 (Appendices A and B)
of the STA
School Handbook in preparation for today’s event, which is the
FIRST-EVER HAPPYCAL
PUZZLEMANIA SCAVENGER HUNT EXTRAVAGANZA.
When you arrive at the start of class, you will be given a map of the Close
and a cryptic clue to get you started. The grand prize is a pound of
chocolate and 3 bottles of boredom repellent spray, enough for each member of
your group. (Note: The most
requested prize was a 10-point bonus, but everyone already gets 10 bonus
points on the first day of the new quarter anyway.)
After you have solved all the calculus-based puzzles hidden at the various
puzzle locations throughout the Close, you must return to the classroom to
receive your final clue, which will (maybe) allow you to assemble the answers
to the puzzles in such a way as to lead you to the prize. Good luck!
Team 1: Taylor, Nicky, Martin
Team 2: Sandy, Jonathan
Team 3: Austin, Miles, Alex
Team 4: Bobby, Michael, Steven
Team 5: Will, Bogdan, Nathan
Ground rules: If another group overhears your strategizing and steals your
ideas, that is not considered cheating. Therefore, you may wish to hold your
brainstorming meetings out of earshot. (Or, if you are clever, you might try
to spread disinformation among the other groups.) However, the following are
not permitted and will be considered cheating:
1. It is cheating (and a violation of school rules) to use cell phones, text
messaging, or walkie-talkies. Play fair, gentlemen!
2. It is cheating and dishonorable to disrupt, move, steal, hide, or
otherwise tamper with any box containing puzzle cards. You need to leave the
boxes undisturbed for the next team to find.
3. It is cheating, not to mention rude and disruptive, to shout or run
indoors. Behave properly indoors. Outdoors is where you can let off some
steam.
4. It is cheating to physically detain or harass other team members. You must
give everyone a fair chance at the prize.
Permitted strategies you might want to consider:
1. It might be wise to have a trailing lookout to guard against having other
teams follow you.
2. You may use the computer lab (MH-102) as a location for sending and
receiving e-mail.
3. I recommend staying together as much as possible. Three brains are much better than one. Since everyone
will eventually find all the puzzle problems, don’t think you are winning
just because you found all the puzzle locations first. The final puzzle,
where you have to assemble the parts to find the prize, is a doozy.
4. Trading information with other groups (“We’ll tell you where ____ is if
you tell us where ____ is”) is permitted.
|
|
|
T 11/2/010
|
No additional HW due today.
Mr. Hansen needs a day to recover (after waking up at 3:30 yesterday morning
for the puzzlemania). However, older assignments, especially assignments that
have been covered in class, may be rescanned.
If anyone other than the teams that have already won prizes would like to
submit worked-out solutions to the
four puzzle problems, small consolation prizes will be available.
|
|
|
W 11/3/010
|
HW due: Read §5-3; prepare
§5-3 #7-38 all for oral presentation; write #39-40.
Regarding grade reports, please send me an e-mail with double underscore at
the beginning of the subject line and your name, as follows:
__Flanders, Fred
In the body of your message, include your birthdate and one of your test
scores in order to verify your identity. (After all, on the Internet, anyone
could claim to be you, and by the time I figured out the problem, it would be
too late—your personal grade data would have been intercepted by someone
else.) Alas, your fearless teacher left the pile of e-mail addresses at
school by mistake.
|
|
|
Th 11/4/010
|
HW due: Read §5-4; write
§5-4 #3-42 mo3, 44. Feel free to use Troy’s
Integral Approximation Thingy to perform the trapezoid rule computation.
|
|
|
F 11/5/010
|
No school (teacher work
day).
|
|
|
M 11/8/010
|
HW due: Read §§5-5 and 5-6;
correct the inconsistent spelling of Riemann (pronounced REEE-monn) in the
middle of p. 196 so that both occurrences are “Riemann”; write §5-5 #1, 4, 7,
8, 11. Please use the Thingy (see link in 11/4 calendar entry) to
double-check your work and to accomplish the computations in #11.
|
|
|
T 11/9/010
|
HW due: Read §5-7; write
§5-6 #1, 11, 30, 32.
|
|
|
W 11/10/010
|
HW due: Read §5-8 and this handout; write §5-7 #1-6 all.
Later this week (but not today), you will be responsible for the proofs that
FTC1 implies FTC2 and FTC2 implies FTC1 (i.e., the converse).
|
|
|
Th 11/11/010
|
HW due: Read §5-9 and Braxton’s direct proof of FTC2;
write §5-9 #1-29 odd.
|
|
|
F 11/12/010
|
HW due: Read §5-10; write
§5-10 #3, 4, 5, and provide a written reason for each step in the handout proving the equivalence of
FTC1 and FTC2. (You may write directly on the handout if you wish.)
|
|
|
M 11/15/010
|
HW due: Review problems on pp.
241-243 #R1, 2, 3, 5, 6, 8, 10. You will probably not finish all of these for
today. Do as many as you can, and do the rest in preparation for tomorrow’s
test. The review problem set will be collected and scanned on Tuesday.
|
|
|
T 11/16/010
|
Test (100 pts.) through §5-10. During the test, your review problems (#R1, 2, 3,
5, 6, 8, 10) will be scanned. Be sure to bring them with you!
The test will begin at 7:50 a.m. in MH-312, but the difficulty will be such
that a well-prepared student who arrives at 8:00 should still be able to
finish by 8:50.
Study checklist:
1. The only famous mathematician whose name occurs on this test is Riemann.
However, essentially everything else we have discussed this year is
potentially something that could be included on the test. For example, the
product rule, the quotient rule, and the chain rule are not listed below,
since by now it is assumed that you are familiar with them.
2. Definition of continuity.
3. Definition of derivative.
4. Definition of indefinite integral (a.k.a. antiderivative).
5. Definition of the definite Riemann integral.
6. Derivative formulas for trig and inverse trig functions.
7. Memory aid 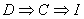 , which means, among other things, that Riemann
integrability is a weaker condition than continuity. , which means, among other things, that Riemann
integrability is a weaker condition than continuity.
8. Ability to reproduce all or part of the proof (with reasons for each step)
that differentiability implies continuity (p. 154), as well as the proof
(with reasons for each step) that FTC1
and FTC2 are equivalent.
9. Familiarity with (i.e., ability to provide any missing reason for) the
book’s proof of FTC1 (pp. 216-217) and Braxton’s direct proof of FTC2.
Thorough memorization is not expected and will not be tested for these two
proofs.
10. Finally, you must be able to state the complete hypotheses and
conclusions for EVT, IVT, MVT, FTC1, and FTC2.
|
|
|
W 11/17/010
|
HW due: Read §5-11; write
§5-11 #1, 3, and the problem below.
Problem: Suppose that we have a
function that is continuous on a closed interval, and suppose that we
subdivide that closed interval into an even number of intervals (i.e., using
an odd number of mesh points). Number the mesh points 0, 1, 2, . . . , 2n − 1, 2n. Let M designate the
Riemann sum formed by using odd-numbered mesh points, i.e., the midpoint sum
formed from double-width intervals. Let T
designate the trapezoid rule approximation formed by using only the
even-numbered mesh points. Finally, let S designate the Simpson’s Rule
approximation as defined on p. 233. Prove
that 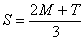 , which is a weighted average of M and T. , which is a weighted average of M and T.
|
|
|
Th 11/18/010
|
HW due: Provide some anonymous feedback on your HappyCal experience; read
§§6-2 and 6-3; write §6-2 #1; §6-3 #3-45 mo3 plus #43. For the later
problems, use the technique of “u
substitution” as shown by the example below. I realize that some people can
do the “u substitution” in their
heads, but I would like you to show the steps explicitly, at least for now.
46. Let u = ln x.
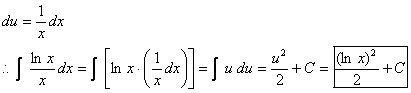
|
|
|
F 11/19/010
|
HW due: Read §§6-4 and 6-5;
write §6-3 #44 (using FTC1), prove the two theorems below, and then write
§6-3 #47-54 all. Also, if you did not explicitly show your formal “u substitutions” in yesterday’s
assignment, go back and add those. We know that the process has value, since
two of the student answers on the board were wrong, and the reason is most
likely that the authors were trying to do too much in their heads all at
once.
As has been the case ever since you took geometry two or three years ago, a
proof must include the “given” and “prove” statements as part of the writeup.
Otherwise, your paper will not clearly identify the hypotheses and conclusion
that constitute the theorem. Be sure to write “Q.E.D.” or the Halmos sign ( 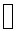 ) at the end. ) at the end.
Given: 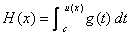 , where u is a
differentiable function, g is a
continuous function, and , where u is a
differentiable function, g is a
continuous function, and
c is a constant. [Note that H(x)
is a generalization of the accumulator functions we saw previously.]
Prove: 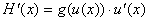
The result above is sometimes called the Chain Rule for Integrals, or CRI for
short. Hint: Use FTC1 to prove CRI.
Given: Constant
k is equal to qr, where q is
a positive real number and r is any real number.
Prove: We can
rewrite k as exp(r ln q). [The notation “exp” means “exponential function with base e.”]
|
|
|
M 11/22/010
|
HW due: Read §6-6; write
§6-4 #12, 13*, §6-5 #19-24 all, 37, 39.
* In part (c) of #13, use the definition of ln x as 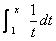 , not the definition you were taught in precalculus. , not the definition you were taught in precalculus.
(That is what you were supposed to have written for #12, also.) Calculator
keystrokes for entering this function in #13are as follows:
1. Press the WINDOW key.
2. Set Xmin=.001, Xmax=10, Xscl=1, Ymin=−10, Ymax=10, Yscl=1, Xres=5.
If you leave Xres=1, which is the default, your graph will take almost
forever to plot.
3. Press the “Y=” key in the upper left corner of your keypad.
4. Clear all function definitions. (Highlight each one and press CLEAR.)
5. For function Y1, Press MATH 9 1/T,T,1,X,.01 ENTER.
6. Press GRAPH and wait a while. If you forgot to set Xres=5 in step 2, you
will be waiting a long, long while.
7. Press Y= again and add a second function definition, Y2 = 1.
8. Press GRAPH 2nd TRACE 5 (the CALC intersection finder).
9. Press ENTER ENTER ENTER to choose Y1, Y2, and any
convenient starting point. After a long wait, you should find your point of
intersection.
|
|
|
T 11/23/010
|
HW due: Read §6-7; write
§6-6 #1-11 odd, 20, 21, and the two problems below.
Problem: Recall the compound
interest formula, 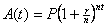 , where A(t) = amount on deposit in the account
after t years, r = annual interest rate expressed as a decimal (e.g., 0.03 if
the rate is 3%), n = number of
compoundings per year, and P = A0 = A(0) = principal amount, i.e., the amount deposited into the
account at time 0. Prove that , where A(t) = amount on deposit in the account
after t years, r = annual interest rate expressed as a decimal (e.g., 0.03 if
the rate is 3%), n = number of
compoundings per year, and P = A0 = A(0) = principal amount, i.e., the amount deposited into the
account at time 0. Prove that
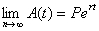 , which is the formula for exponential growth that you
learned in precalculus. , which is the formula for exponential growth that you
learned in precalculus.
Problem: Prove that if an
investment (or a population, or a quantity of matter, or whatever) is
experiencing exponential growth (decay) with periodic growth (decay) rate of w, where w is expressed in the form 100r,
then the doubling time (resp., half-life) is approximately 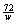 periods. This is
called the Rule of 72, and it is
essential knowledge if you plan to do anything with investments. periods. This is
called the Rule of 72, and it is
essential knowledge if you plan to do anything with investments.
Example: The population of the U.S. has a compound annual growth rate of
about r = 0.015, or 1.5%. We take w = 100r = 1.5 to get 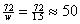 years as an estimate
of the time required for today’s population of about 309 million to double to
618 million. years as an estimate
of the time required for today’s population of about 309 million to double to
618 million.
Another example: Each hour, 10% of a radioactive quantity decays. Compute the
half-life.
Answer: Take w = 10 to get about
7 hours.
Another example: I have an investment that yields about 8%, before taking
taxes and inflation into account. About how long will it take to double in
nominal value?
Answer: Take w = 8 to get about
9 years.
|
|
|
W 11/24/010
|
No school.
|
|
|
Th 11/25/010
|
No school (Thanksgiving).
|
|
|
F 11/26/010
|
No school.
|
|
|
M 11/29/010
|
HW due: Read §§6-8 and 6-9;
write §6-7 #3-60 mo3. In #39, also state the equation of the line that is
tangent to f (x) at the point (−1, f
(−1)).
|
|
|
T 11/30/010
|
HW due: Write §6-8 #3-30
mo3, 32, and the problem below; prepare orally §6-9 #1-80 all (do not write
them out).
Problem: Use L’Hôpital’s Rule to
prove that 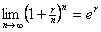 . .
|
|