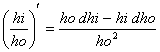|
F 10/1/010
|
No additional HW due.
However, please make sure that your previously assigned problems are well
organized and as complete as possible.
In class: Review of some commonly missed test problems, plus the beginning of
our chaos exploration. Form VI is on retreat today.
|
|
|
M 10/4/010
|
HW due: Read §3-4 and
prepare your calculator as directed below so that we are “ready to hit the
ground running” at the start of class. Approximately half of the people who
attended class last Friday have already accomplished this task, and you can
ask them for help or read your calculator manual if you get stuck.
(Voluminous TI-83/84 support is also available on the Internet.)
1. Choose a random number between 1.0 and 1.1. We used 1.02 _ _ _ _ _ _ _ ,
where the blanks represent the digits in Taylor’s phone number and the “2”
reminds us of the 202 area code. However, any similar number will do. You
should have 9 digits after the decimal point.
2. Store your random number into variable A.
3. Add 10−5 to your random number, and store the result into
B. Keystrokes: A+1E−5 STO B ENTER. Remember, you enter the
exponent by using the 2nd EE (“enter exponent”) command. The negative sign to
be used is the unary minus sign, which is the key immediately to the left of
the ENTER key, not the subtraction sign that is two keys above the ENTER key.
4. Recall value A to the “answer” buffer by keying in A ENTER.
5. Press the x2 key and
then press ENTER 11 times. This has the effect of iterating the squaring function 11 times. The result should be
very large, most likely 1020 or larger. Jot down your result.
6. Recall value B to the “answer” buffer by keying in B ENTER.
7. Press the x2 key and
then press ENTER 11 times. The result should be slightly larger than your
answer in step 5. Jot it down and compare. (In class, we noted that the
answers differed by only about 2%.)
8. Satisfy yourself that the first process is equivalent to the function 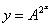 , where x denotes
the iteration number (0 gives starting value, 11 gives value after 11
iterations). Press MODE, if necessary, to make sure that your calculator is
in Func (function) mode, not Par, Pol, or Seq. Press the Y= key, and enter
the function that represents the iterated mapping as Y1=A^(2^X);
note that it would be an error to key in Y1=A^2^X, since your
calculator does not respect PEMDAS order of operations when exponents are
involved. Your calculator evaluates A^2^X as if it were (A^2)^X = A^(2X),
which is a programming bug. We simply have to be aware of this and work
around it. , where x denotes
the iteration number (0 gives starting value, 11 gives value after 11
iterations). Press MODE, if necessary, to make sure that your calculator is
in Func (function) mode, not Par, Pol, or Seq. Press the Y= key, and enter
the function that represents the iterated mapping as Y1=A^(2^X);
note that it would be an error to key in Y1=A^2^X, since your
calculator does not respect PEMDAS order of operations when exponents are
involved. Your calculator evaluates A^2^X as if it were (A^2)^X = A^(2X),
which is a programming bug. We simply have to be aware of this and work
around it.
9. Similarly, enter Y2=B^(2^X) for your second function.
10. Since Y1 and Y2 both increase by many orders of
magnitude between the 10th and 11th iterations, we need a way of graphing
them that preserves order while greatly compressing the vertical scale.
Somebody proposed using the LOG (common logarithm) or LN (natural logarithm)
button on the calculator for this purpose. Mr. Hansen arbitrarily chose LN.
Therefore, enter Y3 as Y3=LN(Y1) and Y4=LN(Y2).
The way to enter Y1 within the parentheses is to key in the
following four commands, which you should chant to yourself and memorize by
rote:
VARS
Y-VARS
Function
Y1
or, if you prefer, VARS Y-VARS 1 1 .
11. Turn the display of Y1 and Y2 off. Make sure Y3
and Y4 are turned on, and set the line thickness of Y4
to thick so that you will be able to see it when the graph is drawn.
12. Press WINDOW and make your settings as follows:
Xmin=0
Xmax=11
Xscl=1
Ymin= [doesn’t matter]
Ymax= [doesn’t matter]
Yscl=1E30
13. Press ZOOM 0 and wait patiently. After your calculator figures out how to
size the Y values, you should see Y3 plotted as a “J” curve,
followed soon afterward by the fat Y4 on top of it. Observe that
there is essentially no difference between the shape or behavior of the Y3
and Y4 curves.
14. Now, let us compare the natural logs of the two curves in a table. Press
2nd TBLSET (i.e., 2nd WINDOW) and make the following settings:
TblStart=0
 Tbl=1 Tbl=1
Indpnt: Auto
Depend: Auto
15. Press 2nd TABLE (i.e., 2nd GRAPH) and scroll down to see that at least
through the 11th or 12th iteration, there is no significant difference
between the two functions. The behavior of each iterated mapping (for that is
what these are called) is rather boring, certainly not chaotic.
16. In preparation for more interesting iterated mappings, we need to convert
to sequence mode. Press the MODE key and choose Seq.
17. Now, when you press the Y= key (do it now), you will see sequence
definitions instead of conventional function formula definitions. Below, when
we enter the letters u, v, or w in formulas, we will use the 2nd functions of
the numbers 7, 8, and 9. Important: Do not try to enter capital letters U, V,
or W. You will get nonsense if you do that.
18. Enter the following settings:
nMin=0
u(n)=u(n−1)2
u(nMin)=A
v(n)=v(n−1)2
v(nMin)=B
w(n)=
w(nMin)=
We will not use the w sequence for now. Use the CLEAR key if necessary to
clear those two settings.
Do you see how we have defined these sequences? The starting values, u(0) and
v(0), are set to constants A and B, respectively. After that, each iteration
(i.e., each entry in the sequence) is defined recursively as the square of
the previous one.
19. Return to table setup (2nd TBLSET) and set TblStart=0.
20. Press 2nd TABLE to see essentially the same behavior you saw in step 15.
The only difference is that now you are looking at the function values
themselves, not their natural logarithms.
21. (Optional step.) If you want to verify that we are getting the same
values as in step 15, you can hit MODE Func Y= and turn Y1 and Y2
on, Y3 and Y4 off. Then, when you press 2nd TABLE, you
should see exactly the same values that you saw a moment ago in step 20.
We did steps 1-20 on Friday. Did you follow all the steps? Good! Be sure to
leave your sequence definitions intact so that on Monday morning, I can press
MODE Seq Y= and verify instantly that everyone is “locked and loaded.” On
Monday, we will make tiny changes to the iterated function mappings
(sequences u and v), and suddenly, chaos will appear.
|
|
|
T 10/5/010
|
HW due: Read §3-5; write
§3-4 #1-21 all, 22, 24, 39.
In class: Substitute teacher and several videos on synchronization.
The first video is
28 minutes long, but I would like you to watch only the first 24 minutes.
(Stop the video at the 24:00 mark and go on to the second video.). Since the
first video is a little slow-paced, here are some study questions to
challenge you as you watch it:
1. Listen carefully at the 12:09 and 17:45 time markings. Would you change
the script slightly in those places?
2. At 5:14, Dr. Rockmore introduces the variable p, or more properly p(t), as the position of a planet
orbiting the earth. Clearly the domain for t is a subset of the real numbers. (Variable t tells us how much time has elapsed since some reference time.)
However, is p(t) a real-valued function, or is it a function whose range is
something other than real numbers? Argue with your classmates and see if you
can answer the question.
3. Suppose that p(t) is not a real number. What units
would be appropriate for the derivative, dp/dt?
The second
video is 22 minutes long, and you may need to listen to the last few
minutes at home. The Millennium Bridge segment duplicates some of the
information seen in the first video but is still interesting.
If you have time at the end, here is a short video (1
minute) of the Tacoma Narrows Bridge tearing itself apart in 1940.
If the substitute teacher needs help getting popup windows to display, I
trust that you can lend a hand.
Note-taking during the videos is encouraged, since if there is a quiz at a
later date, you will be permitted to use your notes.
|
|
|
W 10/6/010
|
HW due: Make sure that all
previously assigned problems, including the written problems in §3-4, are
complete and well organized.
|
|
|
Th 10/7/010
|
HW due: Read §§3-6 and 3-7;
write §3-5 #1, 2, 10.
|
|
|
F 10/8/010
|
No school (faculty
professional day).
|
|
|
M 10/11/010
|
No school (holiday).
|
|
|
T 10/12/010
|
HW due: Read §3-8; write
§3-6 #2, 3, 4, 7.
Challenge Problem
(optional, but highly recommended)
As you recall, a large majority of the students in class last Thursday had
successfully solved §3-5 #10, a problem that could be paraphrased as follows:
Suppose that 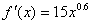 and f (0) = 50. Find f (10). and f (0) = 50. Find f (10).
The answer, 423.225 to the required AP accuracy, did not seem to baffle too
many people. Try the following entirely analogous problem:
Suppose that 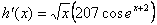 and h(0) = 30. Find h(1). and h(0) = 30. Find h(1).
The answer, from either the TI-83 or wolframalpha.com, is approximately
30.9968. The question is . . . can you get it?
|
|
|
W 10/13/010
|
HW due: Read §3-9; write
§3-8 #1, 2, 13, and the two problems below.
92. Suppose that 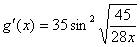 and g(1.3) = 11. Find g(4.9). and g(1.3) = 11. Find g(4.9).
93. Suppose that 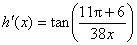 and h(1) = 2.818. Find h(1.2). and h(1) = 2.818. Find h(1.2).
|
|
|
Th 10/14/010
|
HW due: Review problems on
pp. 123-127 #R1abcd, R3d, R4abfgh, R5ab, R7d, R9abcd, T1-T6, T8-T17. For T17,
pretend that the equation for c(t) was not given, and try to re-derive
it.
If you do not finish all of these problems, then do as many as you can, and
finish the rest on Thursday night.
Here is an old sample test you can use for
practice. Question #10 is a nasty derivative involving multiple applications
of the Chain Rule, but as you can see on the solution
key, the answer has been verified with WolframAlpha.com. Please note that
you would not be expected to do anything that difficult on the real test.
|
|
|
F 10/15/010
|
Test (100 pts.) on Chapters 1-3 and all material
discussed in class, except that there will be no questions focusing solely on
the calculus of formal logic. Note,
however, that derived skills (such as knowing how to prove that a limit does
not exist) are still fair game.
|
|
|
M 10/18/010
|
HW due: Re-do your entire test from last Friday, and record how
long it takes you. You may confer with other students if you wish, but the
learning benefit is greater if you push yourself to do the best possible job
on your own before you break down and call somebody or look in the textbook.
The test may be re-graded for accuracy as a double (or triple) homework
assignment. Grammar, neatness, and legibility count.
You may find the sample test and solution key to be helpful resources.
|
|
|
T 10/19/010
|
HW due: Read this handout, §4-2, and §4-3;
write §4-2 #1-29 odd. Also read the following two-part memory aid for the
quotient rule, passed down by calculus teachers since time immemorial:
1. Start and end with the “ho.” [We say “hi” and “ho” instead of “high” and
“low” just to be silly. As you should know, silly things are easier to
remember.]
2. 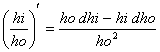
Pronunciation: “Hodie hi minus hidie ho, all over ho squared.”
|
|
|
W 10/20/010
|
HW due: Read §4-4; write
§4-3 #1-29 odd, but do only as many as you need to do to master the
techniques. A full 35-minute dose is not required tonight. If in doubt,
remember that more practice is generally better, but be sure to get the sleep
you need as well. At your age, you need (cough, cough) about 9 hours per
night. It’s true! Try getting some extra sleep and see if it improves your
mental sharpness.
|
|
|
Th 10/21/010
|
HW due: Read §4-5 and
memorize the green boxes on p. 142 and p. 150. There may be a quiz, but
because of the choral festival in the Cathedral Wednesday night, there is no
additional written work due.
|
|
|
F 10/22/010
|
HW due: Read §4-6 (omitting
the proof on p. 154 for now); prepare §4-6 #1-12 all for oral presentation;
write pp. 173-174 #R1ab, R3b (using PR and CR, not def. of derivative),
R4abcd, R5a, R6abcd, and the problem below.
999. Use the green box on p. 153, or any other clear procedure, to prove that
the derivative of ln x, the natural
log function that you learned about in previous classes, equals x−1. You may use as a
lemma the fact that
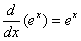 . .
|
|
|
M 10/25/010
|
Test (100 pts.), cumulative through §4-6. You will not be required, for now, to prove that differentiability
implies continuity (proof on p. 154), but you are required to know the
implication and its contrapositive. The only new proof for which you are held
responsible is to prove QR using PR and CR as lemmas.
Green boxes on p. 142, p. 148, and p. 153 should be memorized. Note that
there are two typos in the green box on p. 148; corrections were announced in
class. The box on p. 153 need not be memorized, actually, if you remember the
“thinking about what f is doing at
point (x, y)” approach that we used in class last Thursday.
|
|
|
T 10/26/010
|
HW due: Read §4-7; write
§4-7 #2abcde. Note that part (e) is on the next page.
|
|
|
W 10/27/010
|
HW due: Read §4-8; write
§4-7 #10, 13. We will do problems from §4-8 in class before we do any at
home.
|
|
|
Th 10/28/010
|
HW due: Read pp. 180-181;
write §5-1 #1-7 all.
|
|
|
F 10/29/010
|
End of Q1. All Mathcross puzzles and any other graded
items must be submitted by 3:00 p.m. today.
HW due: Read §5-2; prepare (orally) §5-2 #1-16 all; write §4-8 #1-21 odd.
Please check your answers for §4-8 either in the back of the book or on
wolframalpha.com.
|
|