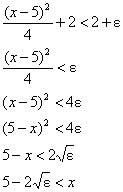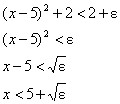|
W 9/8/010
|
First day of class.
|
|
|
Th 9/9/010
|
HW due: Watch video topics #3C and #4 (Greek and Roman alphabets for
the calculus) and read §1-1. There will be a quiz.
|
|
|
F 9/10/010
|
HW due: Read §1-2; prepare
#Q1-Q10 and #1-10 for oral presentation (written notes recommended), and
write §1-2 #13, 14, and the exercise below. Follow the formatting
requirements. A 3-ring binder is recommended and will be required
beginning next Monday.
When you are preparing #1-10 on p. 11 for oral presentation, assume that the
horizontal and vertical scales are equal. (Note: On the AP exam, you should never assume that to be case.)
Also be prepared to estimate the value of the derivative function at the
marked x-values. An example of what
I would expect for #2 is prepared for you below, but writing out #Q1-Q10 and
#1-10 is optional. We will do these problems orally.
2. f (x) is increasing at x =
a; the rate of increase is “fast”
since 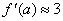
f (x) is decreasing at x = b; the rate of decrease is “slow” since 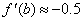
Exercise: Sketch a graph of your
position function, s(t), with t on the horizontal axis, for your morning commute to class.
Label a few points of interest on the horizontal axis. Then show the
derivative function, 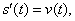 on a separate set of
axes lined up directly below. Don’t put too much detail into it (for example,
you could spend hours adding every traffic light and street crossing, and
that would be overkill). Allocate about 5-6 minutes to this task. Indicate
units in parentheses. For example, write “(meters/sec.)” or “(mph)” or
something similar for your v(t) sketch. on a separate set of
axes lined up directly below. Don’t put too much detail into it (for example,
you could spend hours adding every traffic light and street crossing, and
that would be overkill). Allocate about 5-6 minutes to this task. Indicate
units in parentheses. For example, write “(meters/sec.)” or “(mph)” or
something similar for your v(t) sketch.
|
|
|
M 9/13/010
|
HW due:
1. Purchase a 3-ring binder if you have not already done so. Beginning today,
a 3-ring binder, a pencil, a TI-83 or TI-84 calculator, and your textbook are
required equipment every day. Keep all homework and reading notes in your
3-ring binder. I recommend keeping reading notes and homework on the same
sheet of paper, but some students prefer to keep all of their reading notes
in one separate place. Either way is acceptable.
2. Read §1-3 (reading notes required, as always) and write §1-3 #1-4 all.
(Include a sketch of each graph. Graph paper is not required.) You can check
your work by using the fnInt function (MATH 9) on your calculator. The syntax
is fnInt(function,X,start,end) where “function” denotes any function of x, X denotes the letter X (entered by
pressing the “X,T,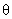 ,n” key near the
upper left of your keypad), “start” = left endpoint, and “end” = right
endpoint. For example, here are the keystrokes to check the answer to #1(a): ,n” key near the
upper left of your keypad), “start” = left endpoint, and “end” = right
endpoint. For example, here are the keystrokes to check the answer to #1(a):
MATH 9 (-) .1X^2+7,X,0,5 ENTER
The AP standard accuracy requirement is a minimum of 3 decimal places after
the decimal point. You would write your answer as 30.833, but of
course your estimate by counting squares would probably be more like 30 or
31. Be sure to count the squares as part of your learning adventure!
3. Memorize the following definition of limit:
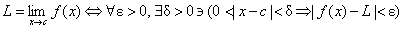
The meaning of the cryptic symbols can be found at www.StudyOfPatterns.com/abbrevs2.htm.
The definition is difficult and will take several days to learn. If you are
quizzed on it on Monday, a partially correct recollection will be acceptable
for full credit.
|
|
|
T 9/14/010
|
HW due:
1. The symbols 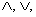 and ~ mean “and,” “or,”
and “not,” respectively. The same abbreviations
page you looked at for yesterday’s assignment has those and many others
listed. A conjunction involving “and” is true iff both parts are true, and a
disjunction involving “or” is false iff both parts are false. As we discussed
in class yesterday, the conditional statement and ~ mean “and,” “or,”
and “not,” respectively. The same abbreviations
page you looked at for yesterday’s assignment has those and many others
listed. A conjunction involving “and” is true iff both parts are true, and a
disjunction involving “or” is false iff both parts are false. As we discussed
in class yesterday, the conditional statement 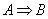 is false iff (A is
true and B is false). Below is a “truth table proof” showing that is false iff (A is
true and B is false). Below is a “truth table proof” showing that 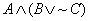 is equivalent to is equivalent to 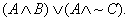 Study the proof. The
objective is to achieve all TRUE (value of 1) in the final column. When
listing permutations of possible truth values for A, B, and C, it is helpful
to list them in the systematic fashion shown. Study the proof. The
objective is to achieve all TRUE (value of 1) in the final column. When
listing permutations of possible truth values for A, B, and C, it is helpful
to list them in the systematic fashion shown.
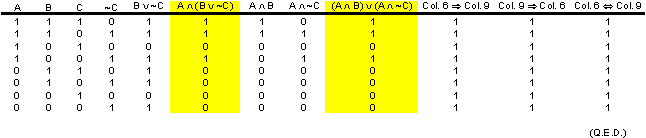
2. When determining whether a theorem involving atomic statements and logical
symbols is TRUE, we use a truth table, and we check whether the final column
is true for all possible values of the atomic statements. Make a truth table
to prove that 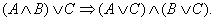 Use the same
systematic style as shown in the example for #1 above. Use the same
systematic style as shown in the example for #1 above.
3. Read §§1-4 and 1-5, plus §1-5 #15 and its solution on p. 669. (Reading
notes are required, as always.)
4. Write §1-5 #16.
|
|
|
W 9/15/010
|
HW due: Read §§2-1 and 2-2;
then write the answers to the following questions.
1. Yesterday I wrote on the board words similar to the following: “The limit,
if the limit exists, is the unique number that function f can be kept arbitrarily close to whenever x is within a sufficiently small punctured neighborhood of the
fixed x-value in question.”
(a) What letter do we normally give to “the fixed x-value in question”?
(b) What does the phrase “arbitrarily close” mean? Write a sentence or two.
(c) What does the phrase “sufficiently small” mean? Write a sentence or two.
(d) Is it acceptable to switch the phrases “arbitrarily close” and
“sufficiently small”? Explain.
2. The symbol for an AND gate is 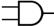 (2 inputs entering from the left, 1 output
exiting to the right), and the symbol for a NAND gate is almost identical
except for a circle on the right that indicates inversion of the output: (2 inputs entering from the left, 1 output
exiting to the right), and the symbol for a NAND gate is almost identical
except for a circle on the right that indicates inversion of the output: 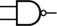 . Show
how it is possible to connect a group of 3 NANDs in some fashion so that,
altogether, their overall behavior is the same as . Show
how it is possible to connect a group of 3 NANDs in some fashion so that,
altogether, their overall behavior is the same as
(a) a single AND gate,
(b) a single OR gate.
The answers are on Wikipedia (of course, as almost everything is), but see if
you can solve these puzzles by working on your own. Recall that in class, we
saw how a NOT can be created from a NAND gate as follows:
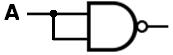
Observe, please, that if A = 1, then 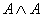 = 1, so that A NAND
A = 0, and if A = 0, then = 1, so that A NAND
A = 0, and if A = 0, then 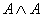 = 0, so that A NAND
A = 1. But either way, the output equals the negation of A. Therefore, this
NAND gate, with A driving both of the inputs, functions exactly like a NOT
gate. = 0, so that A NAND
A = 1. But either way, the output equals the negation of A. Therefore, this
NAND gate, with A driving both of the inputs, functions exactly like a NOT
gate.
|
|
|
Th 9/16/010
|
HW due:
1. Carefully explain the fallacy in the “proof” below.
Theorem: A ham sandwich is better
than complete happiness.
Proof: Nothing (N) is better than
complete happiness (C).
But if you were hungry, or even if you weren’t particularly hungry, a ham
sandwich (H) would be better than nothing.
Therefore, since H > N and N > C, we have H > C. Thus a ham sandwich
is better than complete happiness. 
2. Carefully explain the fallacy in the mathematical induction proof below.
Theorem: All men are essentially
bald.
Proof: Let B(n) denote the
statement that a man with n hairs
on his head is essentially bald.
Basis case: A man with 1 hair on his head is essentially bald. Thus B(1) is true by inspection.
Induction step: We seek to show that for any natural number k, B(k) implies B(k + 1). Clearly this
is true, since if there were a man whom we called essentially bald, adding
one hair to his head would not change our view of him as being essentially
bald. Therefore, 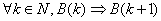 . .
By mathematical induction, B(k) is true for any natural number.
Therefore, every man is essentially bald. 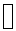
3. Learn (do not prove) the following rules of the first-order predicate
calculus:
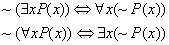
For each statement, translate it into plain English, and then give an example
from real life to suggest that it makes sense. An example for the first one
(you can’t use this; you’ll need one of your own) is that saying “It is not
the case that there exists a St. Albans student who is grouchy” is equivalent
to saying “For any St. Albans student, that student is not grouchy.”
4. (Optional, but recommended.) Use a truth table to prove that 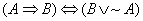 . .
|
|
|
F 9/17/010
|
Catch-up day (no additional
HW due; use the time to get caught up). A quiz on recent class discussions is
likely.
|
|
|
M 9/20/010
|
HW due: Read §2-3; write
§2-2 #1-13 all. Problems #3 and #11 are done for you as examples below, with much
more explanation than you would need to include in your own work. (No
explanation is expected for #1-6, and terse explanations will suffice for the
rest of the problems.)
3. 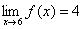
Let y = f (x).
An 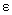 band of 0.7 means
that the y-values must be kept
within the open interval (3.3, 4.7). It appears that a domain of x-values from about 5.2 to 6.6 will
map, under f, to the desired band
of (3.3, 4.7) for y-values. But
note: f is steeper on the right
than on the left. Therefore, the controlling feature will be the 6.6 on the
right, not the 5.2 on the left. Thus a band of 0.7 means
that the y-values must be kept
within the open interval (3.3, 4.7). It appears that a domain of x-values from about 5.2 to 6.6 will
map, under f, to the desired band
of (3.3, 4.7) for y-values. But
note: f is steeper on the right
than on the left. Therefore, the controlling feature will be the 6.6 on the
right, not the 5.2 on the left. Thus a 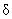 value of 0.8, which
would work on the left side of x = 6,
will be too wide on the right. On the right side of x = 6, it is not possible to go more than about 0.6 units before
violating the value of 0.8, which
would work on the left side of x = 6,
will be too wide on the right. On the right side of x = 6, it is not possible to go more than about 0.6 units before
violating the 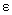 band for y-values. By taking band for y-values. By taking 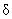 to be the minimum of
0.8 and 0.6, namely 0.6, we can find a punctured to be the minimum of
0.8 and 0.6, namely 0.6, we can find a punctured 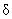 -neighborhood of 6 that works on both sides. Answer: -neighborhood of 6 that works on both sides. Answer: 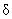 = 0.6 should
suffice. = 0.6 should
suffice.
11.(a) [See illustration in #5.]
(b) 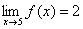 [not by inspection,
but rather by plugging x = 2 into
both parts of the piecewise definition] [not by inspection,
but rather by plugging x = 2 into
both parts of the piecewise definition]
(c) On calculator, plot Y1 = 0.25(x − 5)2 + 2, Y2
= (x − 5)2 + 2, Y3
= 2.3. The points of intersection [found by calc., using 2nd TRACE 5] are
approximately (3.904555, 2.3) and (5.547723, 2.3). Those points suggest
candidate values for 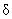 of about 1.0954
(looking to the left of x = 5) and
about 0.5477 (looking to the right of x
= 5). We must choose the minimum of these in order to guarantee a punctured of about 1.0954
(looking to the left of x = 5) and
about 0.5477 (looking to the right of x
= 5). We must choose the minimum of these in order to guarantee a punctured 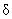 -neighborhood of 5 that works on both sides. Answer: -neighborhood of 5 that works on both sides. Answer: 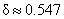 . [Also note that we must always round down in problems of this sort in order to avoid violating the . [Also note that we must always round down in problems of this sort in order to avoid violating the 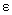 band. The AP exam standard
is a minimum of 3 decimal places after the decimal point. An answer of 0.548
would satisfy proper AP format but would be incorrect in this instance.] band. The AP exam standard
is a minimum of 3 decimal places after the decimal point. An answer of 0.548
would satisfy proper AP format but would be incorrect in this instance.]
(d) First, solve the inequality for the left side of
the function definition:
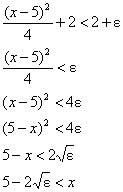
This suggests a 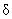 value of value of 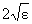 on the left. [We
know this is largely a waste of time, since the function is not changing as
rapidly on the left as on the right. However, the exercise is useful in order
to practice our algebra. Note especially the substitution of (5 − x)2 for (x − 5)2, which is a
useful trick to make it possible to take square roots without worrying about
flipping the signs of the inequality. Remember, 5 − x is positive for x values on the left side of 5.] on the left. [We
know this is largely a waste of time, since the function is not changing as
rapidly on the left as on the right. However, the exercise is useful in order
to practice our algebra. Note especially the substitution of (5 − x)2 for (x − 5)2, which is a
useful trick to make it possible to take square roots without worrying about
flipping the signs of the inequality. Remember, 5 − x is positive for x values on the left side of 5.]
Second, solve the inequality for
the right side of the function definition:
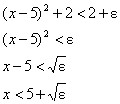
. . . which suggests a 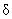 value of value of 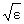 on the right. on the right.
Finally, take 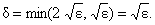 [This is how we
prove limits rigorously: by finding an acceptable value for [This is how we
prove limits rigorously: by finding an acceptable value for 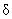 that depends on
nothing other than the knowledge of x
and that depends on
nothing other than the knowledge of x
and 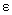 . Since . Since 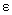 > 0 can be
assumed as given, we have demonstrated wlog a valid method for producing > 0 can be
assumed as given, we have demonstrated wlog a valid method for producing 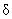 > 0.] > 0.]
|
|
|
T 9/21/010
|
HW due:
1. Since yesterday’s assignment was hard, I would like you to spend some time
finishing, polishing, and reviewing it.
2. Then, write §2-3 #20 and parts (a) and (b) of the additional problem
below.
26. We learned the technical definition of limit, namely
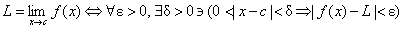 . .
(a) What, exactly, does it mean for 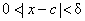 to imply to imply 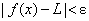 ? Write your answer using
the notation ? Write your answer using
the notation 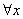 in combination with
interval or punctured interval notation. Recall, please, that the punctured
open interval from in combination with
interval or punctured interval notation. Recall, please, that the punctured
open interval from 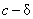 to to 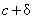 can be denoted as
follows: can be denoted as
follows:
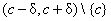
(b) Confer with a classmate to make sure you both have the correct answer to
part (a) before proceeding. Then rewrite the formal definition of limit using
4 quantifiers instead of 2. You should have 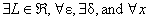 all as part of your
definition. all as part of your
definition.
(c) Apply a multi-step negation procedure to your answer in (b), in a manner
similar to what we did in class yesterday, to find out exactly what it means
for there to be no limit L for
function f (x) as x approaches c. (We use the notation DNE to
indicate that the limit “does not exist.”) Hint: Before negating, you have something like this:
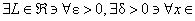 . . . [etc.] . . . [etc.]
After negating, you will have
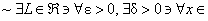 . . . [etc.], which
must have the “~” sign repeatedly passed inside until you boil the expression
all the way down to its essence. . . . [etc.], which
must have the “~” sign repeatedly passed inside until you boil the expression
all the way down to its essence.
|
|
|
W 9/22/010
|
HW due: Write #26(c) from
yesterday, read §2-4; write §2-4 #21-42 mo3. Prepare all of the problems
#21-42 for oral presentation in class, but you need to write out only the
multiples of 3 (#21, 24, 27, 30, 33, 36, 39, 42).
|
|
|
Th 9/23/010
|
HW due: Read §2-5; write
§2-4 #65, 66, 68, 70.
|
|
|
F 9/24/010
|
HW due: Read §2-6; write
§2-5 #1-5 all, 7. Also read and decipher the following symbolic version of
IVT:
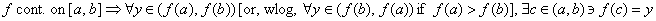
|
|
|
M 9/27/010
|
HW due: As announced in
class, you are to answer questions #4-20 in §2-4, except for function 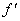 instead of instead of 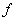 . (The first few are done below as examples for you. They are
harder than they look.) Then, write §2-6 #4, 5, 7. . (The first few are done below as examples for you. They are
harder than they look.) Then, write §2-6 #4, 5, 7.
If you have additional time, begin preparing for tomorrow’s test by working a
selection of review problems (pp. 71-73) and practice test problems (pp.
74-76). You may also look at an
actual Mr. Hansen test from 2008 to get an idea of the difficulty level
you can expect tomorrow. Tomorrow’s test will have fewer questions on
derivatives and more questions on formal logic.
Solutions for §2-4 #1-3:
1.(a) 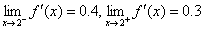
Note:
Also state the left- and right-hand derivatives, which are 0.4 and DNE
(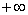 ), respectively. ), respectively.
(b) 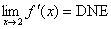
(c) 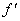 has a jump
discontinuity at x = 2 has a jump
discontinuity at x = 2
2.(a) 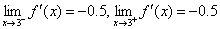
Note:
Also state the left- and right-hand derivatives, which are both DNE
since f (3) does not exist.
[Left- and right-hand derivative
definitions require the existence of f
(c), which is f (3) here. Just as the derivative
of function f at x = c is defined as the (2-sided) limit of
a difference quotient involving f (c), the left-hand
derivative is defined as 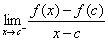 . Similarly, the right-hand derivative is . Similarly, the right-hand derivative is 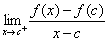 .] .]
(b) 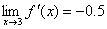
(c) Even though 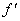 has a 2-sided limit
at x = 3, continuity fails since has a 2-sided limit
at x = 3, continuity fails since 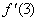 does not exist. The
discontinuity is removable. does not exist. The
discontinuity is removable.
3.(a) 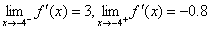
Note:
Also state the left- and right-hand derivatives, which in this case [unlike
what we saw in problems #1
and #2] are the same as the left- and
right-hand limits of 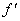 , namely 3 and −0.8, respectively. , namely 3 and −0.8, respectively.
(b) 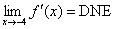
(c) 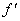 has a jump
discontinuity at x = 4 has a jump
discontinuity at x = 4
Note:
It is true that f has a cusp at x = 4. However, 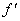 has a jump
discontinuity there. has a jump
discontinuity there.
|
|
|
T 9/28/010
|
Test (100 pts.) on Chapters 1 and 2 and all
classroom discussion, including the names Newton, Leibniz, Turing, and Gödel,
and the calculus of formal logic.
Thanks to Taylor B., an answer key to
the practice test is now available.
|
|
|
W 9/29/010
|
No additional HW due, but
older assignments may be spot-checked.
|
|
|
Th 9/30/010
|
HW due: Read §§3-2 and 3-3,
including the green box at the top of p. 84; write §3-2 #15bcde, 17, §3-3 #7,
and the additional questions below.
115e. Reword the statement in #15e on p. 82 so that it is rigorously correct.
Hint: Consider the function y = x1/3, which has local linearity at the origin even
though the derivative is DNE when x
= 0.
116a. Demonstrate that you understand the difference between 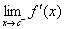 and the left-hand
derivative of f at x = c by writing a few sentences in your own words (with correct
grammar, spelling, and punctuation). and the left-hand
derivative of f at x = c by writing a few sentences in your own words (with correct
grammar, spelling, and punctuation).
b. Under what circumstances does 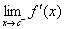 equal the left-hand
derivative of f at x = c? equal the left-hand
derivative of f at x = c?
In class: Surprise visit from 14-year-old Davidson Fellow, Meredith Lehmann
of La Jolla, California.
|
|