AP Statistics / Mr. Hansen
2/12/2001

Name: _________________________

Suppose that 40% of the people in a population of size N are supporters of George W. Bush. If we select an SRS of n people from the population, what is the probability that more than 50% of the people in our sample are George W. Bush supporters?

1.

Answer the question under the assumption that n = 5, N = 10.

2.

Answer the question under the assumption that n = 5, N = 70.

3.

Answer the question under the assumption that n = 15, N = 1000.

4.

Answer the question under the assumption that n = 30, N = 1000.

5.

Answer the question under the assumption that n = 3500, N = 60,000,000.

ANSWERS (no fair peeking until you have tried to solve all the problems!)

In all cases, let X = # of "Dubya" supporters in the sample, and let .

1.

The population is too small to assume "nearly independent" trials, so we have to puzzle this out the hard way. (The technical name for this distribution is hypergeometric, although your book doesn’t use this term.) Note that there are 4 Dubya supporters and 6 non-Dubya supporters in the population. Each time we must choose some from the subgroup of 4 and some from the subgroup of 6.

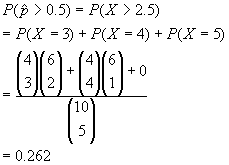
2.

You can proceed as in #1 (which is hard), or you can use the simplifying assumption that the trials are nearly independent since N ³ 10n. The exact answer (not recommended unless you are a glutton for punishment) is
P(ˆp > 0.5) = P(X > 2.5)
= P(X = 3) + P(X = 4) + P(X = 5)
= [(₂₈C₃)(₄₂C₂) + (₂₈C₄)(₄₂C₁) + (₂₈C₅)(₄₂C₀)] / ₇₀C₅
= 0.312

Luckily, you would never be expected to do this much heavy lifting on the AP in a situation like this. Using the simplifying assumption and treating this as a binomial case, we have

P(X > 2.5) = 1 – P(X £ 2.5) = 1 – 0.68256 = 0.317,

which is acceptably close to the true answer. (Note: The value 0.68256 is computed as binomcdf(5,0.4,2), although you would of course never show the calculator notation on your paper.)

For full credit, you should say that trials are nearly independent since 70 ³ 10n = 50, and P(ˆp > 0.5) = P(X > 2.5) = 1 – P(X £ 2.5) = 1 – 0.68256 = 0.317 by calc. (binomial).

3.

Since N is much larger than 10n, use binomial simplification:

P(ˆp > 0.5) = P(X > 7.5) = 1 – P(X £ 7.5) = 1 – 0.787 = 0.213.

(The exact answer, in case you are curious, can be computed after much tedium to be 0.211. Moral of the story: Use the binomial simplification when you can!)

4.

Here, you could use the binomial simplification since N ³ 10n, and you would get

P(ˆp > 0.5) = P(X > 15) = 1 – P(X £ 15) = 1 – 0.903 = 0.097.

However, since np = 30(0.4) = 12 ³ 10 and nq = 30(0.6) = 18 ³ 10, we could also use the normal approximation. In the normal approximation of the sampling distribution of ˆp, we have mean m_ˆp = p = 0.4 and s.d. s_ˆp = Ö(pq/n) = Ö[(0.4)(0.6)/30] = 0.0894427191. Therefore,

P(ˆp > 0.5) = [area from 0.5 to +¥ under the N(0.4, 0.0894427191) distrib.] = 0.132.

This approximation is considered acceptable for the AP exam, provided you justify use of the normal approximation by showing your work and checking the following:

N = 1000 ³ 10n = 300
np = 30(0.4) = 12 ³ 10
nq = 30(0.6) = 18 ³ 10

Note: If you are disturbed by the rather large percentage error in this answer, you may be interested to know that there is a technique (not required for AP exam) called the continuity correction of the normal approximation. Basically, the idea is that you average the result you got above, namely normalcdf(0.5, 999999, 0.4, 0.0894427191) = 0.131776284, with normalcdf(0.533333, 999999, 0.4, 0.0894427191) = 0.0680190835. The average, namely 0.0999, is very close to the binomial answer of 0.097 or the tedious hypergeometric answer of 0.094. And where does 0.533333 come from? That is simply the proportion of successes you would have with the next higher count, namely 16 out of 30. Since by common sense P(X > 15) does not seem to match either P(X ³ 15) or P(X ³ 16), we "split the difference."

Note: If the last paragraph made no sense to you, please ignore it. On the AP exam, it matters not whether you include or omit endpoints in normal distributions, and the continuity correction is not expected.

5.

Here, if you have a TI-83, you have no choice but to use the normal approximation, since only the TI-83 PLUS will accommodate n ³ 1000 in binomial distributions.

Method 1 (not possible for TI-83 "classic"): Trials are nearly independent since N is much larger than 10n.
P(ˆp > 0.5) = P(X > 1750) = 1 – P(X £ 1750) = 1 – 1 = 0.

Note: Technically speaking, the binomial probability P(X £ 1750) does not equal 1, but the difference is too small to be shown by your calculator. This computational error is called underflow.

Method 2 (workable for either TI-83 "classic" or TI-83 PLUS): Trials are nearly independent since N >> 10n. Normal approx. OK since np and nq >> 10.
Since the sampling distr. of ˆp has s_ˆp = Ö(pq/n) = Ö[(0.4)(0.6)/3500] = 0.0082807867, the desired value of 0.5 is many s.d.’s above 0.4 (more than 12 s.d.’s, if you must know). There is basically no chance of getting a value for ˆp that high! (My calculator gives 7.281 · 10^–34, but you would be forgiven for writing 0.)