1.
A random variable X that follows a _binomial_ distribution, abbreviated B( _n_ , _p_ ), gives the number of _successes_ when exactly n _independent_ trials are made, where each trial has only __2__ possible outcomes, called "_success_" and "_failure_." The probability of success on each trial is a fixed constant __p__ , and the probability of failure on each trial is a fixed value 1 – p, often abbreviated __q__ .
2.
The probability of exactly a successes (a £ n) in the B(n, p) distribution is given by the formula _P(X = a)_ = nCa · paqn – a __(where X = # of successes in n independent trials)__.
3.
The mean (expected value) of a binomial random variable X is _____np_____ if X follows the B(n, p) distribution. The standard deviation of X is ____(npq)1/2__________ .
4.
To find P(X = a) for a binomial distribution, use the following calculator keystrokes:
2nd DISTR 0 (n,p,a) ENTER, i.e., binompdf(n, p, a)
On AP exam, show the work as P(X = a) = nCa · paqn – a = [plug-in] = [answer] by calc.
5.
To find P(X £ a) for a binomial distribution, use the following calculator keystrokes:
2nd DISTR A (n,p,a) ENTER, i.e., binomcdf(n, p, a)
On AP exam, show the work as P(X £ a) =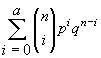 
= [plug-in and show a few terms] = [answer] by calc.
6.
If a fair coin is flipped 150 times, compute each of the following:
Let X = # of heads when fair coin is flipped 150 times. [Must state for full credit.]
Note: p = q = 0.5 in this case.
The solutions below indicate the work you would be expected to show for full credit.
(a)
the probability that there are exactly 75 heads
(k = 75)
P(X = 75) = nCk · pkqn – k = 150C75 · 0.5750.575 = 0.065
(b)
- the probability that there are at least 75 heads
(k = 75)
P(X £ 75) =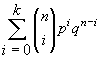
= 150C0 · 0.500.5150 + 150C1 · 0.510.5149 +150C2 · 0.520.5148 + . . . = 0.5325 by calc.
(c)
the probability that there are 75 or 76 heads
(k = 75, j = 76)
P(X = 75 or X = 76) = nCk · pkqn – k + nCj · pjqn – j = 150C75 · 0.5750.575 + 150C76 · 0.5760.574 = 0.129 by calc.
(d)
the expected number of heads
mX = np = 150(0.5) = 75
(e)
- the standard deviation in the number of heads that occur
sX = (npq)1/2 = (150 · 0.5 · 0.5)1/2 = 6.124
(f)
the probability that there are more than 95 heads
P(X > 95) = 1 – P(X £
95) = 1 – 0.99962 (by calc.) = 0.00038