Name: __________________________________
Students to whom you gave help: ________________________
Sketchpad Lab VI
1. Open Geometer's Sketchpad to a New Sketch
2. Place 4 points on your sketch. Label them A, B, C, D.
3. Construct quadrilateral ABCD.
4. Move the points around so that ABCD is a convex quadrilateral which is not a parallelogram, kite or trapezoid.
5. What are the lengths of the sides of your quadrilateral?
AB = _________ BC = ____________ CD = _________ AD = ___________
6. Find the measure of
Ð ABC. _________7. Construct the midpoints of the sides of your quadrilateral ABCD. Label them so that the midpoint of
sAB is M, the midpoint of sBC is N, the midpoint of sCD is P and the midpoint of sAD is Q.8. Construct quadrilateral MNPQ.
9. What are the lengths of the sides of this new quadrilateral?
MN = _________ NP = ___________ PQ = ____________ QM = ___________
10. What are the measures of the angles of this new quadrilateral?
Ð
MNP = _________ Ð NPQ= _________ Ð PQM = _________ Ð QMN = _________
Conjecture I: If the midpoints of the sides of a convex quadrilateral are joined in order, the most descriptive name for the quadrilateral formed is:
11. Move points A, B, C and D so that ABCD is a kite, but not a parallelogram.
12. Now what are the lengths of the sides of MNPQ?
MN = _________ NP = ___________ PQ = ____________ QM = ___________
13. What are the measures of the angles of MNPQ?
Ð
MNP = _________ Ð NPQ= _________ Ð PQM = _________ Ð QMN = _________Conjecture II: If the midpoints of the sides of a kite are joined in order, the most descriptive name for the quadrilateral formed is:
14. Move points A, B, C and D so that ABCD is a rectangle, but not a square.
15. Now what are the lengths of the sides of MNPQ?
MN = _________ NP = ___________ PQ = ____________ QM = ___________
16. What are the measures of the angles of MNPQ?
Ð
MNP = _________ Ð NPQ= _________ Ð PQM = _________ Ð QMN = _________Conjecture III: If the midpoints of the sides of a rectangle are joined in order, the most descriptive name for the quadrilateral formed is:
17. Close, but do not save this sketch. Open a new sketch.
18. Place two points on the sketch and construct the segment joining them.
19. Select one of the points, highlight it and the segment. Construct a perpendicular line.
20. Use "Construct Point on Object" to place another point on the perpendicular line.
21. Highlight all three points, and use "Construct Segment" to make a right triangle.
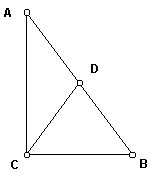
22. Label the vertices of the right triangle A, B, and C, with C the vertex at the right angle.
23. Construct the midpoint of the hypotenuse, and label it D, as shown. Construct the median CD.
24. Measure the lengths AD, DB, and CD. Drag points around to change the size and shape of your right triangle.

Conjecture IV
: The median to the hypotenuse in a right triangle is