Name 1: ____________________________________
Name 2: ____________________________________
Sketchpad Lab I
Directions:
You will need a pencil to write some answers on the lab report. Be sure to save your work where indicated. If you get stuck, please confer quietly with the people on your right and left. Try to learn from your friends if possible. If several of you get stuck in the same place, raise your hand for help.
Exercise 1.
1. Open Geometer's Sketchpad, and open a new sketch.
2. Using the point tool, place two points on your sketch.
3. Using the label tool (little hand) name your points A and B.
4. Select both points, using the shift key to do so.
5. Go to the CONSTRUCT menu and construct a line segment connecting your two points.
6. Select the points A and B, and go to the MEASURE menu. Choose DISTANCE.
7. What is the length of your segment? AB = _____________.
8. Select the segment. Go to the DISPLAY menu. Hide the segment.
9. Go to the tool bar at the left, and change from the segment icon to the ray icon.
Figure out how to construct the ray rAB through your points A and B.
Call me over to see your ray rAB.
Keep this sketch. We will use ray rAB for the next exercise.
Write directions below so that another person could construct ray rAB if the points A and B were already on the sketch.
Exercise 2. Three ways to construct a 45˚ angle.
Use the sketch and ray AB from exercise 1.
Method 1: To Construct a 45˚ angle.
1. Select point A. Go to TRANSFORM and choose MARK CENTER A.
2. Select ray AB. Go to TRANSFORM, ROTATE. Type 45 for the number of degrees of rotation.
3. Place and label points so that we may correctly call the angle Ð
CAB.
After you have shown me your angle, hide ray rAC and point C.
Method 2: To Construct a 45˚ angle.
1. Select point A. Go to TRANSFORM and choose MARK CENTER A..
2. Select ray AB. Go to TRANSFORM, ROTATE.. Type 90 for the number of degrees of rotation.
3. Place and label points so that we may correctly call the right angle Ð
DAB.
4. Select points D, A and B in correct order for naming the angle.
Go to CONSTRUCT and select ANGLE BISECTOR.
5. Hide ray rAD and point D.
6. Label points so that your 45˚ angle may be called Ð
EAB
After you have shown me your angle, hide ray rAE and point E.
Method 3: To construct a 45˚ angle.
1. Select point A and ray rAB.
Go to CONSTRUCT and choose PERPENDICULAR LINE.
2. Place a point on the line and call it G.
3. Bisect Ð
GAB. Place and label a point so that a 45˚ angle may correctly be called Ð
KAB.
4. Select and hide the line which is perpendicular to ray rAB, and any points not on that angle.
When you are sure that you understand all three methods of constructing the 45˚ angle, close and do not save this sketch. Open a new sketch for the next exercise.
Exercise 3.
1. Construct right angle PQR with PQ @
QR.
2. Construct segment sPR so that you have DPQR, with one right angle.
3. Select points Q, P, R, in correct order to name Ð
QPR.
4. Go to MEASURE. Choose angle. What is the measure of Ð
QPR? ________
5. Measure Ð
QRP. What is the measure of Ð
QRP? ___________
6. Move point P to change the shape of your triangle.
What are the measures of Ð
QPR and Ð
QRP now?
Ð
QPR = _____________ Ð
QRP = ______________
Try to find an interesting conjecture about these angles.
Conjecture: In a triangle which has one right angle, the other two angles are
______________________________________________________________.
Close this sketch and do not save it. Open a new sketch for the next exercise.
Exercise 4.
1. Place a circle on the sketch and place three more points on that circle.
label those points M, A, T, H, in consecutive order.
2. Construct segments so that you have a quadrilateral named MATH.
Hide the center of the circle. Your drawing should resemble the following:
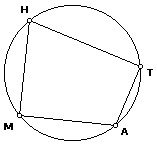
3. Measure these four angles and write their measures:
Ð
MHT = _____________ Ð
HTA = ______________
Ð
MAT = _____________ Ð
AMH = ______________
Move the points around on the circle, paying attention to the measure of the angles for different shapes of the quadrilateral.
Find an interesting conjecture about the angles of a quadrilateral which has its vertices on a circle. Write it here.
Conjecture:________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
Close and do not save this sketch.
Exercise 5: A Triangle
1. Place three noncollinear points on the sketch. Label them A, B and C.
2. Select all three of your points. Go to the CONSTRUCT Menu, and select SEGMENT.
You should now have a triangle on your sketch.
3. Select the pointer (little arrow), and highlight side sBC of your triangle.
Go to the CONSTRUCT Menu, and select POINT ON OBJECT.
4. Label this new point E. Construct segment sAE.
Your sketch should look like this:
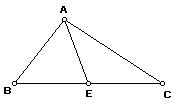
5. Highlight point B and point E. Measure the length of BE. BE = ___________
6. Highlight point C and point E. Measure the length of CE. CE = ___________
7. Measure Ð
BAE and Ð
CAE. Ð
BAE = ____________ and Ð
CAE = _________.
8. Measure AB and AC. AB = _____________ AC = ________________.
9. Move points around so that Ð
BAE = Ð
CAE and AB = AC.
What are the measures of BE and EC? BE = ______ EC = ____________
10. Move points around so that Ð
BAE = Ð
CAE and AB < AC.
What are the measures of BE and EC? BE = ______ EC = ____________
11. Move points around so that BE = EC and AB = AC.
What are the measures of Ð
CAE and Ð
BAE? Ð
CAE = ______ Ð
BAE = _________
12. Move points around so that BE = EC and AB < AC.
What are the measures of Ð
CAE and Ð
BAE? Ð
CAE = ______ Ð
BAE = _________
On the back of this page, write interesting conjectures about the angles and segments you have investigated.

