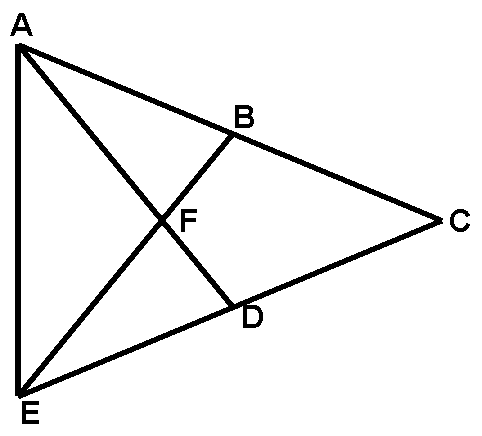
Geometry / Mr. Hansen
Sample Problem for Test #3 (Oct. 2000)

Name: __________________________

Given:

Ð BAD @ Ð FED
Ð AEC @ Ð EAC
AB = DE

Prove:

D BFD is isosceles

The following proof was given by a student in class but contains a small error. Can you find the mistake? (Answer is at bottom of page. Don’t peek until you have thought about the problem seriously. You can really learn something from this proof!)

INCORRECT PROOF
1. Ð BAD @ Ð FED
2. Ð AEC @ Ð EAC
3. AB = DE
4. sAB @ sDE
5. Ð AFB @ Ð EFD
6. D ABF @ D EDF
7. sBF @ sDF
8. D BFD is isosceles


1. Given.
2. Given.
3. Given.
4. Def. of @ segments
5. Vertical Ð s
6. ASA (1, 4, 5)
7. CPCTC
8. Def. of isosceles D

CORRECT PROOF
1. Ð BAD @ Ð FED
2. Ð AEC @ Ð EAC
3. AB = DE
4. sAB @ sDE
5. Ð FAE @ Ð AEF
6. sAF @ sEF
7. D ABF @ D EDF
8. sBF @ sDF
9. D BFD is isosceles


1. Given.
2. Given.
3. Given.
4. Def. of @ segments
5. Subtraction prop. for Ð s (steps 1, 2)
6. Base Ð s of D are @ iff opp. sides are @
7. SAS (steps 4, 1, 6)
8. CPCTC
9. Def. of isosceles D

Explanation of why the first proof is slightly incorrect:
Don’t read below the line until you have searched earnestly for the error! There is much knowledge to be gained by searching for the error!


Hint: The problem is in step 6. Can you find the problem?

If you are still stuck, try this hint: Verify that the ASA postulate is indeed satisfied in step 6. Now can you get it?

Answer (for those who have thrown in the towel): ASA is not satisfied in step 6, since ASA requires two angles and the side between them to be congruent. What we actually have here is a case of AAS. Now, as it turns out, AAS is a legitimate theorem, but we haven’t really proved it yet (see pp. 302-303 in textbook).

If the justification had been stated as AAS instead of ASA, we would have to accept the first proof as correct. However, the second proof is preferable because it uses only what the textbook has formally presented up to this point.