1.(a)

94°, since opp. Ðs of an inscr. quad. are supp.

(b)

Let A be the vertex at the left of the diagram. Call the points of tangency S and T, and let C be the center of the circle. Then ÐASC and ÐATC are rt. Ðs, so 180° of the angles in quadrilateral ASCT are already accounted for. Therefore, ÐSAT and ÐSCT are supp. (since all four Ðs in quad. ASCT must add up to 360°). But mÐSCT = 86 (central angle for arc SCT), so mÐSAT = 94.

Answer: 94°.

There is also a theorem that lets you conclude this directly, but you probably already have enough theorems rattling around in your brain.

(c)

43°, since whenever an angle’s vertex lies on the rim of a circle, the angle is ½ the intercepted arc. (See p.472.)

2.

Let W denote the intersection of sAD and sBC, and let Z denote the intersection of line AC and line BD. We know mÐCAD = 17 (half of intercepted arc CD), and mÐACW = 49 (half of intercepted arc AB). Therefore, since x is an exterior Ð for DAWC, x = 17° + 49° = 66°.

The second part of the problem (finding y) is much easier: y is simply half the difference between the intercepted arcs (see p.472), or ½(98° – 34°) = 32°.

3.(a)

Since 6 · 8 = 4 · BE, BE must equal 12. Therefore, BD = BE + ED = 12 + 4 = 16.

(b)

Since (PT)² = 4(4 + 12) = 64, PT = 8. See Power Thms. on pp.493-494.

(c)

Let a = XW. By Power Thm., 5(5 + a) = 3(3 + 12), so 25 + 5a = 45. Solving, we get a = 4.

4.(a)

The chord is being bisected (by Thm. 74, p.441), so we have a 5-12-13 rt. D. Radius = 13.

(b)

The Ð that looks like a rt. Ð actually is one, since an Ð inscr. in a semicircle is always a rt. Ð. Therefore, we have an 8-15-17 rt. D. Radius = 17/2 = 8.5.

(c)

If we connected the point of tangency shown to the center, the Ð so formed would be a rt. Ð. Therefore, we would have a 7-24-25 rt. D. Radius = 7.

5.

Half the intercepted arc on the large circle gives mÐWPX = 55. After that, the problem is virtually identical to problem #1(b) above. Answer: 125.

6.

Since arc BC = 160° (given), arc CDA must be the same (since BC = AC). We now have 320° accounted for in the circle, leaving 40° for arc AB.

Since Ð DAC = 70° (given), arc CD = 140°. Earlier we learned that arc CDA = 160°, so arc AD must be the remaining 20°.

7.(a)

The entire circle has circumference 2pr = 2p(6) = 12p. Therefore, the sector shown accounts for 45/360 of that length. Answer: (45/360) · 12p = 3p/2.

(b)

Add two radii to answer from part (a). Answer: 3p/2 + 12.

16.(a)

Let m = CX and let n = XB. Using the "walk-around" technique, we get the following diagram:

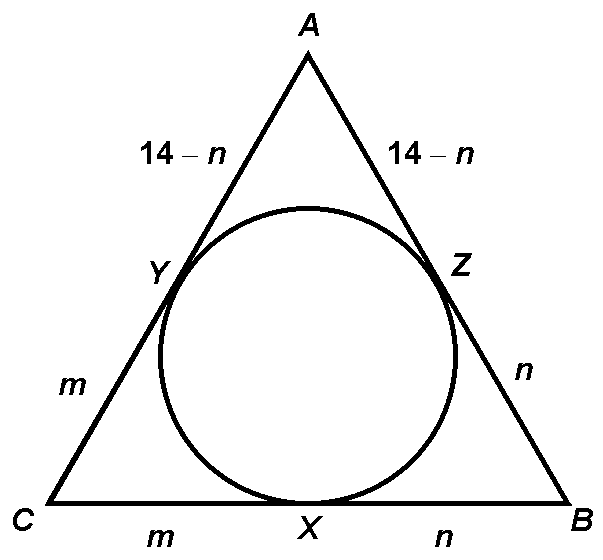
We can write an equation for the perimeter: 2m + 2n + (28 – 2n) = 38. Solve to get m = 5, which is the answer to part (a).

(b)

Our diagram can now be marked up as shown below, where BX = n is the unknown quantity of interest:

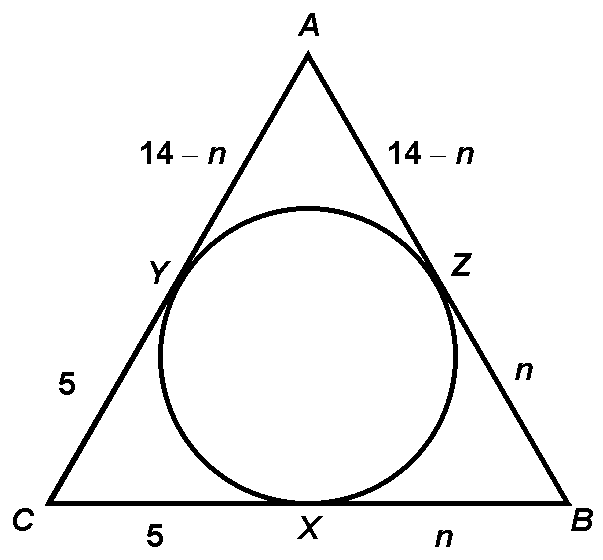
Examine side CB. What are the possibilities?

Case 1: AB = 14, and the other two legs are equal. They must each be 12 in order to satisfy the perimeter. Thus BC = 12, and BX = 7 by diagram.

Case 2: AB and AC are both 14, and sBC is the unequal leg. Clearly, BC = 10 in order to satisfy the perimeter, and BX = 5 by diagram.

Case 3: AB and BC are both 14, and sAC is the unequal leg (specifically, AC = 10). Then BX = 9 by diagram.

Answer: The possibilities for BX are 5, 7, or 9.

17.

Treat the arcs as being x, 2x, 5x, and 4x. If you draw a diagram, you can see that the inscribed angles must be half of (2x + 5x), half of (5x + 4x), half of (4x + x), and half of (x + 2x). Not only that, but half of (2x + 5x) must be supp. to half of (4x + x), and half of (x + 2x) must be supp. to half of (5x + 4x).

Writing equations, we get ½(2x + 5x) + ½(4x + x) = 180, or we could use ½(x + 2x) + ½(5x + 4x) = 180. Either way, x = 30°, so the angles are as follows:

½(2x + 5x) = 105°
½(5x + 4x) = 135°
½(4x + x) = 75°
½(x + 2x) = 45°

18.

The book’s diagram is terrible! This is an example of why you can never assume that a diagram shows angles in their proper proportions. If the figure were drawn correctly, sZY would have to be well above the center of the circle.

At any rate, note that m(arc AD) = 240 by process of elimination. Now we can use facts from p.472 to solve for all the angles.

(a)

ÐX = ½(arc CAB – arc CB) = ½(320° – 40°) = 140°
Note: You could also use the supp. Ð fact as in problems #1(b) and #5 above.

(b)

ÐY = ½(arc DCB – arc AB) = ½(90° – 30°) = 30°

(c)

ÐZ = ½(arc CBA – arc CD) = ½(70° – 50°) = 10°
Note: As a quick check on your work, make sure ÐX + ÐY + ÐZ = 180°.

19.

Extend sQO to the far side of the circle and call the resulting diameter sDQ. By Power Thm., (TP)² = PQ · PD, so 225 = 5 · PD. Therefore, PD = 45, so QD = 40. Radius = 20.

20.

Let x = m(arc AB), y = m(arc CD). We have a system of equations:

30 = ½(x – y)
x + y + m(arc AD) + m(arc BC) = 360

Since we were given m(arc AD) + m(arc BC) = 200, we can substitute into the second eqn. and write the much simpler form x + y + 200 = 360.

After simplifying further and solving the system for x and y, we get x = m(arc AB) = 110, y = m(arc CD) = 50.

23.

By Power Thm., 10² = 5(5 + x + 9). Solve to get x = 6.

Then use Chord-Chord Power Thm. to say 9x = 3y. Since x = 6 from above, y = 18.