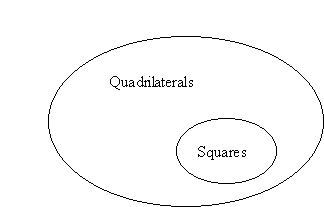
If a figure is a square, then it is a quadrilateral.
Conditional Statements
rev. 9/15/2000
If (hypothesis) then (conclusion).
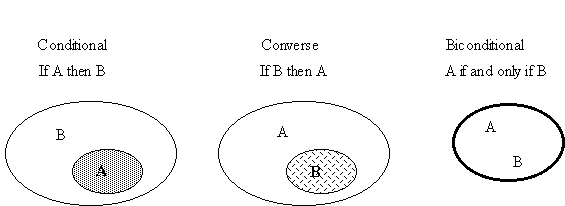
If A, then B.
This statement means that the set of all things which are A is a subset of all things which are B. It does not tell you anything about things which are not A, nor does it tell you much about things which are B.
Consider this true conditional statement:
If a figure is a square, then it is a quadrilateral.

Here are different grammatical forms of the same conditional statement:
If it is a square, then it is a quadrilateral. If A, then B.
square Þ quadrilateral. A Þ B
It is a quadrilateral if it is a square. B if A
It is a square only if it is a quadrilateral. A only if B
There are ways to rearrange the component parts of a conditional statement to create different, related statements.
Basic Conditional Statement: If A, then B. A Þ B
Converse: If B, then A. B Þ A
Inverse: If A is not true, then B is not true. ~A Þ ~B
Contrapositive: If B is not true, then A is not true. ~B Þ ~A
Example:
Original Statement: If a figure is a square, then it is a quadrilateral.
Converse: If a figure is a quadrilateral, then it is a square.
Inverse: If a figure is not a square, then it is not a quadrilateral.
Contrapositive: If a figure is not a quadrilateral, then it is not a square.
A biconditional statement ( A Û B) is a conditional statement for which both the statement and the converse are true. A definition must be a biconditional statement.
Another name for a biconditional statement is an "iff" (if and only if) statement.