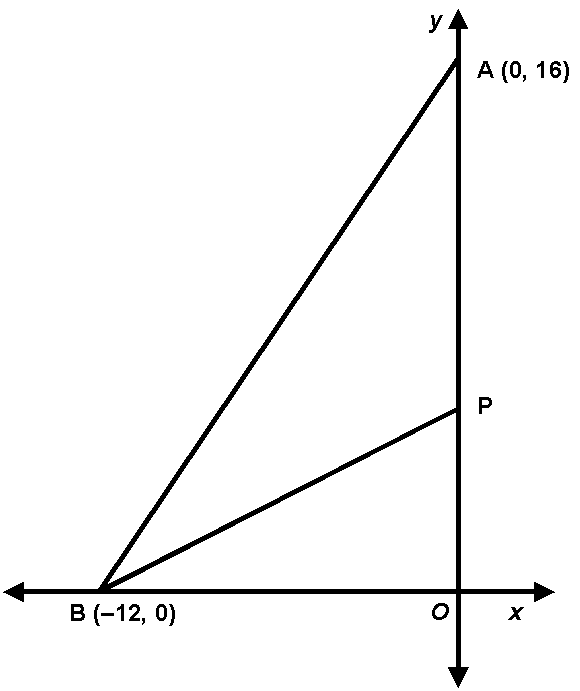Practice Midterm Exam

Geometry / Mr. Kelley, Mr. Graham, Mr. Hansen
Posted 12/26/2000 [rev. 1/12/2003, 12/13/2008]

Name: _______________________

Instructions and Study Guide:

This practice exam is designed to stimulate your brain during Christmas break. For additional practice, you should read the chapter summaries and should work a few review problems at the end of each chapter.
Although the actual exam will be shorter and somewhat easier, you should be able to solve all of these problems.
Work all problems, or if you prefer, you may do the odd-numbered (easier) ones first, then the even-numbered ones.
You need to show your work only if the problem says "prove" or "show." The majority of the problems, both here and on the actual exam, will be short answer, matching, or multiple choice.
The actual exam will have a few proofs. Be sure to practice some 2-column proofs from the review problems at the end of each chapter, including problems in which the diagram is not provided.
The answer key will be posted at a later date.
Formulas will not be listed on the actual exam. For your convenience in studying, here are all the formulas you are expected to know by heart:

Pythagorean Theorem: c² = a² + b²
Area of a circle: A = pr²
Circumference of a circle: C = 2pr = pd
Value of pi: p » 3.14159
Area of a triangle: A = ½ bh
Area of a rectangle: A = wh
Perimeter of a rectangle: P = 2w + 2h
Perimeter of other figures: [use common sense to add up the lengths of the sides]
Volume of a rectangular box: V = lwh
Logical statements: If P Þ Q is the basic statement of interest, then Q Þ P is the converse, ~P Þ ~Q is the inverse, and ~Q Þ ~P is the contrapositive. Any statement and its contrapositive are always equivalent (i.e., they have the same truth value—either both true or both false). Also, the converse and the inverse are always equivalent. However, a statement and its converse (or a statement and its inverse) need not have the same truth value.
What a definition is: Saying that statement A is defined by statement B means that A and B are equivalent, i.e., they have the same truth value, i.e., A Þ B and B Þ A. The shorthand for this is A Û B, sometimes written "A iff B" and pronounced "A if and only if B."
[Example: A rhombus is defined to be a quadrilateral with all 4 sides congruent. Another way of expressing this would be to say, "A quadrilateral is a rhombus if and only if all 4 sides are congruent."]
Arithmetic mean of x and y: arith. mean = (x + y)/2
[This is simply the "average" of two numbers.]
Geometric mean of x and y: geo. mean = , provided xy > 0
[These are the solutions for a in the proportion x:a = a:y that you get by cross-multiplying. That’s right, there are 2 solutions. However, in geometry class, we always take the positive solution because we are interested in the geometric mean as a length of a segment. Next year, in Algebra II, you will be required to find both solutions.]
Midpoint of segment from point (a, b) to point (c, d): x coordinate = (a + c)/2, y coordinate = (b + d)/2
[In other words, the midpoint M is the point ((a + c)/2, (b + d)/2). Basically, you are just averaging the x coordinates and the y coordinates. The formula is also useful in problems where you are told what the midpoint is and have to figure out one of the endpoints. See #55 below for a problem of this type.]
Slope of segment from point (a, b) to point (c, d): m = rise/run
[Other ways to express this: m = Dy/Dx = (change in y) / (change in x) = (d – b) / (c – a).
You can also get the correct answer with m = (b – d) / (a – c). Just be sure to subtract carefully.]
Slope of a horizontal line: m = 0
Slope of a vertical line: m = undefined (DNE)
Slopes of perpendicular lines: m₁m₂ = –1; i.e., m₂ = –1/m₁ ("negative reciprocal")
[Note: This formula does not apply if one line is horizontal and the other is vertical.]
Sum of interior angle measures (convex n-gon): (n – 2) · 180
[Examples: triangle = 180, convex quadrilateral = 360, convex pentagon = 540, convex hexagon = 720.]
Single interior angle measure (regular n-gon): (n – 2) · 180/n
Sum of exterior angle measures (convex n-gon): 360
Single exterior angle measure (regular n-gon): 360/n

Memorize all the definitions of the special quadrilaterals we studied. Other properties should be familiar to you but do not necessarily have to be memorized. Here are all of them, for your convenience in studying:

General Convex Quadrilateral
Definition: 4-sided plane figure in which each _______ angle has a measure of less than _______
Other properties:
any segment connecting 2 interior points must lie wholly within the interior
sum of interior angle measures = _______
figure formed by connecting midpoints of sides is a _______

Trapezoid
Definition: quadrilateral with 2 sides ("bases") parallel, 2 sides ("legs") not parallel

Isosceles Trapezoid
Definition: trapezoid in which the legs are _______
Other properties:
diagonals are congruent
upper base angles are congruent
lower base angles are congruent
any lower base angle is _______ to any upper base angle

Kite
Definition: quadrilateral with consecutive sides having lengths a, a, b, b
(if a = b we have a special kind of kite, namely a _____________)
If the kite definition is satisfied by a nonconvex quadrilateral, we have a figure known as a dart. All darts are kites, but not all kites are darts.
Other properties:
at least one diagonal is the ^ _______ of the other
at least one diagonal _______ the angles at each end
at least one pair of congruent opposite _______
A kite can be thought of as 2 congruent mirror-image triangles glued together along a common side.

Parallelogram
Definition: quadrilateral in which both pairs of opposite sides are _______
(suffices to show both pairs congruent, or one pair parallel and congruent)
Other properties:
any 2 opposite sides are _______
any 2 opposite angles are _______
any 2 consecutive angles are _______
diagonals _______ each other
But note: diagonals do not necessarily bisect their angles. (If one diagonal bisects its angles, we have a kite. If both diagonals bisect their angles, we have a rhombus.)
A parallelogram can be thought of as 2 congruent triangles (one of them rotated 180° ) glued together along a common side.

Rhombus
Definition: an equilateral quadrilateral (i.e., all 4 sides _______)
Other properties:
all properties of kites and parallelograms (since a _______ is both a kite and a parallelogram)
_______ are ^ bisectors of each other
diagonals _______ their angles
A rhombus can be thought of as 4 congruent right triangles glued together back-to-back and bottom-to-top (these are the 4 triangles created by drawing the diagonals of the rhombus).

Rectangle
Definition: parallelogram with a _______ angle
Other properties:
all properties of parallelograms
all 4 angles are right angles
diagonals are _______

Square
Definition: an equilateral rectangle (i.e., a rectangle that is also a rhombus, or you could say a rectangle that is also a _______)
Other properties:
all properties of rhombuses and rectangles (since a square is both a rhombus and a rectangle)
_______ divide the square into 4 isosceles right triangles (45°-45°-90° triangles)

Here is the Practice Exam
Please read the instructions/study guide above before beginning. Please work all problems. If time is limited, work the odd-numbered problems first, since they are easier, and work a selection of even-numbered problems for additional challenge.

	*In problems 1-20, write A, S, or N depending on whether the statement is always* true, sometimes true, or never true.**
1.	Equilateral triangles are similar.
2.	If a theorem is true, then its converse is also true.
3.	The complement of an acute angle is obtuse.
4.	If the segments joining the midpoints of the opposite sides of a quadrilateral are perpendicular to the sides, then the quadrilateral is a rectangle.
5.	Two lines perpendicular to the same plane are parallel to each other.
6.	The sum of two sides of a triangle is half its perimeter.
7.	If two coplanar isosceles triangles share the same base, the line joining their vertices will be the perpendicular bisector of the base.
8.	If two coplanar lines are cut by a transversal so that alternate interior angles are complementary, then the given lines intersect to form an angle whose measure equals the difference between the measures of the complementary angles.
9.	The diagonals of a trapezoid bisect each other.
10.	If two lines are skew, then there exists a line that is parallel to both of the lines.
11.	The diagonals of a kite are perpendicular bisectors of each other.
12.	If two points are each equidistant from the endpoints of a segment, then the endpoints of the segment are equidistant from the two points.
13.	As the number of sides of a convex polygon increases, the sum of the measures of its interior angles increases in increments of 180.
14.	If a ray bisects an exterior angle of a triangle, then the ray is parallel to the opposite side of the triangle.
15.	The sum of the measures of two exterior angles (at different vertices) of a triangle is greater than 180.
16.	If each leg of a right triangle is a multiple of n, then the hypotenuse is also a multiple of n.
17.	An obtuse triangle is congruent to an isosceles triangle.
18.	An obtuse triangle is similar to an acute triangle.
19.	Each exterior angle of a regular octagon has a measure greater than each exterior angle of a regular heptagon (i.e., 7-gon).
20.	If a pair of opposite angles of a convex quadrilateral are complementary, then the exterior angles for the remaining pair of angles are also complementary.
21.	If two angles of one triangle are congruent to two angles of another triangle, then the remaining corresponding angles are . . . (A) congruent (B) supplementary (C) complementary (D) acute (E) obtuse
22.	How much larger is the arithmetic mean of 18 and 50 than the geometric mean of those numbers? (A) 4 (B) 32 (C) 38 (D) more than 100 (E) The arithmetic mean and geometric mean are equal.
23.	The sum of the angle measures in a convex pentadecagon (15-gon) is _______ .
24.	If consecutive angles of a quadrilateral have measures in the ratio 3:4:5:6, then it must be the case that the quadrilateral . . . (A) can be inscribed in a circle (B) is a kite (C) is a trapezoid (D) has congruent diagonals (E) is not convex
25.	Find P', the point that results when point P(–6, 7) is rotated 180° clockwise about the origin.
26.	Given straight angle APF, ray PB and ray PC trisecting obtuse ÐAPD, ray PE bisecting acute ÐDPF, and mÐCPE = 69, show your work and compute mÐAPE.
27.	One of the trisectors of a right angle divides it into two angles. The ratio of the smaller angle to the larger angle is . . . (A) 1:2 (B) 1:3 (C) 2:3 (D) 1:1 (E) none of the above
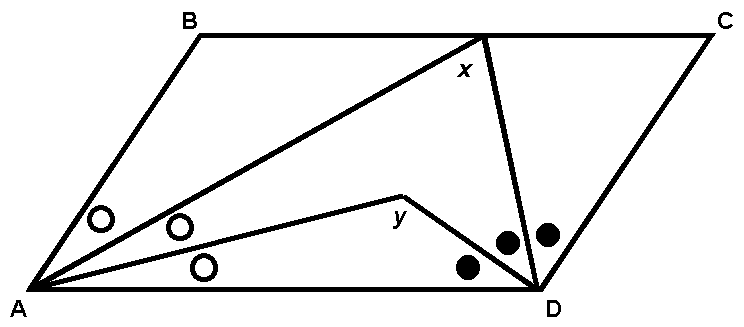
28.	Quadrilateral ABCD is a parallelogram, and the angles at A and D have been trisected. Find the sum of the measures of x and y. (A) 90 (B) 120 (C) 180 (D) 140 (E) insufficient information
29.	Which of the following are equilateral quadrilaterals? (A) parallelogram and rectangle (B) kite and rhombus (C) square and rhombus (D) none of the above
30.	The slope of a line is –5/2. The line contains (5, 11) and a point whose x coordinate is 10. Compute the point’s y coordinate.
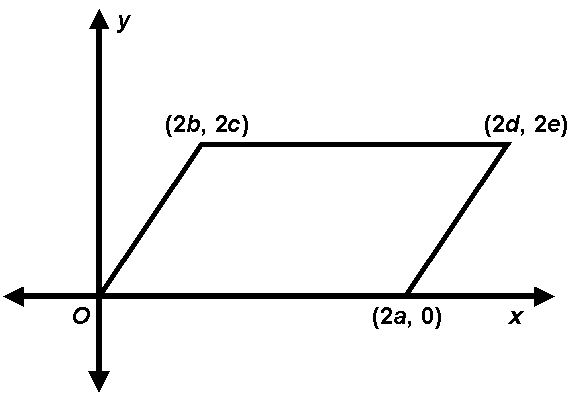
31.	If the figure above shows a parallelogram, why does (d, e) = (a + b, c)? (A) Opposite sides of parallelogram are \|\|. (B) Opposite sides of parallelogram are @. (C) Opposite angles of a parallelogram are @. (D) Diagonals of a parallelogram bisect each other. (E) If the midpoints of consecutive sides of a parallelogram are joined, another parallelogram is formed.
32.	If 2 angles are such that their supplements are complementary, then compute the sum of the measures of the original 2 angles.
33.	If ÐP and ÐQ are supplementary and congruent, which of the following must be true? (A) ÐP and ÐQ are right angles (B) ÐP and ÐQ are straight angles (C) ÐP and ÐQ are each 45° (D) ÐP and ÐQ are vertical angles (E) none of the above
34.	If P is on line j, Q is on line k, and segment PQ is ^ to both j and k, then . . . (A) j \|\| k (B) j ^ k (C) j and k are skew (D) Any of the above may be true. (E) Either (A) or (C) is true.
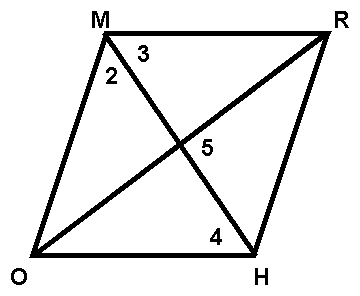
35.	In the diagram above, quadrilateral RHOM is a rhombus. Which of the following is not necessarily true? (A) Ð5 = 90° (B) Ð2 @ Ð3 (C) Ð2 @ Ð4 (D) mÐ5 > mÐ4 (E) none of the above (i.e., statements (A) through (D) must all be true)
36.	Given trapezoid ABCD with segment AB \|\| segment CD, we can conclude that . . . (A) ÐA comp. ÐD (B) ÐA supp. ÐD (C) ÐA @ ÐD (D) segment AC @ segment BD (E) segment AC and segment BD bisect each other
37.	An angle is ¼ as large as its supplement. Find the measure of the complement of the angle. (A) 36 (B) 54 (C) 72 (D) 144 (E) none of the above
38.	Find the distance between the trisection points of the segment joining (–7, 10) and (5, –6).
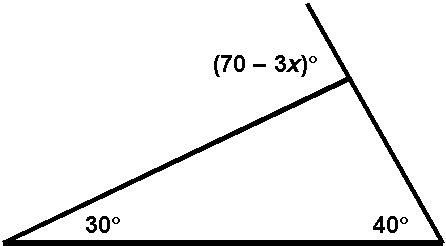
39.	Solve for x. (A) 46 2/3 (B) 1/3 (C) 0 (D) Æ (E) insufficient information
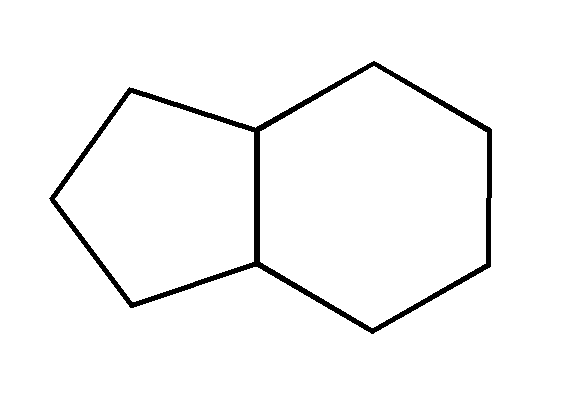
40.	Given two regular polygons joined as shown with a congruent side in common, what is the regular polygon with the largest number of sides that will fit without overlap into the "V" at the top of the diagram? (A) square (B) pentagon (C) hexagon (D) heptagon (E) octagon
41.	Find the measure of each interior angle of a regular octagon. (A) 45 (B) 60 (C) 120 (D) 135 (E) insufficient information
42.	If ÐA supp. ÐB, ÐB comp. ÐC, and the ratio of mÐA to mÐC is 7:2, compute mÐB.
43.	Two sides of a triangle have lengths 6 and 8. Which of the following could not be the length of the third side? (A) 2 (B) 5 (C) 8 (D) 10 (E) 13
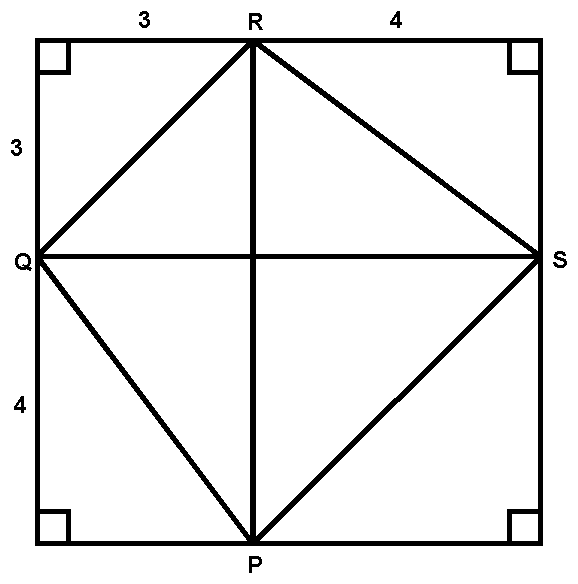
44.	The diagram has the origin at its lower left corner, point P on the x-axis, and point Q on the y-axis. Segments RP and QS are vertical and horizontal, respectively. Prove that quadrilateral PQRS is a trapezoid and compute its perimeter (show work).
45.	Given: E is the intersection of segment AC and segment BD, and DDCE @ DBAE. Which of the following is not necessarily true? (A) line AD is parallel to line BC (B) line CD is parallel to line AB (C) line AC bisects segment BD (D) E is the midpoint of segment AC (E) none of the above (i.e., statements (A) through (D) must all be true)
46.	The sum of the exterior angles of a regular polygon is 360. What is the name of the polygon? (A) triangle (B) square (C) pentagon (D) hexagon (E) insufficient information
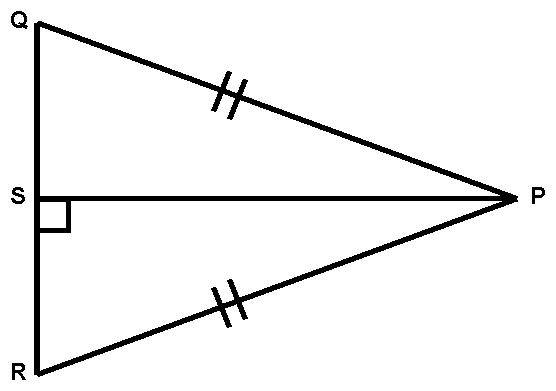
47.	DPSQ @ DPSR by . . . (A) SAS (B) SSS (C) SSA (D) HL (E) The triangles are not necessarily @.
48.	Given points P(0, 3), Q(12, 8), and R(15, 3), estimate ÐPQR. (A) 5.1° (B) 22.6° (C) 42.7° (D) 67.4° (E) 83.2°
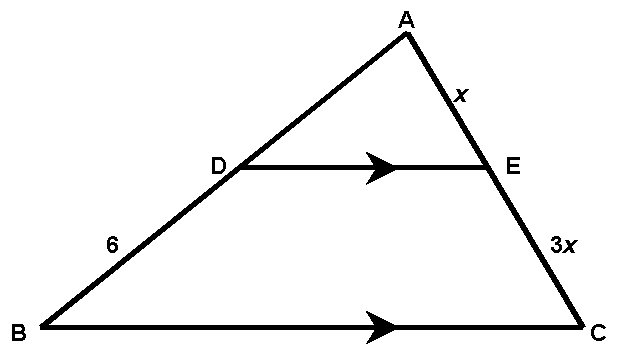
49.	AB equals . . . (A) 2 (B) 2x (C) 8 (D) 8x (E) insufficient information
50.	If DCAT @ DDOG, CT = 5x – 3, DO = 25 + x, AT = 3x, DG = y, and CA = y + 6, show work and compute GO.
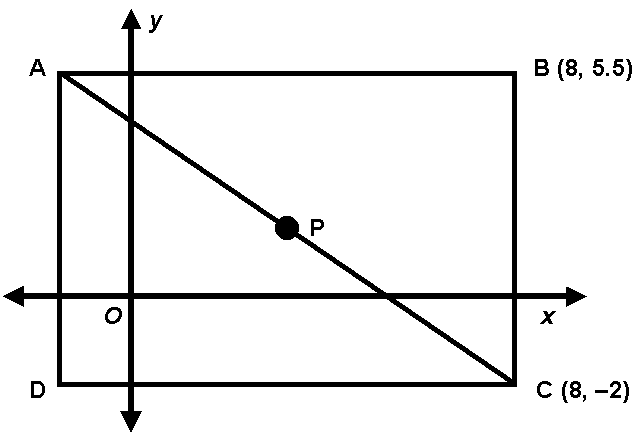
51.	If ABCD is a rectangle and the x coordinate of D is –1.5, calculate the coordinates of P, the midpoint of segment AC.
52.	In a triangle with sides of length 5, 8, and 2x + 9, find the restrictions on the value of x. (A) –2 < x < 4.5 (B) –3 < x < 2 (C) 0 < x < 2 (D) –4.5 < x < 7 (E) –13 < x < 14
53.	In right triangle ABC, where ÐC is the right angle, BC > AC. Find the restrictions on mÐA. (A) 0 < mÐA < 45 (B) 0 < mÐA < 60 (C) 0 < mÐA < 90 (D) 30 < mÐA < 60 (E) 45 < mÐA < 90
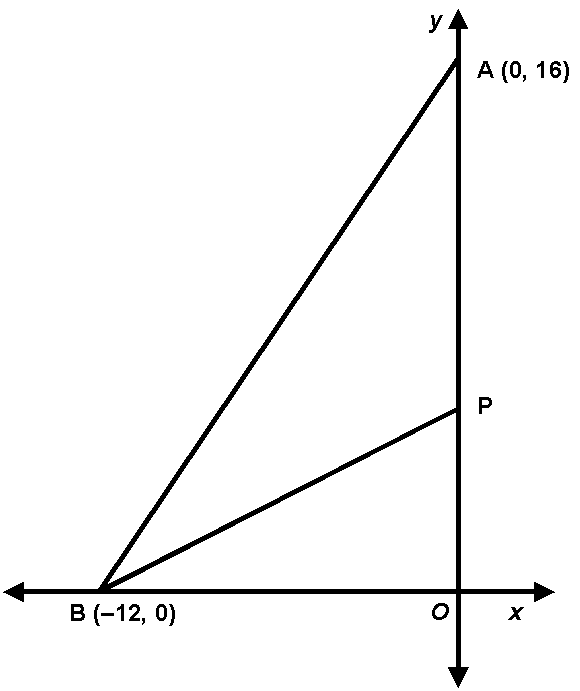
54.	Given: diagram as shown, where ray BP bisects ÐABO, OA = 16, and OB = 12 Prove: P is the point (0, 6)
55.	Given that Z (11, –11) is the midpoint of segment QR, where Q has coordinates (5, p) and R has coordinates (s, t), which of the following is true? (A) s = 17 and t = p + 22 (B) s = 17 and t = –p + 22 (C) s = 17 and t = –(p + 22) (D) s = 17 and t = p – 22 (E) none of the above
56.	In the diagram in #54, add point M midway between A and B, and assume that the conclusion of #54 has already been proved. Also assume that you have already computed AB, which is 20. Given: diagram as above, with M the midpoint of segment AB, OP = 6, and AB = 20 Prove: mÐBPM = 45
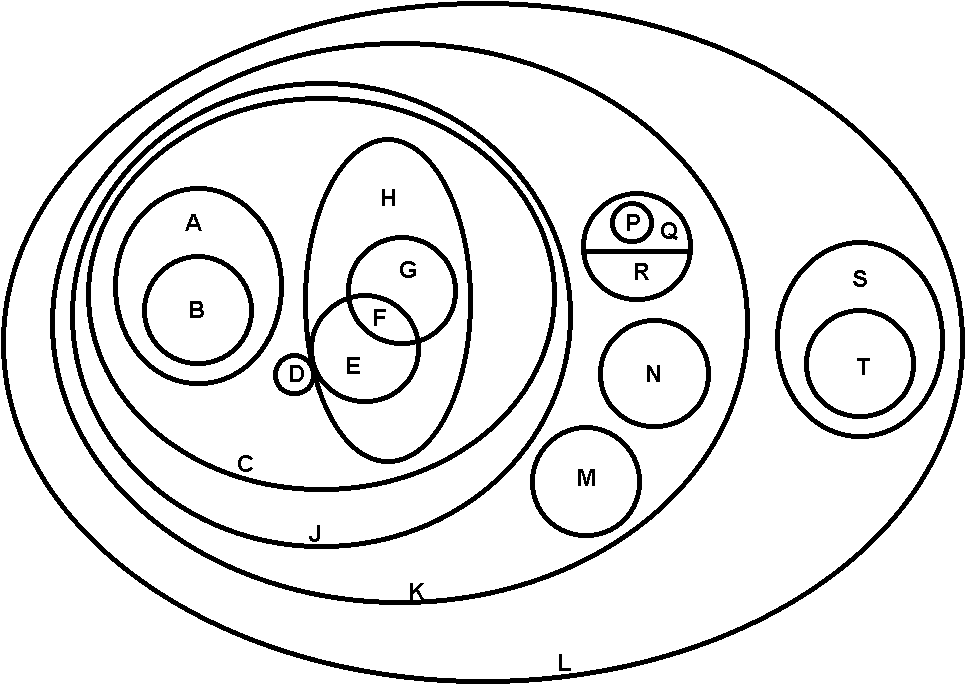
57.	Match each of the labeled regions in the Venn diagram to the correct name below. ___ hexagons ___ rhombuses ___ plane figures ___ squares ___ pentagons ___ ellipses ___ quadrilaterals ___ polygons ___ isosceles triangles ___ rectangles ___ parallelograms ___ equilateral triangles ___ circles ___ trapezoids ___ isosceles trapezoids ___ convex quadrilaterals ___ scalene triangles ___ convex kites that are not rhombuses
58.	Refer to the diagram above. If D = {convex kites that are not rhombuses} and E = {rhombuses}, what name is given to D È E? (A) {rhombuses} (B) {convex kites} (C) {rhombuses that are not convex kites} (D) {convex kites that are not rhombuses} (E) { }
59.	Refer to the diagram above. If Q = {isosceles triangles} and R = {scalene triangles}, then what name is given to Q È R? (A) {triangles} (B) {equilateral triangles} (C) {isosceles triangles} (D) {circles} (E) { }
60.	Which of the following would be a correct way of denoting the empty set? Mark all that apply. (A) Æ (B) {Æ} (C) { } (D) 0 (E) none of the above
61.	Which of the following is the contrapositive of "When Woody is hungry, he eats everything in sight"? (A) If Woody is not hungry, he does not eat everything in sight. (B) If Woody is not eating everything in sight, he is not hungry. (C) If Woody is eating everything in sight, he is hungry. (D) If Woody is hungry, he is not necessarily eating everything in sight. (E) none of the above
62.	Find a statement that is equivalent to the converse of the following statement: "Every American who is convicted of a serious crime will serve time in prison." (A) If you serve time in prison, then you are an American who did not commit a serious crime. (B) If you serve time in prison, then you are either an American or a person who committed a serious crime (or both). (C) If you serve time in prison, then you are neither an American nor a person who committed a serious crime. (D) If you serve time in prison, then you are both an American and a person who committed a serious crime. (E) none of the above
	*For problems 63 through 68, write the name of the quadrilateral that most precisely describes plane figure ABCD.*

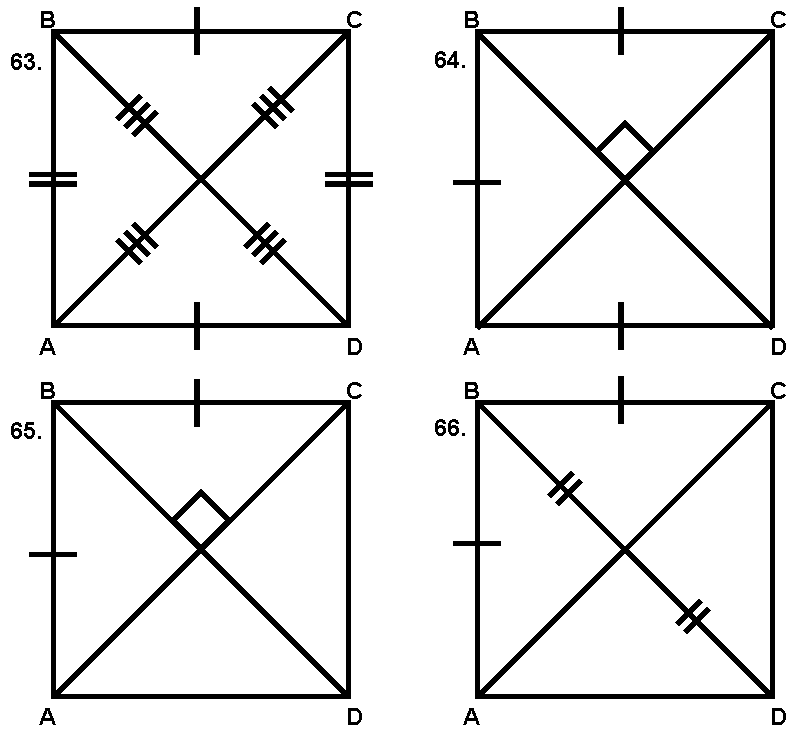
67.	If the diagonals in #66 are perpendicular, ABCD must be a _______ .
68.	If the diagonals in #66 are perpendicular and BD = AC, then ABCD must be a _______ .
69.	As you may know, the Washington Monument is 555 feet tall. At a moment when the monument is casting a 215-foot shadow, a visiting celebrity is observed to be casting a shadow exactly 2 feet, 9¾ inches long. How tall is the celebrity, and what league does he or she play in? Show a diagram and your work.
70.	As has been known for millennia, the full moon occupies almost exactly the same apparent portion of the sky that the sun does. This remarkable coincidence is most noticeable during a solar eclipse, when only the faintest rim of the sun (its corona) is visible. If the moon has a diameter of about 3500 km and a mean distance from the earth of approximately 380,000 km, and if the sun's mean distance from earth is approximately 150 million km (93 million miles), compute the sun's diameter to the nearest 10,000 miles. Show a diagram and your work.