[Editorial note from Mr. Hansen:
I wish to thank the committee of authors: Messrs. Cho, Gandal, Paley, and Swartz. This practice test gives a good indication of the level of difficulty to expect on the actual test, although the mix of problems may be somewhat different and, of course, the numbers and verbal settings of the problems will be different. For example, some of the concepts treated in the multiple choice section may be treated in greater depth as a free response question, or some portions of the actual test may be designed to require use of a graphing calculator. Also, because the practice test does not cover generalized max/min problems, it would be prudent to expect a problem comparable in difficulty to those on pp.530-532 of the textbook. At the difficulty level represented below, you should be able to work all 13 problems in 50 minutes. In the actual test, the multiple choice questions will probably be either a bit easier or slightly less numerous (e.g., choose 8 or 9 out of 10). The free-response questions will probably be a bit harder.]
The following test has free response and multiple-choice questions. NO CALCULATOR is allowed. In the free-response section, all work is necessary for full credit.
- 1.
|
The velocity of Peters 1971 Ferrari 250 GT California, v(t), is given by the function v(t) = 2t 3, where t is in seconds and v(t) is in meters per second. |
|
(a) |
Find the distance that the car travels from t = 0 to t = 2. |
|
|
|
|
|
|
|
(b) |
At the end of this time interval, where is Peter located relative to his starting position? Has his net travel been forward or backward? |
|
|
|
|
|
|
|
(c) |
What is Peters average velocity on this time interval? His average speed? |
|
|
|
|
|
|
- 2.
|
Yoon is standing on the sidewalk of a street and sees an attractive young lady on the sidewalk on the other side of the street. Yoon wants to go meet the girl. He can walk at 2 meters/second while on the sidewalk; however, when he crosses the street Yoon can walk at a rate of Ö2 meters/second. The width of the road is 12 meters. The horizontal distance between Yoon and the girl is 20 meters. (Assume both stand on the very edge of the sidewalk closest to the road).
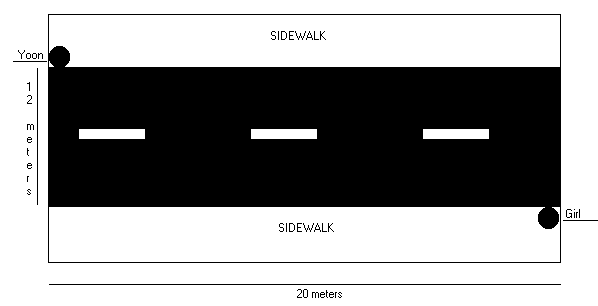 |
|
(a) |
What is the minimum amount of time it would take for Yoon to reach the girl? |
|
|
|
|
|
|
|
|
|
|
|
|
|
(b) |
Using the time allotted from part (a), how far does Yoon walk on the sidewalk? |
|
|
|
|
|
|
- 3.
|
The curvature of any parametric plane curve is given by the following formula:
curvature = df/ds = (x΄y΄΄ x΄΄y΄)/(|v|3)
Here, f denotes the angle that a line tangent to the curve makes with the x-axis, ds is the differential of arc length, the first and second derivatives shown are wrt parameter t, and |v| represents the magnitude of the velocity vector at time t.
Show that for a circle given by x = r cos t and y = r sin t, where r is a nonzero constant, curvature is a constant. |
Directions: A score of 4 points is given for each correct answer, 0 points for each answer omitted, and 1 point for a wrong answer. Do all of the following 10 problems.
|
1. |
If a(t) = 2t, find the distance traveled for 0 £ t £ 4, given that v(2) = 5. |
|
|
A) 44/3
B) 16
C) 21
D) 64/3
E) 64 |
|
2. |
Given position function r(t) = (10sin 3t/5) i + (4cos 3t/4) j, find v(5p). |
|
|
A) 1.5Ö2 i
B) 1.5Ö2 j
C) 3/2 i + Ö2 j
D) 6i + 1.5(Ö2) j
E) Ö2 i + 3/2 j |
|
3. |
The average value of cos x over the interval p/3 £ x £ p/2 is |
|
|
A) 3/p
B) ½
C) 3(2 Ö3)/p
D) 3/(2p)
E) 2/(3p) |
|
4. |
The average value of csc2 x over the interval from x = p/6 to x = p/4 is |
|
|
A) (3Ö3)/p
B) (Ö3)/p
C) 12/p · (Ö3 1)
D) 3Ö3
E) 3((Ö3) 1) |
|
5. |
The height of a rectangular box is 10 in. Its length increases at a rate of 2 in/sec; its width decreases at a rate of 4 in/sec. When the length is 8 in and the width is 6in, the volume of the box is changing, in cubic inches per second, at the rate of |
|
|
A) 200
B) 80
C) 80
D) 200
E) 20 |
|
6. |
A 26-foot ladder leans against a building so that its foot moves away from the building at a rate of 3 ft/sec. When the foot of the ladder is 10 ft from the building, the top is moving down at the rate of r ft/sec, where r is |
|
|
A) 46/3
B) Ύ
C) 5/4
D) 5/2
E) 4/5 |
|
7. |
The rate of change of the area of an equilateral triangle with respect to its side S at S = 2 is |
|
|
A) (Ö3)/4
B) Ö3
C) (Ö3)/2
D) 7
E) ½ |
|
8. |
A circular conical reservoir, vertex down, has depth 20 ft and radius of 10 ft. at the top. Water is leaking out so that the surface is falling at the rate of ½ ft per hour. The rate, in cubic feet per hour, at which the water is leaving the reservoir when the water is 8 feet deep is |
|
|
A) 4p
B) 8p
C) 16p
D) 1/(4p)
E) 1/(8p) |
|
9. |
Given position function r(t) = 144 sin(t/12) i + 144 cos(t/6) j, find the tangential component of a(3p). |
|
|
A) 3(Ö2)/5 i + (Ö2)/9 j
B) (Ö2)/18 i + 2/9 j
C) (Ö3)/18 i + (Ö2)/2 j
D) (Ö2)/18 i + 2/9 j
E) 3(Ö2)/5 i + 2/9 j |
|
10. |
Let x = x(t) be a dimensionless quantity that changes as a linear function of time t, where t is in seconds. If x(0) = x(1) + 2, and the position function of a particle is s(t) = x2 i + 3x3 j , find a(2). |
|
|
A) 8i + 72x j
B) 4i 36x j
C) 8i + 36j
D) 4i + 72j
E) 8i + 36x j |
