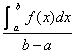BC Calculus Cram Sheet

[Courtesy of Will Felder. Revised 5/10/00, 1/25/01, 8/3/02, 5/8/03, 1/13/010, 12/20/010.]

Formulas	Trapezoid rule:
	Chain rule:
	Derivative of an inverse:
	Parametric chain rule: If y = y(t) and x = x(t), then .
	Product rule:
	Quotient rule:
	Change of base:
	Rewriting an exponential:
	Integration by parts:
	Polar area:
	Exponential growth: Diffeq. has solution y = Ce^kx if x is the independent vbl., or y = Ce^kt if time is the independent vbl.
	Logistic growth: Diffeq. has solution .
	Volume by disks: if axis of rotation is parallel to x-axis (use dy if parallel to y-axis)
	Volume by shells: if axis of rotation is parallel to y-axis (use dy if parallel to x-axis)
	Average value of f on [a, b] is .
	cos² x = (1 + cos 2x)
	sin² x = (1 – cos 2x)
	(Use first two terms on RHS for the so-called linear approximator.)
Derivatives and Antiderivatives
	Should know derivatives and antiderivatives of all of these function families:
	polynomials power functions (incl. negative and non-integer exponents) exponential logarithmic trigonometric (don’t forget ) inverse trigonometric (esp. arctan); arcsin and arccos are good to know Note: AP syllabus omits hyperbolic and inverse hyperbolic functions.
Arc Length	Regular:
	Parametric:
	Polar: (If needed, can also be derived from parametric using parameter , where x = r cos and y = r sin .)
IVT	If f is continuous on [a, b],
	then [or, wlog, if f (a) > f (b)]
	In words: For any intermediate value of a continuous function on a closed interval, there is at least one place in the interior of the open interval (a, b) where that intermediate value is actually attained. (Sometimes called the “Cape of Good Hope Theorem.”) Interesting corollary: If f and g are both continuous on [a, b] and their difference is negative at one endpoint and positive at the other, then there is at least one place in (a, b) where f (x) = g(x).
EVT	If f is continuous on [a, b],
	then f (x1) is the maximum value of f on [a, b] and f (x2) is the minimum value of f on [a, b].
	Alternate (more cryptic) version of the theorem: If f is continuous on [a, b], then .
	In words: A continuous function on a closed interval (the conditions are crucial) attains its maximum and minimum values somewhere on that closed interval.
MVT	If f is differentiable on (a, b) and continuous on [a, b],
	then .
	In words: There is at least one place where (slope of tangent line) equals (average slope between a and b). Conditions are crucial to know: f differentiable on (a, b) and continuous on [a, b].
FTC	If f is continuous (note: Riemann integrable is sufficient) on [a, b] and g is any antiderivative of f,
	then
	Equivalent form (sometimes called FTC2): If for a constant a and a continuous integrand f, then
Definitions	Derivative at a point:
	Derivative function:
Maclaurin and Taylor Series
	e^x = 1 + x + x^2/2! + x^3/3! + . . . [converges for all x]
	sin x = x – x^3/3! + x^5/5! – x^7/7! + x^9/9! – . . . [converges for all x]
	cos x = 1 – x^2/2! + x^4/4! – x^6/6! + x^8/8! – . . . [converges for all x]
	[converges if ]
	= 1 + x + x^2 + x^3 + x^4 + . . . [converges if |x| < 1 since geometric]
	Note: You need to know the intervals of convergence. The final “. . .” must be included in each case for full credit on the AP exam.
Taylor’s Theorem
	If f has derivatives of all order at a point c Df ,
	then where
	equals the following infinite series:
Notes on Taylor’s Theorem
	1. I is called the interval of convergence for the Taylor series.
	2. If the Taylor series is truncated after the first 2 terms, the result is the familiar linear approximator function. AP WARNING: In this case, you must write the symbol, not the = symbol, after the f (x). Here is an example of the correct format: .
	3. AP WARNING: If you write f (x) followed by an equal sign, write “. . .” at the end to show an infinite series. AP graders may deduct points if you omit the 3 dots.
AST Error Bound	|Rn| < |tn+1| In words: In a convergent alternating series with terms of decreasing absolute value, the magnitude of the error is bounded by the first omitted term.
Convergence Tests	See p.635 for summary of common tests, plus p.640 for integral test. Remember, the nth term test is a test for divergence: lim tn = 0 is a necessary but not sufficient condition for convergence.
Lagrange Bound	If M is the maximum absolute value of f ^(n + 1)(x) on the interval between a and x, then the nth-degree Taylor polynomial that approximates f (x) has a remainder (error) bounded as follows: .
Techniques for Multiple Choice		Techniques for Free Response
1. Pace yourself. Keep brainpower in reserve for free response. 2. Get the answer any way you can. Work is not graded for multiple choice. 3. Circle the hard ones and come back to them later. 4. If you can positively rule out one or more choices, choose randomly from those that remain. Do not make an educated guess, since you will probably fall into a trap. Note: Beginning in 2011, this advice is less important, because the guessing penalty has been eliminated. However, the general principle is still valid: Guess randomly from among the choices that you cannot rule out. 5. In an integral problem where a common mistake would be to be off by a factor of 2, look closely at the two choices that differ by a factor of 2. The correct answer is probably one of these.		1. If you can’t get part (a), skip it and do the others. Part (a) may be worth only a point. 2. A few lines of accurate work are usually enough. Long, tedious problems are rare. 3. Keep intermediate results in full precision (can use STO to save to a variable). Write “. . .” on paper if you are omitting some digits. 4. Simplification is not usually required. If you give a decimal approximation as your answer, use the symbol and round to 3 decimal places. Circle or box your answer! 5. Show steps. Don’t make leaps of logic. You may use and symbols as transitions (e.g., “f diff. at c (given) f cont. at c”), but for the most part, simply write one thought on each line. 6. Don’t waste time erasing large areas. Just mark them out with a quick X. 7. Avoid using the word it.